Теория и реализация языков программирования
LL(k)-грамматики
Определение. КС-грамматика G = (N, ?, P, S) называется LL(k)-грамматикой для некоторого фиксированного k, если из
(1)

(2)

и
FIRSTk(x) = FIRSTk(y), вытекает, что ? = ?.
Говоря менее формально, G будет LL(k)- грамматикой, если для данной цепочки


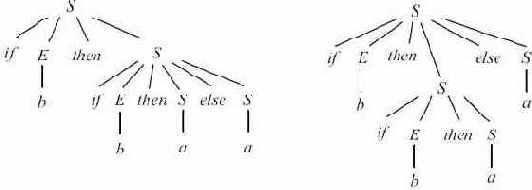
Рис. 4.4.
начинающейся с ? и продолжающейся упомянутыми k терминалами.
Грамматика называется LL(k)-грамматикой, если она LL(k)-грамматика для некоторого k.
Пример 4.7. Рассмотрим грамматику G = ({S, A, B}, {0, 1, a, b}, P, S), где P состоит из правил
S



Здесь L(G) = an0bn | n





Обращаясь к точному определению LL(k)-грамматики, положим ? =


соответствуют выводам (1) и (2) определения. Первые k символов цепочек x и y совпадают. Однако заключение ? = ? ложно. Так как k здесь выбрано произвольно, то G не является LL-грамматикой.