Абсолютно незацикленные атрибутные грамматики

Обозначим IOx ориентированный граф, вершинами которого являются атрибуты символа X и из вершины b идет дуга в вершину a тогда и только тогда, когда в атрибутной грамматике AG существует такое поддерево с корнем X, что в графе зависимостей этого поддерева существует путь из b в a. Через

обозначим граф Dp[IOX1, ..., IOX n p].

Атрибутная грамматика называется абсолютно незацикленной (ANC), если ни один из графов D не содержит ориентированных циклов [6].

Абсолютно незацикленные атрибутные грамматики образуют собственный подкласс незацикленных атрибутных грамматик.

Пример B.1. Незацикленная атрибутная грамматика, не являющаяся абсолютно незацикленной (рис. B.1.).

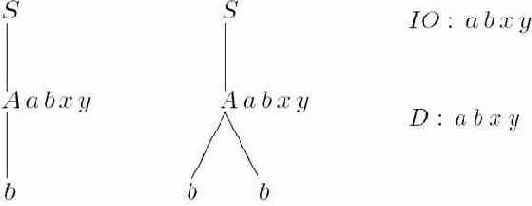
Рис. B.1.

Эта грамматика порождает всего два слова b и bb. Каждое из двух деревьев порождает незацикленные графы зависимостей, однако грамматика не является абсолютно незацикленной. Происходит это от того, что зависимости, реализуемые в разных деревьях, "накладываются" на один граф IO.

Для построения графов IO имеется простой полиномиальный алгоритм:

Алгоритм B.3. Построение графов IO атрибутной грамматики AG.

Поскольку этот алгоритм полиномиален и задача определения наличия ориентированных циклов в графе также полиномиальна, справедлива следующая теорема:

Теорема B.9. Задача определения, является ли данная атрибутная грамматика абсолютно незацикленной, полиномиальна по длине атрибутной грамматики. Абсолютно незацикленные атрибутные грамматики интересны тем, что для них имеется полиномиальный алгоритм планирования визитов.

Обозначим через A(p) множество атрибутов символов синтаксического правила p. Рассмотрим атрибутированное дерево t в AG и некоторую его внутреннюю вершину n, в которой применено правило вывода p. В каждый момент времени в процессе вычисления атрибутов дерева t каким- либо алгоритмом вычисления какие-то атрибуты из A(p) вычислены, а какие-то нет. Назовем состоянием правила, примененного в дереве вывода, множество вычисленных атрибутов символов, входящих в это правило.
Начальным состоянием для каждого правила является множество {a<k> j Xk

T}.

План - это последовательность инструкций вида fpa<k> или V ISIT (k, I), где

, если k - номер символа правой части правила p. I называется входным множеством. План всегда завершается инструкцией

- перевести правило p в состояние A. Инструкция fpa<k> вычисляет атрибут a<k>, V ISIT(k, I) осуществляет визит в поддерево k-го символа правой части со значениями наследуемых атрибутов I этого символа, инструкция S изменяет состояние правила.

Обозначим Dpa<k> - множество аргументов семантического правила fpa<k>. Будем говорить, что семантическое правило f готово к вычислению в состоянии A правила p, если a<k>

A, но

.

Если p : X0

X1 ... Xnp и правило p находится в состоянии A, то результатом k-го поддерева, k

[1, np], будем называть множество {a<k> j a<k>

A, a

S(Xk) и для каждого i<j>, для которого есть дуга из i<j> в a<k> в IOXk, i<j>

A} (предполагается, что у каждого нетерминала есть хотя бы один синтезируемый атрибут).

Планирование осуществляется нижеследующим алгоритмом. Результат работы алгоритма заносится в двумерный массив EVAL, одним входом в который служит состояние правила, другим - входное множество. Строка - это строка инструкций Stv - вектор состояний правил; он передается как аргумент процедуре PLAN, затем дублируется внутри процедуры PLAN и обращение к PLAN меняет значение своего аргумента в точке вызова (что обозначено знаком var перед параметром Stv процедуры PLAN). Если для некоторого элемента таблицы EVAL в процедуре PLAN начато построение плана, то этот элемент метится значком @, чтобы избежать бесконечной рекурсии. Будем говорить, что функция f готова к вычислению, если все еe аргументы определены, но атрибут, который она вычисляет не определeн.

Алгоритм B.4. Построение планов для каждого возможного состояния каждого правила.

var EVAL : array[состояние, входное множество] of строка; St : array [1 .. P] of состояние; fP - число синтаксических правил} procedure PLAN( p, I, var Stv); {p - номер синтаксического правила, I - входное множество, Stv - вектор состояния правил} var S : строка {строящийся план}; LStv : array [1 ..

p] of состояние; {локальный вектор состояния правил} A : set of атрибут;{ состояние правила p} stop: boolean; begin if (EVAL [Stv[p], I] пуст) then A := I [ Stv[p], s := пусто , LStv := Stv; stop := false, EVAL [Stv[p], I] :='@' repeat if (

fpa<k> готовая к вычислению) then s := s || fpa<k>, A := A + a<k> else if (

поддерево k, результат Y которого не пуст) then s := s || V ISIT(k, I(Xk)

A), A := AUY ; for pi : Xk

u do PLAN(pi, I(Xk)

A, LStv) {в этой точке меняется значение LStv[pi]} end else stop := true end end until stop; EVAL [Stv[p], I] := s || st(A), Stv := A {Stv[p] меняется в точке вызова} end end; {тело программы} begin for I := 1 to p do St[i] := множество атрибутов терминалов правила i; PLAN({}, {}, St) end end.

Вычисление атрибутов на дереве t заключается в выполнении построенных планов в соответствии с изменениями состояний правил и осуществляется следующей программой:

begin каждое правило дерева t перевести в начальное состояние, определяемое множеством атрибутов терминалов; V ISIT(корень, {}) end.

Содержание раздела