Теория и реализация языков программирования
Многопроходные грамматики
Пусть на последовательность визитов наложено такое ограничение, чтобы они образовали последовательные обходы дерева разбора либо сверху-вниз слева-направо, либо сверху- вниз справа-налево.
Атрибутная грамматика называется чистой k- проходной в обоих направлениях, если существует такая последовательность из k обходов <d1 ... dl> (каждое di - либо справа-налево, либо слева-направо), что атрибуты любого дерева вывода могут быть вычислены в результате выполнения этой последовательности обходов [5].
Атрибутная грамматика называется чистой многопроходной в обоих направлениях (PBD), если она является чистой k-проходной в обоих направлениях для какого-нибудь k.
Пример B.3. Существуют атрибутные грамматики, не являющимися чистыми многопроходными ни для какого k ( рис. B.3).
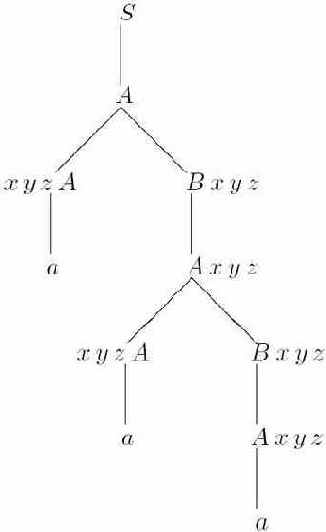
Рис. B.3.
Число необходимых проходов в этом примере зависит от глубины дерева и может быть сколь угодно большим.
Очевидно, что грамматика примера рис. B.1 не является чистой многопроходной и нетрудно видеть, что грамматика примера рис. B.1 является абсолютно незацикленной.
Теорема B.14. Задача определения того, является ли произвольная атрибутная грамматика чистой многопроходной в обоих направлениях, зависит экспоненцально от размера атрибутной грамматики.
Атрибутная грамматика называется чистой k-проходной слева-направо, если атрибуты любого дерева вывода в ней могут быть вычислены за k обходов дерева вывода слева- направо [2, 5].
Атрибутная грамматика называется чистой многопроходной слева-направо (PLR), если она является чистой k-проходной слева-направо для какого-нибудь k.