Простые многовизитные атрибутные грамматики

Атрибутная грамматика называется простой k-визитной, если для каждого нетерминала X

V существует разбиение A1(X), ... , Am(X) множества атрибутов A(X), где m

[1, k] и m может зависеть от X, то есть m = m(X), такое, что для любого дерева вывода t слова из G существует вычислительная последовательность, при которой для любого вхождения X в t все атрибуты Aj(X) вычисляются при выполнении j-го визита в поддерево c корнем X для всех j

[1;m(X)] [7].

Атрибутная грамматика называется простой многовизитной (SMV ), если она является простой k-визитной для какого-нибудь k.

Существуют абсолютно незацикленные атрибутные грамматики, не являющиеся простыми многовизитными.

Пример B.2. Здесь атрибуты a и b символа A левого поддерева вычисляются на первом визите, а x и y - на втором. Для символа A правого поддерева наоборот - атрибуты x и y вычисляются на первом визите, a и b - на втором ( рис. B.2).

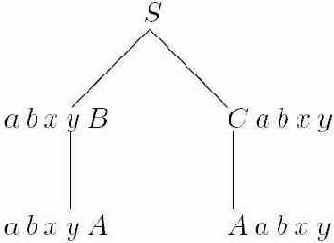
Рис. B.2.

Теорема B.10. Всякая простая k-визитная грамматика является абсолютно незацикленной [7].

Теорема B.11. Задача определения того, является ли произвольная атрибутная грамматика простой многовизитной, NP-полна [7]. Мало того, NP-полна даже задача определения простой 2-визитности [7] Если для каждого символа дано разбиение его атрибутов по визитам, то алгоритм вычисления атрибутов дерева принимает следующий вид:.

Алгоритм B.5. Вычисление атрибутов в простой многовизитной грамматике.

procedure визит_в_поддерево(n, i); begin вычислить наследуемые атрибуты I(Xn); визит_в_поддерево (nj1, ij1); ... визит_в_поддерево (njm, ijm); вычислить синтезируемые атрибуты S(Xn) end; beginforj := 1tok(Xr)do визит_в_поддерево (r, j){r - корень} end:

Содержание раздела