Введение в теорию программирования. Объектно-ориентированный подход
Концепция наследования и ее реализация в языке C#
Формализуем понятие наследования и обсудим его значение для объектно-ориентированного подхода к программированию. Напомним, что эволюция теоретических основ наследования была рассмотрена во вступительной лекции.
Под наследованием в дальнейшем будем понимать свойство производного объекта сохранять поведение родительского объекта. Под поведением будем иметь в виду для математического объекта его атрибуты и операции над ним, а для языкового объекта ООП - поля и методы.
Таким образом, применительно к языку программирования концепция наследования означает, что свойства и методы базового класса равно применимы к производным от него классам. Заметим, что дочерний объект не обязательно наследует все без исключения атрибуты и операции родительского, а лишь некоторые из них. Такой подход характерен как для классов объектов в целом, так и для отдельных их конкретизаций, или, иначе, экземпляров.
Теоретическая концепция наследования удовлетворительно моделируется посредством отношения (или, точнее, иерархии) частичного порядка. Существует целый ряд формализаций наследования, но наиболее адекватными и концептуально ясными являются графические модели. Среди них следует выделить уже упомянутые ранее подходы: фреймовую нотацию Руссопулоса и диаграммы Хассе.
Отношение частичного порядка обладает следующими теоретически интересными и практически полезными свойствами.
Во-первых, оно является рефлексивным, т.е. любой объект языка программирования или формальной модели предметной области находится в отношении частичного порядка с самим собой. Формальная запись свойства рефлексивности для отношения частичного порядка ISA выглядит следующим образом:

Другой важной особенностью отношения частичного порядка является транзитивность. Суть транзитивности состоит в том, что если существует цепочка из (трех) объектов, связанных отношением частичного порядка, то первый и последний элементы этой цепочки можно связать тем же отношением. Это свойство гарантирует построение на множестве графа отношения частичного порядка в виде "решетки".
Формальная запись свойства транзитивности для отношения частичного порядка выглядит следующим образом:


Наконец, еще одним фундаментальным свойством отношения частичного порядка как модели наследования является антисимметричность. Это свойство разрешает наследование только в одном направлении (и запрещает его в противоположном). Формальная запись свойства антисимметричности для отношения частичного порядка выглядит следующим образом:


По завершении исследования свойств отношения частичного порядка, перейдем к рассмотрению формализаций, моделирующих наследование. Проиллюстрируем графическую интерпретацию отношения частичного порядка на примере фреймовой нотации Руссопулоса. Рассмотрим следующий фрейм (рис. 19.1), который связывает отношением частичного порядка понятия "сущность" (THING), "юридическое лицо" (LEGAL.PERSON), "учреждение" (INSTITUTION), "работодатель" (EMPLOYER), "кадровое агентство" (RECRUITER), "физический объект" (PHYSICAL.OBJECT), "одушевленный объект" (ANIMATE.OBJECT), "человек" (PERSON), "мужчина" (MALE.PERSON) и "женщина" (FEMALE.PERSON).
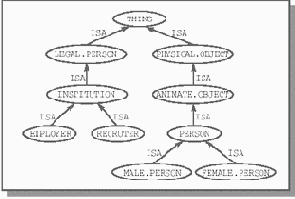
Рис. 19.1. Пример фрейма.
Как видно из структуры фрейма, понятия (или, точнее, концепты) изображены в овалах. Направленные ISA-дуги соединяют понятия, образуя иерархию с направлением в сторону увеличения уровня общности (абстракции), например, от понятия "мужчина" к понятию "сущность". Рефлексивные и транзитивные дуги опущены для удобства восприятия; их без труда можно восстановить. Ориентированность дуг характеризует антисимметричность отношения частичного порядка: любая из дуг может иметь только одну стрелку со стороны увеличения уровня абстракции.
Другой продуктивной формализацией, моделирующей, в частности, наследование, является диаграмма Хассе. Проиллюстрируем использование диаграмм Хассе для графической интерпретации отношения между элементами класса или домена (см.рис. 19.2).
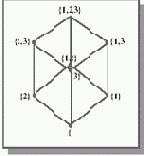
Рис. 19.2. Пример диаграммы Хассе.
Диаграмма Хассе состоит из точек, которые представляют элементы множества (точнее, домена или класса), а также из соединяющих их линий, которые представляют собой отношения между элементами класса или домена (в данном случае интерпретируется отношение частичного порядка).
Данный пример иллюстрирует отношение IS IN ("является подмножеством") между множествами {}, {1}, {2}, {3}, {1,2}, {1,3}, {2,3} и {1,2,3}.
Заметим, что в случае графической интерпретации отношения частичного порядка с помощью диаграммы Хассе свойство антисимметричности рассматриваемого отношения было бы отображено в явном виде.