Геометрические преобразования и привязка изображений

          Многие задачи тематического дешифрирования сводятся к взаимному сопоставлению между собой изображений, сформированных с помощью датчиков различных физических полей. Ярким примером может служить развитие дистанционных методов контроля природных ресурсов и динамики экосистем (так называемого мониторинга), что сводится к сопоставлению снимков одной и той же территории, полученных в разное время и/или с помощью различных датчиков. Чаще всего используются оптическое, радиолокационное, радиотепловое, магнитное и другие поля. Совместное использование различных физических полей требует предварительной обработки соответствующих им изображений, например, с целью перевода изображений в одну спектральную область.

На практике изображения одного и того же объекта или участка местности, полученные в разное время или с помощью различных датчиков, могут значительно различаться один от другого. Отсюда вытекает ряд важных задач привязки, а также точной взаимной геометрической и амплитудной коррекции для последующего совместного анализа.


В любом случае это требует установления соответствия между элементами исходных изображений, что сводится к выделению так называемых опорных

(по другому, реперных или сопряженных) точек на изображениях, по которым можно осуществить координатную привязку снимков с одновременной геометрической коррекцией. (Точки на двух изображениях называются сопряженными, если они являются образами одной точки сцены [5.1, гл.13]). Например, аэрокосмический компьютерный мониторинг предполагает наличие дискретного по времени  наблюдения с небольшим временным интервалом, и поэтому, когда движущаяся камера фиксирует яркостный образ наблюдаемого объекта (оптическую поверхность) в виде последовательности изображений, то этот образ от снимка к снимку  деформируется вследствие перспективных искажений и изменения положения камеры. Геометрия соответствующих деформаций моделируется проективными преобразованиями, которые составляют более обширный класс, нежели известные  преобразования евклидовой геометрии (достаточно сказать, что длины и углы  в проективной геометрии не сохраняются, а параллельные линии могут пересекаться! [5.12]).

Восстановление пространственного рельефа по стереоснимкам приводит к проблеме идентификации: установления точного координатного (поточечного) соответствия элементов стереоизображений. Решение этой задачи состоит в выделении пар реперных фрагментов и  оценивании параметров «расхождения» соответственных точек (это именуется в стереофотограмметрии бинокулярной диспарантностью), по которым можно восстановить функцию геометрического преобразования  и оценить поверхность трехмерной сцены (рельеф)[5.5].

5.1. Геометрические преобразования на плоскости и в пространстве

Геометрия является математическим базисом для решения многих задач машинного зрения и обработки изображений и содержит множество подобластей. Здесь мы рассмотрим лишь некоторые в охарактеризованном выше контексте привязки, преобразования и совмещения разновременных изображений одного и того же объекта.



При изучении геометрических преобразований плоских изображений (то есть относящихся к двумерному случаю - 2D), будем предполагать, что мы работаем в евклидовом пространстве, где имеется ортонормированная декартова система координат, в которой координатные оси взаимно ортогональны, а соответствующие им единичные отрезки имеют одинаковую длину. Тогда каждой точке изображения ставится в соответствие упорядоченная пара чисел  декартовых координат: их можно интерпретировать как двумерный вектор , геометрически представляемый отрезком прямой линии из точки  в точку .

Двумерные преобразования на плоскости мы будем интерпретировать как движения точек по отношению к фиксированному базису (а не как изменение базиса, оставляющее точки неподвижными).

В частности, нас особенно будут интересовать линейные преобразования, представляемые матрицами, то есть преобразования, при которых новые координаты точки линейно зависят от старых координат этой точки следующим образом:

                                       .                                                        (5.1)



Линейные преобразования могут быть различного типа, начиная от общего случая произвольных элементов матрицы  вплоть до специальных случаев, когда на элементы матрицы накладываются те или иные ограничения. Интуитивно ясно, что каждому линейному преобразованию (или движению) на плоскости всегда найдется обратное, переводящее точки в первоначальное положение, и любым двум последовательно выполняемым преобразованиям точек плоскости соответствует некоторое третье преобразование, осуществляющее аналогичную (по результату) операцию. В таком случае принято говорить, что множество всех невырожденных линейных преобразований  является замкнутым или, иначе, формирует группу, называемую здесь общей линейной группой. Интересно отметить, что само множество общих линейных преобразований может быть разбито на замкнутые подмножества или подгруппы. Прежде всего, мы рассмотрим матрицы преобразования, связанные с наиболее важными подгруппами общей линейной (или проективной) группы, а именно евклидову подгруппу, а также подгруппы подобия и аффинную.


Это является следствием того, что евклидова геометрия (также как и аффинная) в действительности является подмножеством выше упомянутой нами проективной геометрии.

5.1.1. Точки и прямые линии на плоскости - двойственность описаний

 Прямая линия на плоскости, как известно из аналитической геометрии, состоит из всех точек, удовлетворяющих уравнению

.

Пусть две точки имеют координаты  и  соответственно. Каково уравнение линии, соединяющей их? Ясно, что поскольку линия проходит через эти точки, то она должна удовлетворять двум уравнениям

,

.

Данную систему из двух уравнений можно легко разрешить относительно неизвестных значений  и  и получить соответствующие выражения

  .

С другой стороны, предположим, что имеются две линии, и нужно найти их точку пересечения . Но две прямые должны соответствовать уравнениям

,

.

Отсюда для координат точки пересечения  получаем соотношения, аналогичные вышеприведенным соотношениям для параметров линии :

  .

Здесь просматривается очень важная симметрия или двойственность

между проблемами пересечения двух прямых и (с другой стороны) линии, проходящей через две заданные точки. Координаты (параметры) пары линий и координаты пары точек в обоих случаях входят в формулы одинаковым образом. Далее мы увидим, что отмеченная двойственность распространяется и на другие соотношения между геометрическими объектами.

Имеется ряд проблем, связанных со специальными соотношениями выделенных пар точек и прямых. Предположим, что координаты двух точек отличаются лишь скалярным множителем: . Это означает, что  и параметры прямой, соединяющей выделенные точки, определить невозможно. Прямая линия в данном случае проходит через начало координат (0,0), что собственно и создает проблему. Здесь нельзя непосредственно использовать уравнение прямой линии  (проходящей через начало координат). Аналогичная проблема возникнет, когда  мы попытаемся (формально, из приведенных выше уравнений) найти точку пересечения двух параллельных прямых, когда .



5.1.2. Однородные координаты

  Для преодоления отмеченных проблем описания геометрических объектов, а также для решения задач преобразования 3D-пространства и 2D-плоскости  в единообразном (матричном) виде вводится формализм так называемых однородных координат. Однородными координатами служат тройки чисел  (одновременно не равные нулю), связанные с обычными  координатами точек плоскости соотношением:

, так что . Совершенно очевидным свойством однородных координат является эквивалентность пары однородных векторов, если один в другой переводятся посредством скалярного множителя

.

Поскольку скалярный множитель  произвольный, то однородные координаты в действительности представляют линию, проходящую через начало координат в евклидовом пространстве. Прямые линии на плоскости также можно представить 3-векторами в однородных координатах:

, где  - произвольный скалярный множитель.

Видно, что, как и для двух точек, однородные координаты двух линий эквивалентны, если отличаются лишь общим скалярным множителем. Однородные точки , лежащие на однородной линии  определяются уравнением

 или .

Таким образом, точки и линии имеют здесь одинаковые представления. Нетрудно заметить, что прямым, проходящим через начало в данном представлении соответствует значение . Двойственным образом, точка пересечения двух параллельных прямых, лежащая в бесконечности, имеет множитель .

5.1.3. Евклидовы преобразования

 Сцену иногда можно рассматривать как твердое тело, когда взаимные деформации элементов сцены в трехмерном пространстве не допускаются. Аналогично и плоскость иногда можно считать жесткой (недеформируемой). Жестким движениям плоскости соответствует евклидова подгруппа, содержащая лишь преобразования сдвига и поворота (рис.5.1), математически записываемых в векторно-матричной форме как

               ,                                   (5.2)

с матрицей поворота на угол  вида и вектором трансляции (сдвига) .



При помощи троек однородных координат и матриц третьего порядка можно описать любое линейное преобразование плоскости. Действительно, введением дополнительной единичной компоненты уравнение (5.2) можно переписать следующим образом:

                                                                (5.3)

Отметим далее, что два последовательно проведенные жесткие движения плоскости могут быть представлены единственным движением:



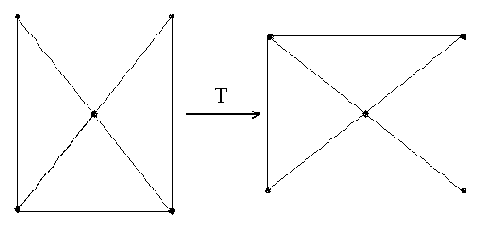
Рис.5.1. Действие евклидова преобразования на пять точек плоскости

(сдвиг, поворот)

                   (5.4)

Комбинация двух последовательных вращений  и  очевидно сводится к вращению . Кроме того, выбором вращения  и сдвига  такое (второе) жесткое движение переводит точки плоскости в первоначальное положение. Отмеченной парой свойств, собственно говоря, и характеризуется группа, а класс матриц со структурой вида (5.3) известен как евклидова группа преобразований. (Она является, естественно, частным случаем линейных преобразований у которых матрицы произвольные. Эти матрицы невырожденные и формируют общую линейную группу преобразований или проективную группу.) Интересно, что матрицы вращения сами по себе формируют так называемую ортогональную подгруппу с замечательным свойством , где - единичная матрица.

5.1.4. Аффинные преобразования

 

 Если матрицу вращения в (5.2) заменить  общей невырожденной матрицей , то получим преобразование

                                                        (5.5)

или, в матричном виде

                           ,                  



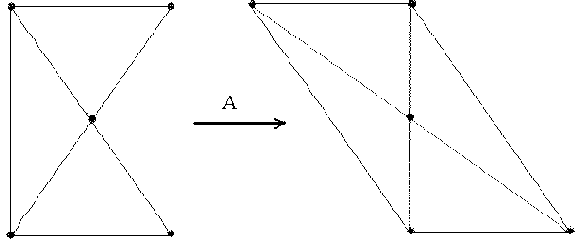
а)

              

б)

Рис.5.2.

а) действие аффинного преобразования на пять точек (сдвиг, поворот, изменение масштабов вдоль осей, косоугольность с сохранением  параллельных линий);

б) исходное изображение (слева) и его аффинно-преобразованная копия  (справа);параметры аффинного преобразования:

и в однородных координатах

                                           (5.6)



Здесь также предполагается, что определитель матрицы преобразования не равен нулю:     

Уравнения (5.5),(5.6) определяют общую форму записи хорошо известного аффинного преобразования (смотрите рис.5.2). Любое аффинное преобразование имеет обратное, которое также является аффинным. Произведение прямого и обратного преобразований дает единичное преобразование, оставляющее все на месте.  Аффинное преобразование является самым общим взаимно однозначным отображением плоскости на плоскость, при котором сохраняются прямые линии. Сохраняются также отношения длин отрезков, лежащих на одной прямой (или на параллельных прямых), и отношения площадей фигур. Параллельные прямые переходят в параллельные.

 В аффинных преобразованиях плоскости особую роль играют несколько важных частных случаев, имеющих простой и наглядный геометрический смысл, а также хорошо прослеживаемые геометрические характеристики [5.4,гл.15].

1.Растяжение (сжатие)

вдоль координатных осей, задаваемое в виде:



Растяжению вдоль соответствующей оси соответствует значение                       масштабного  множителя большего единицы. В однородных координатах матрица растяжения (сжатия) имеет вид

.

2.Поворот вокруг начальной точки на угол , описываемый формулой:



Матрица вращения (для однородных координат)

.

3.Перенос, задаваемый простейшими соотношениями:



Матрица переноса имеет вид

.

4.Отражение (относительно какой либо из осей, например оси абсцисс) задается при помощи формулы:



Матрица отражения, соответственно

.

Из курса аналитической геометрии хорошо известно, что любое аффинное преобразование (5.5) всегда можно представить в виде композиции последовательно выполняемых простейших преобразований означенного вида. Более того, суперпозиция аффинных преобразований также является аффинным преобразованием. Ясно, что аффинные преобразования образуют аффинную группу. В частности подгруппой аффинной группы преобразований является группа подобия (содержащая преобразования сдвига, поворота и изменения масштаба):





В то же время аффинная группа является подгруппой общей линейной (проективной) группы, а евклидова группа является частным случаем аффинной группы преобразований. Поэтому все отмеченные преобразования формируют иерархию в том смысле, что верно соотношение для их взаимной соподчиненности

евклидово преобразование  аффинное  проективное преобразование.

Зная параметры аффинного преобразования, можно вычислить непосредственно и параметры обратного преобразования



решив систему уравнений (5.5) относительно :



Если параметры таковы, что , то данное аффинное преобразование имеет неподвижную точку :



Заметим, что при  начало координат и будет являться неподвижной точкой.

 

5.1.5. Проективные преобразования

Как выше уже было сказано, общими линейными преобразованиями  (в представлении однородными координатами)

                                                                                 (5.7)

формируется группа проективных преобразований (рис.5.3). При представлении в обычных координатах, очевидно соотношение (5.7) будет иметь нелинейный вид, связанный с перенормировкой

.

Проективные преобразования, в общем-то, не сохраняют параллельности линий. Свойством, сохраняющимся при проективном преобразовании, является так называемая коллинеарность точек: три точки, лежащие на одной прямой (то есть коллинеарные), после преобразования остаются лежать на одной прямой(см.рис.5.3). Поэтому обратимое проективное преобразование принято называть еще

коллинеацией.

Проективное преобразование связано с отображением трехмерной визуальной информации на двумерную плоскость. С математической точки зрения удобно рассматривать мир, включенным в трехмерное проективное пространство , а плоскость изображения, включенной в проективное пространство размерности два -  . Точки на трехмерной сцене и на изображении представляются в проективных пространствах как векторы в однородных координатах.

Проективное преобразование из  в (перспективная проекция), отображающее евклидову точку сцены  в точку изображения и выраженное в однородных координатах, задается в виде:



=.                (5.8)



а)

 

б)

в)	г)

Рис.5.3.

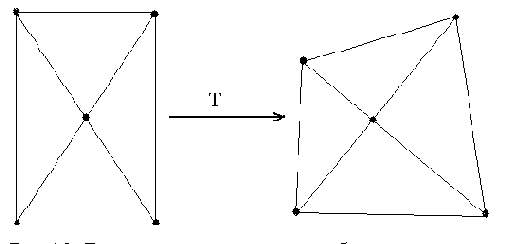
а) действие проективного преобразования на пять точек плоскости;

б) исходное изображение; в) и г) проективно преобразованные образы; параметры проективного преобразования соответственно:



и



Однородные координаты векторов проективного пространства  и проективной плоскости соотносятся с неоднородными (евклидовыми) координатами векторов  и заданным выше образом:   и  .

Проективная геометрия составляет математический базис машинного зрения и компьютерной графики.  Основные области применения связаны с описанием как процесса формирования изображений, так и их инвариантного представления , а именно: калибровка регистрирующей камеры, анализ движения по серии изображений, распознавание образов, реконструкция сцен по стереоснимкам, синтез изображений,  анализ и восстановление формы по полутонам. Полезно отметить тот факт, что композиция двух перспективных проекций не является с необходимостью перспективной проекцией, но определяет проективное преобразование; то есть (как мы знаем) проективные преобразования формируют группу, в то время как перспективные проекции - нет.

 В связи с этим напомним, что изображение объектов на снимке, сформированном регистрирующей камерой, связано с чрезвычайно важной геометрической операцией - проектированием при помощи пучка прямых, поскольку каждая 2D точка является проекцией множества  3D точек вдоль некоторого направления («луча проектирования») в плоскость снимка (рис.5.4). Предположим, что плоскость снимка камеры в системе координат определяется соотношением .  Простая геометрия показывает,

что если расстояние от плоскости изображения до центра проекции равно , то координаты элементов изображения  соотносятся с пространственными координатами объекта следующим образом

                            .                                                 (5.9)

Это нелинейные уравнения. Они могут быть сделаны линейными введением однородных координат.


Заметим, что луч, проходящий через 2D точку , является направляющим вектором прямой, соединяющей точки   и . В то же время 3D точка  также лежит на этом луче (и представляет его). Припроизвольном (пробегающем всевозможные значения) получим координаты всех 3D точек на этом луче, соответствующих единственной точке на изображении в плоскости . По существу, каждая точка на изображении определяет луч, идущий от сцены в начало координат. Следовательно, однородные координаты точки (на снимке) в действительности представляют (и определяют) линию, проходящую через начало в евклидовом трехмерном пространстве . Такой набор всевозможных линий, проходящих через начало и формирует проективное 2D-пространство  в плоскости . (Можно, конечно, положить фокусное расстояние , поскольку различным значениямсоответствует разный масштаб изображения). В однородных координатах уравнения (5.9) естественно имеют вид (5.8)



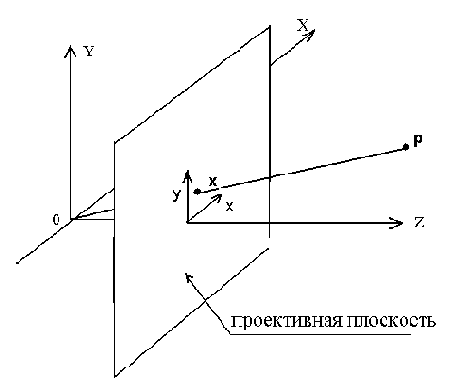
Рис.5.4. Перспективная проекция

                                                  (5.9)

 Замечание. При , 3D точка  , в общем-то, определяет линию, параллельную плоскости  ,  не имеющую с ней точек пересечения и, следовательно, не имеет соответствия с какой-либо конечной точкой изображения.  Такие линии или однородные векторы могут, тем не менее, иметь смысл, если считать, что соответствующая им точка  удаляется на бесконечность в направлении, задаваемом этими координатами:

.

Мы можем добавить все такие точки к проективной плоскости. Эти точки называются «идеальными» или точками на бесконечности. На изображениях проективной плоскости добавленные точки на бесконечности формируют «линию горизонта» (см. рис.5.5). Существует разделение идеальных точек, обусловленное различными направлениями на плоскости; например, точки (1,0,0) и (0,1,0) связаны с горизонтальным и вертикальным направлениями (осями координат) соответственно. Можно также сказать, что все идеальные точки лежат на линии, называемой «идеальной линией» или линией на бесконечности, которая рассматривается, тем не менее, как и обычная линия.


Идеальная линия представляется в виде (0,0,1).

Определение. Проективная плоскость  является аффинной плоскостью с присоединенными идеальной линией и множеством идеальных точек, которые не отличаются от обычных  линий и точек [5.12]. (Аффинная плоскость, естественно, состоит из  тех же точек, что и евклидова плоскость. Различие состоит в том, что в первой допускаются неоднородное масштабирование и косоугольность.)



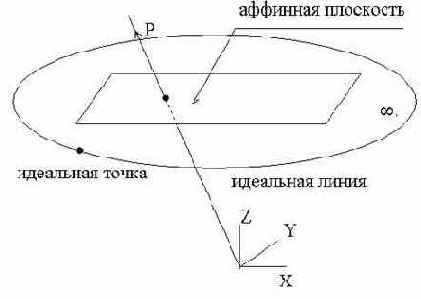
Рис.5.5. Проективная плоскость = аффинная плоскость + идеальные точки

(идеальная линия)

Замечание. Найдем пересечение двух прямых  и . Несложные вычисления показывают, что однородные координаты точки пересечения    равны . Последняя формула легко запоминается, поскольку есть не что иное, как векторное произведение: . Если эти две прямые линии параллельны, то есть , то точка пересечения существует (идеальная точка!) и равна . Двойственным образом, задавая две точки  и , можно непосредственно найти прямую, проходящую через них: .

         

Таким образом, идеализация процесса формирования изображения камерой может быть представлена как перспективная проекция из в . Допустим, что 3D координаты точек объекта известны. Тогда, зная элементы матрицы , относящиеся к данному проективному преобразованию, точки пространственного объекта можно связать с соответствующими им координатами на снимке в виде (5.8)

 

         =.                       (5.10)

Очевидно, что неизвестный масштабный множитель определяется как

,

так что координаты изображения объекта имеют вид отношения

,

(5.11)

.

Пусть координаты характерных элементов изображения объекта соотнесены с пространственными координатами точек объекта и требуется вычислить элементы матрицы (то есть осуществить так называемую  калибровку камеры, см. главу 6). По крайней мере 6 точек объекта нужно идентифицировать для этого на снимке(, поскольку элементы матрицы определены с точностью до масштабного множителя (только лишь отношения элементов  значимы) и существует 11 степеней свободы (неизвестных параметров).


Обычно же требуется большее число точек, так как измерения сопровождаются помехами и оптимальное решение, минимизирущее их влияние на результат, находится методом наименьших квадратов.

Проективным базисом  на плоскости является множество из 4 точек, таких, что любые три из них не лежат на прямой. Соответственно, матрица, сформированная вектор-столбцами однородных координат любых 3 точек, должна иметь полный ранг. Легко проверить, например, что точки формируют так называемый  канонический базис. В соответствии с приведенным выше замечанием, канонический базис содержит точки на бесконечности вдоль каждой координатной оси , начало и единичную точку . Очевидно, что коллинеация на :  целиком характеризуется геометрически ее действием на точки базиса.

Элементы матрицы определены с точностью до масштабного множителя, и из них лишь восемь значений независимы. Поэтому, поскольку каждая точка содержит две независимых координаты, то четыре пары сопряженных точек (на двух снимках) позволяют определить .

Мы знаем, что аффинная плоскость, в отличие от проективной плоскости, не содержит идеальных точек. Тогда точка  должна быть трансформируема в точку  для произвольного масштабного множителя :

,

что влечет .   Матрица  аффинного  преобразования  имеет  вид

, и здесь содержится лишь шесть независимых параметров, поскольку масштаб также не важен.

 

5.1.6. Полиномиальное преобразование

Выше мы привлекли к рассмотрению геометрических преобразований, в общем-то, идеализированную модель камеры. В действительности формирование изображений сопровождается различного рода нелинейными искажениями (типа оптической дисторсии линзы). Приведение текущих снимков друг к другу или к некоторому эталонному в таком случае можно осуществить лишь нелинейной функцией преобразования. Кроме того, неравномерность движения носителя регистрирующей камеры также приводит к тому, что на практике геометрические искажения снимков не устраняются аффинным преобразованием координат элементов снимка.


Поэтому привлекают полиномиальную аппроксимирующую функцию преобразования (рис.5.6)

                    ,

                    ,                  (5.12)   

где  - координаты точек эталонного снимка, - соответствующие им координаты на текущем (сопоставляемом) снимке.   

 

Рис.5.6. Действие билинейного геометрического преобразования на исходный снимок; параметры преобразования:

              

 

 

5.1.7. Оценивание параметров преобразования

 

 Параметры линейных и нелинейных преобразований (5.2),(5.5),(5.12)  устанавливаются по парам взаимно соответствующих реперных точек, идентифицируемых в процессе поиска (см. далее). После этого каждой точке  эталонного снимка  ставится в соответствие точка  текущего снимка. Будем считать, что точки цифрового изображения (пикселы) представлены на дискретной  решетке с постоянным шагом так,  что их целочисленные координаты имеют вид . Коэффициенты  выбирают таким образом, чтобы минимизировать среднеквадратичную ошибку аппроксимации фактически «наблюдаемых» координат  их полиномиальной оценкой из (5.12) для набора заданных узловых точек  Координаты в плоскости наблюдаемого (текущего, или контролируемого) изображения удобно выразить в виде векторов

,    .

Аналогично коэффициенты полиномов можно представить в векторной форме

,    .

Среднеквадратическую ошибку оценивания можно записать в компактной матричной форме

,                        (5.13)

где                                       .                                   

Оценки наименьших квадратов (минимизирующих среднеквадратическую ошибку ) находятся приравниванием производных квадратичной формы (5.13) по векторам параметров  и  нулю, в результате чего приходим к соотношениям:

                               .                                   (5.14)

Следовательно, искомые оценки имеют вид

                           ,.                             (5.15)



При больших значениях  регрессионная матрица , соответствующая (5.12), становится неустойчивой, что приводит к большим ошибкам в определении коэффициентов преобразования. Одним из способов уменьшения этого эффекта является использование полиномов Чебышева. Полиномиальное преобразование (5.12) в этом случае представляется как

                                     (5.16)

                                     (5.17)

где -попарно ортогональные на заданном множестве точек ортогональные многочлены Чебышева, получаемые из последовательности методом ортогонализации Грама-Шмидта [5.3, гл.20]. Ортогональные многочлены до третьей степени имеют вид



Коэффициенты снова выбирают таким образом, чтобы минимизировать среднеквадратичную ошибку аппроксимации фактически «наблюдаемых» координат  их полиномиальной оценкой из (5.16),(5.17) для набора заданных узловых точек

Пользуясь этой методикой, можно без труда вычислить коэффициенты  по методу наименьших квадратов (аналогично формулам (5.13)-(5.15)), где регрессионная матрица имеет вид

            .                   (5.18)

5.2. Восстановление изображения в преобразованных

 координатах

После оценивания параметров геометрического преобразования встает задача собственно геометрической коррекции или, по другому, восстановления изображения в преобразованных координатах.

Будем считать, что заданы два снимка (и ) одной и той же местности, полученные с некоторыми отклонениями точек съемки и условий     



Рис.5.7. Вычисленные координаты  (выделены серым тоном), наложенные на исходную дискретную целочисленную решетку

освещенности.  Вследствие этого    изображения на снимках отличаются друг от друга геометрическими  искажениями. Будем также считать, что на изображениях выделены сопряженные точки, по которым произведено оценивание параметров геометрического преобразования. Зная коэффициенты линейного (или полиномиального) преобразования, можно вычислить в плоскости корректируемого изображения координаты всех точек , соответствующие точкам с целочисленными координатами на эталонном снимке  (рис.5.7).



Восстановив уровни яркости наблюдаемых элементов в вычисленных точках на корректируемом снимке, то есть осуществив «передискретизацию», полученные значения также можно поместить на дискретном растре размером , приведя тем самым искаженное изображение в формат эталонного снимка . Поскольку координаты не попадают чаще всего в узлы дискретной решетки (см. рис.5.7), то возникает задача восстановления соответствующего значения яркости по ближайшим отсчетам. Она решается с помощью методов двумерной   интерполяции [5.2, разд.5.3].  Интерполированное непрерывное изображение в плоскости снимка можно описать функцией свертки

                 ,                               (5.19)

где - интерполирующая функция (называемая также интерполяционным ядром), - шаг дискретизации исходного изображения,  - известные отсчеты яркости в точках дискретного растра. Оценка непрерывного изображения позволяет осуществить его передискретизацию на новом множестве точек.

Интерполяционное ядро имеет значительное влияние на численное поведение интерполированных функций. Теоретически оптимальную интерполяцию обеспечивает известная sinc-функция, в одномерном случае имеющая вид

                            ,                                     (5.20)

где  есть ширина полосы частот . Из теоремы отсчетов следует (см. главу 1), что sinc-функция дает наилучшую реконструкцию , если последняя имела ограниченный спектр и была первоначально оцифрована вблизи частоты Найквиста.

Поскольку интерполяция противоположна дискретизации, то интерполирующая функция (5.20) по - существу является идеальным низкочастотным фильтром, вырезающим основной участок ограниченного спектра из множества его повторяющихся копий. Однако этот теоретический метод практически невозможно реализовать в контексте обработки изображений. В частности, ограничение области суммирования в (5.19) приводит к тому, что осцилляции, известные как феномен Гиббса, будут проникать в восстанавливаемый образ . Поэтому на практике используют интерполяционные ядра, реализация которых сопряжена с меньшими трудностями.


В одномерном случае это прямоугольные, треугольные, B-сплайн функции и т.п. [5.2, разд.4.3]. При выборе соответствующего ядра  исходят из соображений как необходимой точности интерполяции, так и вычислительной эффективности. Понятно, что здесь одномерные функции должны быть преобразованы в двумерные функции. Общий подход состоит во введении так называемых «сепарабельных» интерполяционных функций в виде произведения двух одномерных функций. Сепарабельность во многих отношениях достаточно привлекательна в приложениях хотя и влечет неизотропность (за исключением гауссовых функций). Однако данные на квадратной решетке дискретизованы также не изотропно.

С вычислительной точки зрения предпочтителен алгоритм, известный как интерполятор по ближайшему соседу, где значение в точке приписывается равным величине ближайшего отсчета дискретного растра. Этот метод соответствует прямоугольному интерполирующему ядру (рис.5.8). Свертка с прямоугольной функцией в пространственной области эквивалентна умножению сигнала в области частот на sinc-функцию. Последняя является плохим приближением к низкочастотному фильтру, поскольку имеет бесконечное множество боковых лепестков. Алгоритм ближайшего соседа приводит к локальным сдвигам относительно первоначального изображения на величины разностей между вычисленной точкой и ближайшей точкой дискретного растра (то есть вплоть до ).  Треугольное ядро (рис.5.9) в двумерном случае приводит к билинейной интерполяции по четырем ближайшим соседям точки   ,  .



Рис.5.8. Интерполятор по ближайшему соседу с прямоугольным ядром. Справа график модуля Фурье-образа ядра. Пунктирной линией показан идеальный низкочастотный фильтр с частотой среза  .



Рис.5.9. Линейная интерполяционная функция и модуль ее Фурье-образа

(на правом рисунке пунктиром отмечен идеальный низкочастотный фильтр)

Здесь интерполированный сигнал представляется в виде

            ,                 (5.21)

где



Приближение к низкочастотному фильтру здесь еще далеко от идеального, и к тому же производная интерполированного сигнала терпит разрывы в узлах интерполяции (тем не менее формула (5.21) часто применяется на практике, поскольку удовлетворяет одновременно требованиям приемлемой точности и приемлемым затратам вычислительных ресурсов).



Наиболее подходящим для интерполяции изображений является кубический B-сплайн (рис.5.10), поскольку в результате его применения получается функция, непрерывная и гладкая в узлах интерполяции. Ядро кубической свертки составляется из кусков кубических полиномов, определенных на подинтервалах  (-2,-1), (-1,0), (0,1), (1,2) по каждой из координат. Вне интервала (-2,2) интерполяционное ядро равно нулю. Двумерный кубический B-сплайн может быть записан как произведение двух одномерных интерполяционных функций по каждой из координат

 где  , так что

                                                         (5.22)

и , то есть ядро симметричное.

Как показали непосредственные исследования, кубический B-сплайн имеет тенденцию к сглаживанию передискретизованного изображения по сравнению с его первоначальной копией. Поэтому были предприняты определенные усилия для выбора кубического сплайна, более подходящего задачам обработки изображений. Общий кубический сплайн задается в виде

                             .                         (5.23)



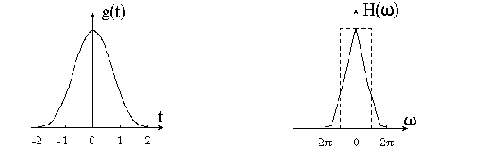
Рис.5.10. Кубический B-сплайн и модуль его Фурье-образа.

Имеется несколько естественных ограничений на данное интерполяционное ядро. Так, требуется чтобы значение интерполирующей функции в нуле было равно 1, а в точках с координатами 1 и 2 равно 0. Кроме того, необходимо, чтобы ядро было непрерывным в точках 0 и 1, чтобы наклон в точках 0 и 2 был равен 0, и первая производная была непрерывной. В совокупности это дает семь ограничений, в то время как неизвестных параметров восемь и, следовательно, нужно еще одно условие для однозначного определения интерполяционного ядра. В частности, если интерполяционную функцию привести в соответствие с первыми тремя членами ее разложения в ряд Тейлора, тогда неизвестный параметр должен быть равен (). Для практических задач удобнее все семь коэффициентов определить через неизвестный параметр   и интерполяционное ядро представлять в виде [5.10]:

           .                       (5.24)



Когда константа отрицательная, ядро (5.24) положительное в интервале от 0 до 1 и отрицательное в интервале от 1 до 2. Когда  возрастает, глубина боковых лепестков в интервале от 1 до 2 также увеличивается. Таким образом, с отрицательным значением свободной константы  интерполяционное ядро имеет вид усеченной sinc-функции. Выяснилось[5.11], что эта функция имеет более предпочтительные высокочастотные свойства, нежели кубический B-сплайн, и было предложено называть данную функцию высокоразрешающим интерполяционным кубическим сплайном.   Варьируя  значением  параметра

в пределах от -1 (рис.5.11.а) до -1/2 (рис.5.11.б), в каждом конкретном случае можно добиться приемлемой точности при передискретизации.



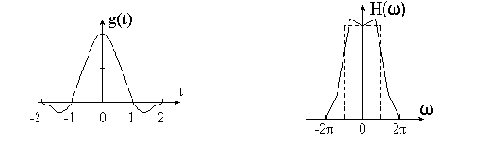
а)



б)

Рис.5.11. Высокоразрешающий интерполяционный кубический сплайн  и его частотная характеристика :

a) - a=-1; б) - а= - 0.5

5.3. Привязка изображений

В практике обработки изображений  задача поиска соответствия получила большое распространение и известна как проблема «поиска по образцу». Формально ее  можно рассматривать как процесс отождествления  эталонного изображения (образа фрагмента) на первом снимке с одним из множества образов фрагментов, лежащих в некоторой (задаваемой) области (зоне поиска) второго снимка . Алгоритмы установления сходства в своих основополагающих вариантах в той или иной степени связаны с получением характеристик стохастической взаимосвязи сравниваемых фрагментов изображений [5.2, гл.19].  Все они основываются на идеях корреляционной и спектральной теории сигналов, и для соответствующих критериев  получены экспериментальные характеристики основных процедур поиска по образцу.

5.3.1. Корреляционный критерий сходства

Будем считать, что изображение эталонного фрагмента (выбранного на снимке A и представляемого матрицей размером ), сравнивается с изображениями фрагментов снимка B в «зоне поиска»  размером . Перекрытие между фрагментами определяется шагом дискретной решетки  (в плоскости ), на которой заданы наблюдаемые переменные на A или  на B.


В процессе скользящего поиска ( когда каждый очередной фрагмент получается из предыдущего простым сдвигом на один дискрет) вычисляется «функция сходства» между изображением эталонного фрагмента  и изображениями текущих (контролируемых) фрагментов . Здесь требуется найти функцию сходства, которая бы с максимально возможной точностью и достоверностью позволяла локализовать фрагмент, соответствующий изображению эталонного фрагмента, фиксируя таким образом сопряженные точки на снимках.

Взаимно соответствующие элементы изображений одного объекта на снимках должны, очевидно, удовлетворять соотношению

                                (5.25)

где и - параметры контраста и средней освещенности; k, l - параметры относительного сдвига образца и его аналога на контролируемом снимке; - шум;



В такой формулировке процедура селекции образца должна найти параметры k и l, характеризующие сдвиг реперных фрагментов.

          Ради простоты будем считать, что параметр  не меняется по полю снимков, что позволяет перейти к центрированным переменным



                                    .

В качестве меры различия в точке  будем брать среднеквадратичную ошибку

                                          (5.26)

которая минимизируется перебором всех допускаемых сдвигов эталона по заданной области контролируемого снимка. Считается, что в точке экстремума реализуется сходство, если , где  - некоторый установленный порог. Из требования минимума ошибки находим оценку , подставляем ее в формулу (5.26) и приходим к выражению

            .                       (5.27)

Первый член выражения (5.27) - «энергия» эталонного сигнала, является величиной постоянной, не зависящей от параметров сдвига . Поэтому точка экстремума не изменится, если мы нормируем среднеквадратичную ошибку к энергии эталона 

    ,

и вместо минимума нормированной среднеквадратичной ошибки будем искать максимум коэффициента корреляции текущего фрагмента с эталоном



                .                              (5.28)

Соблюдение условий достоверности обнаружения также приводит к необходимости установления порога для величины взаимной корреляции : если , то с заданной вероятностью гарантируется действительное сходство найденной пары фрагментов. Величина порога определяется функцией распределения коэффициента корреляции (при случайных выборках) и задаваемой доверительной вероятностью принятия решения о действительном сходстве фрагментов.

Функционирование данного (по существу классического) алгоритма при наличии искажений в изображениях рассмотрено в работе [5.9]. Различия между эталонным и текущим () изображениями были обусловлены аддитивным шумом и геометрическими искажениями, которые моделировались аффинными преобразованиями координат изображений: , где ; - матрица относительного поворота изображений на угол ;  - коэффициент изменения масштаба. В работе показано, что среднее значение основного пика корреляционной функции геометрически искаженных изображений, нормированное к средней величине пика при отсутствии искажений, зависит от интенсивности искажений и при малых  и  имеет вид



Было практически продемонстрировано, что серьезным недостатком корреляционной меры сходства  является ее чувствительность к геометрическим искажениям видимых размеров сопряженных фрагментов  при изменении ракурса съемки.

 Обычно в качестве критериев эффективности процедур идентификации сходства принимается точность совмещения фрагментов и вероятность ложной привязки, когда экстремум функционала сходства значимо смещен относительно истинного положения. Анализ результатов имитационных экспериментов позволил сделать следующие выводы .

1. При наличии геометрических искажений существует оптимальный размер фрагмента эталонного изображения, позволяющий минимизировать вероятность ложной привязки. Оптимальный размер фрагмента пропорционален эффективному радиусу корреляции (полуширине графика автокорреляционной функции) и уменьшается с увеличением геометрических искажений.



2. При заданном уровне искажений размер эталонного изображения, при котором погрешность совмещения минимальна, меньше, чем размер изображения, необходимый для минимизации вероятности ложной привязки.

Здесь  можно порекомендовать использовать полезную модификацию метода идентификации сходства, заключающуюся в том, что искажения  геометрии на втором снимке (относительно первого) предварительно компенсируются аффинной (или полиномиальной) "подгонкой".  Например, параметры аффинного преобразования

=  ,   ,

можно оценивать адаптивно (в несколько "проходов"), когда на первом этапе задается достаточно большая зона  поиска по образцу, что позволяет на искаженном (по отношению к исходному) снимке находить сопряженные точки. Даже трех пар опорных точек достаточно, чтобы оценить  (в первом приближении) параметры аффинного преобразования и осуществить аффинную подгонку геометрии изображения  к геометрии изображения . Это дает возможность повторным просмотром найти уже существенно большее число пар сопряженных точек  на исходном и аффинно-преобразованном  снимках и  уточнить по ним  параметры  аффинной аппроксимации.  Дальнейшее повторение этой процедуры  позволяет, в принципе, идентифицировать любое (допустимое данной аппроксимацией) число пар сопряженных точек и, следовательно, добиться заданной точности в оценивании параметров геометрического преобразования.

          Поиск по образцу в данном методе сводится к вычислению нормированной взаимной корреляции распределения яркости (двумерного  сигнала) на текущем фрагменте первого снимка с распределениями яркостей  фрагментов, лежащих в некоторой предполагаемой окрестности образа этого фрагмента на аффинно-преобразованном втором снимке и определению целочисленных параметров взаимного смещения исходного фрагмента и его образа, устанавливаемого по экстремуму  корреляционного функционала.

5.3.2. Локальное уточнение сдвига

После определения целочисленных параметров смещения чаще всего требуется  локальное уточнение сдвига фрагментов в пределах дискрета (шага целочисленной решетки) [5.8, гл.15].


Чтобы найти соответствующий вектор сдвига  будем считать, что кросс-корреляционная функция  в окрестности точки экстремума  разлагается в ряд Тейлора:



(первые производные в точке экстремума равны нулю). Дифференцируя данное выражение, непосредственно получаем





В результате приходим к матричному уравнению для параметров :

  .                            (5.30)

Таким образом, в результате всех  вычислений, проведенных над элементами изображений пары снимков, координаты пар сопряженных точек , в целом связываются соотношением 

  .                    (5.31)

5.3.3. Кросс-спектральная мера сходства

Здесь мы разовьем далее охарактеризованный метод решения задачи привязки. Для этого  будем исходить из  исследования обобщенной кросс-спектральной меры сходства. Для единообразия запишем матрицу эталонного фрагмента в левом верхнем углу нулевой матрицы порядка  Это позволяет перейти от центрированных переменных  к спектральным компонентам (фурье-образам) изображений





Поскольку при смещении «образца» в области поиска  меняется только его фазовый спектр  то будем минимизировать функционал

(5.32)

по параметрам сдвига  где звездочкой обозначена операция комплексного сопряжения, а функция  осуществляет «взвешивание» разностной меры спектральных компонент. Так как «энергия» изображений фрагментов не зависит от параметров  то положение минимума функционала соответствует точке экстремума перекрестного члена при раскрытии скобок в (5.32)

                               (5.33)

Точность локализации определяется крутизной данной кросс-спектральной функции  вблизи экстремума, характеризующего положение образа эталонного фрагмента. С этой точки зрения наилучшей моделью для  служит дискретный вариант дельта функции  Нетрудно убедиться, что последнему условию удовлетворяет весовая функция  вида

                                                                                  (5.34)



так как в этом случае обратное дискретное фурье-преобразование



Полученный результат можно интерпретировать следующим образом. Обнаружитель с передаточной функцией (5.34) представляет собой «фазовый» фильтр, т.е. фильтр, который фазовую часть комплексного спектра изображений оставляет без изменений, а амплитудный спектр нормализует. Нетрудно  усмотреть, что в данном варианте кросс-спектральная мера есть фурье-образ функции когерентности



Тем самым можно отнести все признаки оптимальности когерентного функционала [5.6] и к кросс-спектральной мере сходства, допускающей к тому же эффективную реализацию на основе быстрого преобразования Фурье.



          a)                                                                  б)

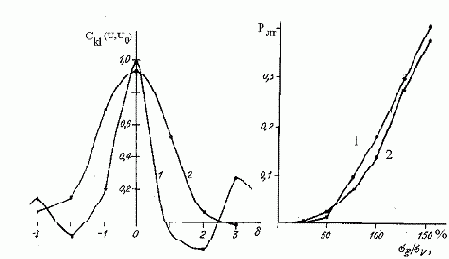
Рис.5.12. Меры эффективности алгоритмов идентификации сходства:

а - поведение кросс-спектральной меры сходства вблизи ее экстремума: 1 - отклик фазового фильтра, 2 - отклик корреляционного обнаружителя;

б - оценки вероятностей ложной привязки (ВЛП) в зависимости от отношения амплитуды шума  к амплитуде фонового сигнала (в %): 1 - ВЛП в фазовом алгоритме, 2 - в корреляционном алгоритме.

Следует отметить, что выражение (5.33) при соответствует классическому корреляционному алгоритму, реализуемому в спектральной области. Функционирование данного алгоритма при наличии геометрических искажений и выводы, сделанные на основе моделирования, выше были нами приведены.

Анализ результатов имитационных экспериментов показал [5.7], что аналогичные выводы справедливы и для когерентного (фазового) алгоритма. Однако рабочая зона идентификации фазового фильтра  (по величине допустимых геометрических искажений) меньше аналогичной зоны для корреляционного алгоритма. Это и понятно, так как чем меньше эффективный радиус кросскорреляционной функции сходства  , тем более чувствителен алгоритм к изменению геометрии идентифицируемых фрагментов. В частности, алгоритм нормированной корреляции ведет удовлетворительный поиск по образцу для снимков, развернутых на угол до  ( Алгоритм фазовой корреляции здесь нормально функционирует, если угол поворота не превышает  На рис.5.12.а представлено типичное поведение кросс-спектральной меры сходства в рассматриваемых вариантах, а на рис.5.12.б даны графики оцененных вероятностей ложной привязки в зависимости от уровня случайной составляющей сигнала на контролируемом снимке.


Видно, что фазовый фильтр в достаточно широком диапазоне мощностей помехи (до 55%) имеет меньшую вероятность ложной привязки фрагментов, нежели классический корреляционный алгоритм. Для иллюстрации изложенных методов здесь представлен результат привязки радиолокационных снимков.

 

Рис.5.13.Радиолокационные изображения местности, снятые при двух пролетах самолета (разные ракурсы съемки)

5.3.4. Привязка по локальным неоднородностям

 Если в некоторой части изображения уровень яркости более или менее постоянен или на одном из снимков искажен инородными включениями, то сопряженные точки искать достаточно трудно. Кросс-корреляционные методы, использующие фрагменты меньшие, чем данная область однородной яркости, не дадут ярко выраженного максимума, либо максимум не превысит заданный пороговый уровень.

 

Рис.5.14. Результаты привязки изображений

На левом снимке  рис. 5.14 большие светлые рамки соответствуют зонам поиска для правого снимка рис.5.13, малые рамки характеризуют размер эталонных фрагментов, выбираемых на левом снимке рис.5.13 (по изображениям соответствующих фрагментов вычислялась кросс-спектральная мера сходства). Смещение малых рамок от центра больших рамок указывает на величину найденных локальных геометрических деформаций между снимками. Правый снимок соответствует правому снимку на рис.5.13, геометрически преобразованному в формат левого снимка (полиномиальное преобразование третьей степени с параметрами, оценки которых мало отличаются от аффинного преобразования; передискретизация осуществлялась на основе высокоразрешающей бикубической сплайн-интерполяции) .Это достаточно хорошо видно на рис.5.14, где рамками обозначены фрагменты, для которых взаимная мера сходства между изображениями находится в доверительном интервале. В то же время в большей части областей снимков  критерий сходства не регистрировал действительного сходства в выбранных фрагментах зоны поиска. Поэтому может оказаться более разумным осуществлять поиск реперных фрагментов только в информационно - насыщенных областях, где яркость быстро меняется, например, на краях  между более или менее однородными областями.


Выделение краев [5.2, гл.17] можно рассматривать как средство быстрого предварительного просмотра эталонного изображения и отбора информативных областей. В полученных областях   далее выбираются эталонные реперные фрагменты и осуществляется поиск корреляционными методами соответствующих им фрагментов на контролируемых изображениях. В этом случае  привязка будет осуществляться по заведомо информативным областям, что повышает точность локализации сопряженных точек и уменьшает вероятность ложного отождествления.

ВОПРОСЫ К ГЛАВЕ 5

 

5.1. Охарактеризуйте круг проблем, решение которых приводит к привязке последовательности изображений и их взаимной геометрической коррекции.

5.2. Выстройте иерархию геометрических преобразований. Какие из них сохраняют параллельность прямых? 

5.3. Постройте матрицу поворота (в однородных координатах) вокруг точки плоскости  на угол  (указание: совместить центр поворота с началом координат, повернуть, вернуть центр поворота в прежнее положение и перемножить полученные матрицы элементарных преобразований). 

5.4. Чем отличается аффинная плоскость от евклидовой плоскости и от проективной плоскости?

5.5. В каких ситуациях рекомендуется применять полиномиальную аппроксимацию (в том числе и полиномы Чебышева) для описания геометрических деформаций?

5.6. Опишите  процедуру восстановления изображения в преобразованных координатах. Какие используются методы интерполяции и в чем их различие?

5.7. Назовите меры сходства изображений и охарактеризуйте их относительные свойства (смысл их оптимальности, точность локализации, достоверность, устойчивость к геометрическим деформациям).

5.8.  Опишите процедуру привязки изображений и методы ее ускорения. 


Содержание раздела

---

---