Фотограмметрия и стереовидение

Среди них - школы в области цифровой обработки изображений Самарского государственного аэрокосмического университета под руководством В.А. Сойфера и В.В. Сергеева и Ульяновского технического университета под руководством К.К. Васильева. Авторы выражают им свою признательность за то сотрудничество, к числу результатов которого относится и данное учебное пособие.

В обычном изображении трехмерного пространства информация о расстоянии до различных элементов сцены проявляется только в виде косвенных признаков: через относительные размеры объектов, затенение одних объектов другими, различной освещенностью и т.д. Один из способов получения информации о глубине состоит в регистрации нескольких изображений сцены под различными ракурсами. В этом случае точки сцены дают изображения, относительное положение которых зависит от расстояния до точки наблюдения. Оказывается, сопоставляя эти изображения, в ряде случаев можно реконструировать трехмерную структуру сцены. Основы теории определения  положения объектов в пространстве по их перспективным изображениям были положены еще в средние века, а в XVIII веке перспективные рисунки стали использоваться в топографических целях. Появление фотографии положило начало фотограмметрии – науке об определении формы, размеров и пространственного положения различных объектов посредством измерения их фотографических изображений. В начале XX века был изобретен стереокомпаратор – прибор для измерения пространственного положения объектов по паре перекрывающихся фотографических изображений. Интерес к методам восстановления трехмерной структуры сцен по их плоским изображениям возобновился в середине XX столетия в связи с исследованиями в области искусственного интеллекта, а практическая потребность в робототехнических устройствах, способных ориентироваться в трехмерном пространстве, постоянно поддерживает этот интерес в последние десятилетия.

В этой главе мы рассмотрим процесс формирования изображений, соотношения между координатами точек сцены и их изображениями и методы оценивания параметров системы регистрации и трехмерной структуры сцены.
6.1. Модель регистрирующей камеры

Строго говоря, различные точки пространства предметов отображаются оптической системой камеры в пространстве изображений на различных расстояниях от фокальной плоскости. Однако, если расстояние между камерой и наблюдаемой сценой значительно превышает фокусное расстояние оптической системы, можно считать, что изображение строится в ее фокальной плоскости. В этом случае можно воспользоваться проективной моделью камеры, в которой изображение трехмерного объекта  получается проектированием его в фокальную плоскость (плоскость изображения) через единственную точку, называемую оптическим центром. Прямая линия, перпендикулярная плоскости изображения и проходящая через эту точку, называется оптической осью камеры, а точка пересечения оптической оси с плоскостью изображения – главной точкой.

Определим в трехмерном пространстве ортогональную правую систему координат OXYZ, начало которой совпадает с оптическим центром, ось OZ - с оптической осью камеры. Такая система называется стандартной системой координат камеры. Пусть плоскость изображения находится на расстоянии  от оптического центра. В этой плоскости зададим систему координат oxy с началом в главной точке и осями ox и oy, параллельными осям OX и OY соответственно (рис. 6.1). Легко убедиться, что в стандартной системе координат проекцией точки трехмерного пространства  с координатами  является точка  в плоскости изображения с координатами , причем

, .                                            



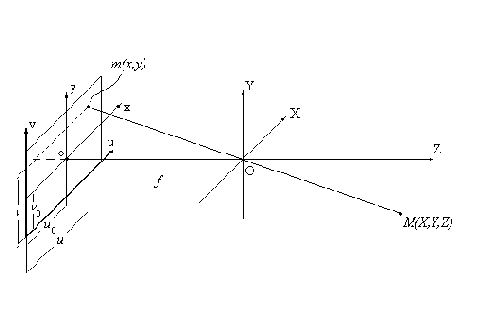
Рис.6.1. Система координат проективной камеры

Для полного описания камеры следует учесть, что для регистрации изображения в плоскости изображения камеры помещается какой-либо фотоприемник. В фотокамере это фотопластинка или фотопленка, в видеокамеру это видикон или фотоприемная полупроводниковая матрица, в некоторых специальных камерах – электромеханический сканер. В общем случае измерение координат в фотоприемнике осуществляется в  единицах, отличных от единиц, задающих координаты в стандартной системе.




Например, если используется матричный фотоприемник, его естественными координатами являются номер строки и номер столбца фотоприемной ячейки. Поэтому для полного описания камеры необходимо выразить координаты точки   в естественных единицах фотоприемника. В достаточно общем для любых фотоприемников виде (рис. 6.1) это может выглядеть как

 ,  ,

где  - координаты главной точки относительно начала координат фотоприемника (в естественных координатах фотоприемника);

  и   - масштабы вдоль осей ox  и oy (например, расстояния между ячейками матричного фотоприемника вдоль строк и столбцов).

В новой системе координаты проекции точки примут вид

                                   ,   .                                                      (6.1)

Для последующего изложения введем трехмерный вектор , соответствующий точке , и двумерный вектор , соответствующий точке . Определим также вектор однородных (см. гл. 5) внутренних координат камеры . Используя эти обозначения, соотношения (6.1) можно представить в компактной векторно-матричной записи:

,                                                         (6.2)

где - матрица, известная под названием матрицы внутренних параметров камеры, поскольку она содержит только параметры оптической системы и фотоприемника камеры.

6.2. Связь между различными системами координат

В общем случае трехмерные координаты точки могут быть заданы в системе, не совпадающей со стандартной системой координат камеры (назовем ее глобальной). Пусть OXYZ – глобальная система координат, а  - стандартная система координат камеры. Переход от системы OXYZ к системе   можно осуществить поворотом координатных осей к системе  и последующим смещением начала координат. Тогда связь между координатами точки в глобальной и стандартной системе может быть представлена как

                                                      ,                                                       (6.3)

где  и  - векторы пространственных координат точки  в глобальной и стандартной системах, соответственно; - матрица размерности , описывающая поворот стандартной системы координат относительно глобальной; компонентами матрицы являются направляющие косинусы осей глобальной системы в стандартной системе координат ;  - трехмерный вектор смещения начала координат глобальной системы  относительно начала координат стандартной.





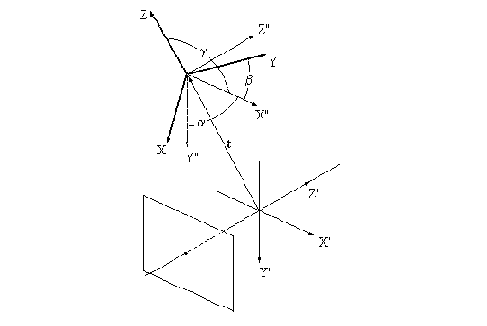
Рис.6.2. Переход от глобальной системы координат к стандартной системе координат камеры.

На рис. 6.2. схематически показано преобразование координат. Здесь - углы, образованные осью  с осями ,  и  соответственно. Элементы первой строки матрицы   [6.1, п.14.10] содержат  косинусы этих углов: ,  ,  . Аналогично, вторая и третья строки матрицы содержат косинусы углов, образованных соответственно осями  и  с осями глобальной системы координат.

Особенность матрицы  состоит в том, что она зависит только от трех параметров, поскольку  все девять ее элементов связаны  шестью уравнениями связи и, следовательно, не являются независимыми.  Обозначив строки матрицы в виде векторов ,  и , эти уравнения можно представить в виде:

                  ,  ,  ,  , ,  ,                         (6.4)

Уравнения (6.4) являются условиями взаимной ортогональности векторов . Матрица, построенная из таких векторов, называется ортогональной. Для ортогональной матрицы справедливо соотношение . Условие взаимной ортогональности векторов  в трехмерном пространстве можно выразить в другой удобной форме, которая понадобится нам позже:

                           , , .                           (6.5)

Верхний знак соответствует случаю, когда матрица  представляет преобразование, не изменяющее взаимной ориентации осей системы, а нижний – преобразование, изменяющее правую систему координат на левую и наоборот.

 Смысл вектора  ясен непосредственно из рисунка.

6.3. Стереоскопическая система

Рассмотрим ситуацию, когда две камеры, находящиеся в разных точках,  регистрируют одну и ту же  сцену. Пара изображений, получаемых при этом, называется стереопарой. Обратимся сначала к простейшему случаю. Пусть одинаковые камеры расположены так, что их оптические оси параллельны, а прямая, проходящая через оптические центры, перпендикулярна оптическим осям (эта прямая называется базовой линией, а ее отрезок, заключенный между оптическими центрами – базой).  Положим длину базы равной .


Выберем такую глобальную систему координат, начало которой   расположено на базовой линии посередине между оптическими центрами камер, ось  параллельна оптическим осям, а ось  направлена вдоль базовой линии (рис. 6.3). Пусть начала координат в плоскостях изображений камер совпадают с главными точками (), а единицы измерения координат в глобальной системе и в плоскостях изображения камер одинаковы ().

Выберем точку  с глобальными координатами . Координаты ее проекции в плоскости изображения первой (левой) камеры обозначим через , а в плоскости изображения второй (правой) камеры – через . (Проекции одной и той же точки  в плоскостях изображений разных камер называются сопряженными точками.) Нетрудно проверить, что

,  , .

Заметим, что в направлении, перпендикулярном направлению базовой линии, координаты сопряженных точек (-координаты) совпадают. Это обстоятельство имеет большое значение при автоматизированном поиске сопряженных точек на стереопаре, позволяя существенно сократить размеры зоны поиска. Из первых двух соотношений следует, что

.                                                (6.6)



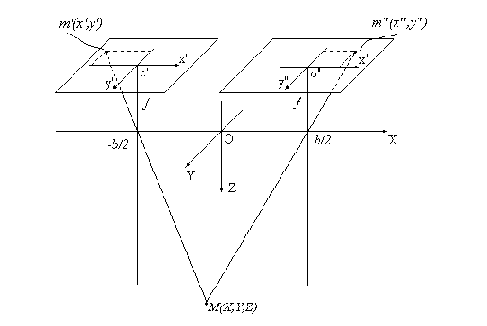
Рис.6.3. Простейшая стереоскопическая система

Это означает, что, зная геометрию съемки и выполнив измерения координат проекций одной и той же точки в плоскостях изображения камер, можно вычислить глубину (координату ) этой точки. Более того, полученные соотношения позволяют вычислить полностью трехмерные координаты точки:

, .                                         (6.7)

Разность  называется диспарантностью.  Из (6.6) и (6.7)  следует, что ошибки в координатах проекций сильнее сказываются при малой диспарантности и, следовательно, расстояния до далеких объектов измеряются менее точно, чем до близких. С другой стороны, при фиксированной дальности диспарантность пропорциональна размеру базы, следовательно, точность измерений повышается с увеличением базы. Далее мы, однако, увидим, что увеличение базы может привести к ошибкам, которые не компенсируются увеличением точности измерений.



Теперь рассмотрим общий случай, когда оптические оси камер не параллельны, и направление смещения оптического центра одной камеры относительно оптического центра другой произвольно (рис.6.4). Введем для каждой камеры свою стандартную систему координат, так как это было сделано в разделе 6.1. Пусть  первой камере соответствует система координат , а второй –  (рис. 6.4). Пусть вектор  характеризует координаты некоторой точки  трехмерного пространства в системе первой камеры, а вектор  - в системе второй. Переход от глобальной системы координат к стандартным системам первой и второй камер осуществляется с помощью преобразований  и  соответственно. Учитывая это, легко показать, что связь между векторами  и  задается соотношением

,                                              (6.8)

где - ортогональная матрица, описывающая ориентацию системы координат второй камеры относительно первой, а - вектор трансляции, определяющий положение оптического центра второй камеры в системе координат первой. Матрицу  и вектор  принято называть внешними параметрами системы регистрации.



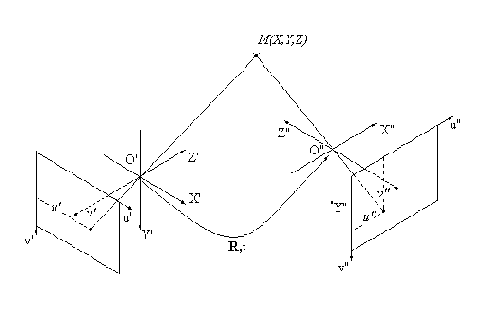
Рис.6.4. Система двух произвольно ориентированных камер

Используя (6.2) из (6.8) можно получить соотношение, связывающее координаты сопряженных точек (в координатах фотоприемника) :

,                                               (6.9)

где(см. (6.2))               ,  .                                (6.10)

(Предполагается, что регистрация может выполняться двумя различными камерами, внутренние параметры которых определяются матрицами  и ).

Уравнения (6.8) и (6.2) позволяют оценить трехмерные координаты точки  в системе координат любой из камер, если известны внешние параметры системы камер и удается измерить координаты изображений этой точки в плоскостях изображения камер (т.е. оценить векторы  и ). Поскольку компоненты векторов  и  могут содержать ошибки, реально соотношение (6.9) принимает вид:

,

где - вектор невязки, обусловленный наличием ошибок измерений.



Учитывая это, для оценивания неизвестных  и  можно воспользоваться методом наименьших квадратов (МНК), суть которого состоит в том, чтобы найти такие оценки  и , которые бы минимизировали сумму квадратов компонент (норму) вектора невязки: . Приравнивая частные производные  по  и  нулю (условие достижения экстремума) получим систему, состоящую из двух скалярных уравнений

,

разрешая которую относительно  и  получим

.            (6.11)

Теперь, используя (6.2), можно вычислить вектор трехмерных координат точки  в системе любой из камер:

,    .                                (6.12)

Из всего изложенного выше следует, что для оценивания трехмерных координат некоторой точки по стереопаре необходимо: а) знать внутренние параметры камер (задача калибровки), б) знать параметры взаимного расположения камер (задача взаимного ориентирования), в) найти и  определить на изображениях координаты соответствующих данной точке сопряженных точек (задача поиска сопряженных точек). 

6.4. Калибровка камеры

Заметим сразу, что поскольку фокусное расстояние  и масштабные коэффициенты  и  входят в матрицу  только в комбинациях  и , то раздельно оценить все три этих параметра невозможно. Введем новые параметры  и  , которые и будут подлежать оцениванию.

Пусть камера регистрирует сцену, содержащую  опорных точек, и трехмерные координаты точек известны в глобальной системе координат. Задача состоит в том, чтобы по трехмерным координатам опорных точек  и координатам их проекций в плоскости изображений камеры ,   оценить элементы матрицы .

Если положение камеры относительно этой системы известно (т.е. известны матрица  и вектор  в выражении (6.3)), можно сразу пересчитать координаты опорных точек в стандартную систему камеры и для оценивания внутренних параметров воспользоваться соотношениями (6.1), подставив вместо   и   и   соответственно. Перепишем (6.1) в виде

, .            

Для  опорных точек получим две системы, состоящие из   линейных уравнений каждая, относительно неизвестных ,  и , :



      ,     

,                                                   (6.13)

где ,  ,   ,

, ,  .

Очевидно, достаточно двух опорных точек, чтобы получить оценки внутренних параметров камеры:

,        ,

,   .

Обратим внимание на необходимость выполнения условий  и , которые формально выражают требование, чтобы в плоскости изображения камеры проекции опорных точек не лежали на прямых, параллельных осям координат.

          Для увеличения точности оценок внутренних параметров следует использовать большее количество опорных точек. Системы (6.13) в этом случае становятся переопределенными, и для их решения можно применить МНК. Минимизируя норму вектора невязки  получим оценки внутренних параметров

,       .

Рассмотрим теперь задачу калибровки в более общей постановке. Пусть неизвестны не только матрица , но и положение камеры относительно глобальной системы координат (т.е. матрица  и вектор  в выражении (6.3)). Такая постановка обусловлена тем, что технически довольно сложно выполнить точные измерения положения камеры и особенно ее ориентации относительно произвольной системы координат. Используя (6.2) и (6.3) и вводя вектор , связь между глобальными координатами опорной точки  и координатами ее изображения можно представить в виде

.                       (6.14)

Матрица  имеет размер  и называется калибровочной. Обозначим

,  ,

,  ,                      (6.15)

,                  .

Отметим два важных свойства этой матрицы, которые легко получить из (6.15), учитывая (6.4)  и (6.5):

 ,

.                                      (6.16)

Оказывается, что если элементы калибровочной матрицы  известны, через них можно вычислить матрицы ,  и  вектор . Действительно, учитывая (6.4), легко показать, что

,

,

,                                                     (6.17)

.         

Кроме того, непосредственно из (6.14) следует, что

,

,

,

,                                          (6.18)



,

.

Задача калибровки, следовательно, сводится к предварительному оцениванию элементов матрицы .

Рассмотрим сначала линейный метод оценивания матрицы . Запишем матричное уравнение (6.14) как систему трех обычных уравнений

,

,

,

или, подставляя в два первых уравнения значение  из третьего,

,       

.

Зная координаты   опорных точек в трехмерном пространстве и координаты их проекций  в плоскости изображения камеры, получим однородную систему из  линейных уравнений относительно 12 неизвестных элементов калибровочной матрицы :

.   (6.19)

Представим эту систему в матрично-векторном виде:

,                                              (6.20)

где



,  .

Сначала рассмотрим некоторые общие особенности этой системы. Очевидно, что одним из решений этой системы является тривиальное , которое не имеет физического смысла. Известно [6.2, с.153], что если однородная линейная система имеет хотя бы  одно ненулевое решение, то она имеет бесконечное множество решений, причем, если  - решение, то и  , где - произвольное число, тоже является решением. Здесь необходимо различать два случая.

Первый – когда ранг матрицы  на единицу меньше размера вектора . Тогда существует только одно (с точностью до произвольного скалярного множителя) решение. Именно этот случай и представляет практический интерес. Для реализации этого условия необходимо (но недостаточно), чтобы количество уравнений в (6.20) было не менее 11, следовательно, количество опорных точек  должно быть не менее шести. Ограничить множество решений можно, воспользовавшись первым из условий (6.16). Действительно, определив некоторое решение , в качестве оценки компонент калибровочной матрицы выберем  такое, чтобы  Такая нормировка определяет калибровочную матрицу с точностью до знака. Выбрать правильный знак матрицы можно, например, зная, с какой стороны от плоскости  глобальной системы координат находится камера, и учитывая первое из соотношений (6.18).


Знак   должен совпадать со знаком компоненты  вектора трансляции.

Второй случай реализуется, если ранг  меньше размера вектора  на два и более. Здесь может существовать множество различных решений системы, среди которых осуществить правильный выбор без привлечения дополнительных данных невозможно. Показано [6.3], что такая ситуация возникает, в частности, если все опорные точки лежат в одной плоскости. Чтобы избежать этой ситуации, в качестве тестового объекта часто используют объект, приведенный на рис. 6.5.



Рис.6.5. Калибровочный объект

Рассмотрим теперь непосредственно метод решения системы (6.20). Обычно, чтобы уменьшить влияние ошибок измерений трехмерных координат опорных точек и координат их изображений в камере, используют  больше, чем шесть опорных точек. Тогда система (6.20) становится переопределенной. Кроме того, как и в разделе 6.2, из-за ошибок в измерениях координат реально система (6.20) принимает вид

,                                    

где , как и в п.6.2, - неизвестный вектор невязки, обусловленный наличием ошибок измерений.

          В этой ситуации можно снова воспользоваться МНК, согласно которому в качестве оценки вектора  следует принять такой, который минимизирует значение функционала  при условии  (см.(6.16)). Поскольку функционал  представляет собой квадратичную форму с неотрицательно определенной симметричной матрицей , то  минимума по  при условии   он достигает, если  - собственный вектор матрицы , соответствующий ее минимальному собственному числу [6.4, с.64]. Заметим, что  .  (Собственным вектором матрицы  называется вектор , который удовлетворяет уравнению , где - скалярный множитель, называемый собственным числом матрицы  ).

          Другой подход к оцениванию матрицы  основан на минимизации расстояний между измеренными проекциями опорных точек и вычисленными в соответствии с (6.14). Определим величину

,

которая представляет сумму квадратов этих расстояний, и минимизируем ее по  с учетом ограничений (6.16).


Решить эту задачу можно посредством методов условной минимизации [6.5, гл.VI], изложение которых выходит за рамки данного учебника. Следует отметить только, что такой подход обычно дает результаты оценивания, более устойчивые к ошибкам измерений, чем рассмотренный выше линейный.

6.5. Взаимное ориентирование

В предыдущем параграфе показано, как с помощью тестовой сцены не только оценить внутренние параметры камеры, но и определить ее положение относительно системы координат, в которой задана тестовая сцена. Последнее позволяет нам, откалибровав две камеры по одной тестовой сцене, определить их взаимное положение (см. (6.8)). Однако если внутренние параметры камер определены их конструкцией и могут считаться постоянными, то взаимное положение камер во многих практических случаях может изменяться в процессе регистрации сцены. В связи с этим возникает задача взаимного ориентирования, не предполагающая наличия тестовой сцены.

Рассмотрим снова пару камер, внутренние параметры которых известны, но неизвестны внешние параметры (матрица  и вектор ). Умножив обе части выражения (6.8) слева сначала векторно на , а затем скалярно на , получим

.

Это соотношение формально выражает тот факт, что векторы ,  и  лежат в одной плоскости, проходящей через три точки: оптические центры камер  и  и точку наблюдения .  Выражая  через  из (6.10) получим:

                                     (6.21)

или, учитывая свойства смешанного произведения векторов,

.                                  (6.22)

Эквивалентные соотношения (6.21) и (6.22) являются основой для  оценивания матрицы  и вектора . Предположим, что известны координаты  пар сопряженных точек и, соответственно,  пар векторов  и   .

Рассмотрим метод оценивания  и , использующий (6.22). Так как это соотношение справедливо для любой пары сопряженных точек, мы имеем систему из  уравнений относительно неизвестных  и , которую можно представить в виде:

,   где  .                     (6.23)



Система (6.23) является однородной линейной по . Это означает, что вектор трасляции можно  оценить  только с точностью до постоянного множителя. Вводя условие нормировки , количество возможных решений можно ограничить двумя, отличающимися знаком. Вопрос о выборе знака будет рассмотрен позже. Система (6.23) содержит пять неизвестных, так как матрица  в силу условий нормировки и ортогональности зависит от трех параметров, а вектор  с учетом введенной нормировки – от двух. Поэтому число уравнений в системе, следовательно и число пар известных сопряженных точек  должно быть не менее пяти.

Поскольку на практике в матрицу  входят не точные значения координат сопряженных точек, а результаты их измерений, которые могут содержать ошибки,  реально система (6.23) имеет ненулевую правую часть, т.е.

,

где , как и в п.6.2, - вектор невязки, обусловленный наличием ошибок измерений.

Согласно МНК в качестве оценок матрицы вращения и вектора трансляции следует выбрать такие  и , которые минимизируют значения функционала . Как упоминалось ранее, при условии  квадратичная форма  достигает минимума по  (- минимальное собственное число матрицы ), если  - собственный вектор матрицы, соответствующий . Поэтому процедуру оценивания  и  можно разбить на два этапа. На первом находится матрица , минимизирующая . На втором оценивается собственный вектор матрицы , соответствующий . Существует множество алгоритмов и их программных реализаций для вычисления собственных векторов, поэтому второй этап не вызывает трудностей.

Значительно более сложной задачей является задача оценивания матрицы . Один из возможных алгоритмов состоит в следующем [6.6]. Известно [6.1, п.14.10], что матрица  может быть представлена в виде , где

 ,   ,

.

Углы ,  и   и есть те три неизвестных параметра, от которых зависит матрица . На практике всегда известен диапазон, в котором они  могут лежать. Выполняя в этом диапазоне полный перебор по всем углам с достаточно грубым шагом (например, 1°) можно приблизиться к значениям, удовлетворяющим требованиям минимизации функционала  по .


Затем в окрестности этих значений для уточнения положения минимума можно воспользоваться одним  из известных методов минимизации [6.5, гл.V] (например, наискорейшего спуска, Ньютона, Маркуардта).

Наконец, получив оценки  и , можно, используя (6.11), оценить и -координаты наблюдаемых точек. Из способа задания систем координат (см. рис.6.4)  следует, что  и  должны быть положительными. Этим условием и определяется выбор правильного знака вектора трансляции .

В заключение необходимо сказать, что развитием темы взаимного ориентирования является задача самокалибровки системы камер, целью которой является оценивание как внутренних так и внешних параметров. Не останавливаясь на этой задаче подробно, отметим только, что в системе, состоящей из двух, даже одинаковых, камер, данных для самокалибровки недостаточно. Добавление третьей камеры с теми же внутренними параметрами делает самокалибровку возможной. Подробное исследование этого вопроса можно найти в [6.7].

Отметим, что задача определения взаимного положения камер может иметь и другую трактовку. Предположим, что движущаяся камера непрерывно регистрирует некоторую сцену. Тогда, анализируя последовательность изображений и решая эту задачу, можно определить характер движения камеры в пространстве.

6.6. Поиск сопряженных точек

          Центральной проблемой компьютерного стереозрения является поиск сопряженных точек. Задача автоматизированного поиска сопряженных точек состоит в следующем: на одном из изображений выбрана точка , являющаяся проекцией некоторой точки  трехмерного пространства, необходимо на втором изображении найти точку  – проекцию той же точки. Достаточно очевидно, что фактически при решении этой задачи речь идет об отождествлении не отдельных точек, а фрагментов изображений, лежащих в окрестностях этих точек. Здесь возникает два вопроса. Первый – если на одном изображении указана точка, где на втором изображении искать сопряженную? Второй – что является критерием «похожести» фрагментов?

Оказывается, на первый вопрос можно дать достаточно строгий ответ.


Обратимся к соотношению (6.21). Известно [6.8, Приложение], что векторное произведение  можно представить как , где матрица  имеет вид:

.

Тогда (6.21) можно представить как

                                              (6.24)

или

                                                          ,

где

                                  .                                     (6.25)

С другой стороны, любая прямая линия на плоскости может быть задана уравнением  или, в векторном виде,  , где , . Сравнивая уравнение прямой с (6.24) и с (6.25) приходим к выводу, что (6.24) задает в плоскости изображения первой камеры прямую

                                                (6.26)

с вектором коэффициентов ,

а в плоскости изображения второй камеры - прямую

                                                (6.27)

с вектором коэффициентов .

          Это значит, что если в плоскости изображения первой камеры указана точка с вектором внутренних координат , то сопряженная точка в плоскости изображения второй камеры может лежать только на прямой, заданной уравнением (6.26). Аналогичное правило справедливо и для точек, заданных в плоскости изображения второй камеры.

Этот результат имеет наглядную геометрическую иллюстрацию (рис.6.6).



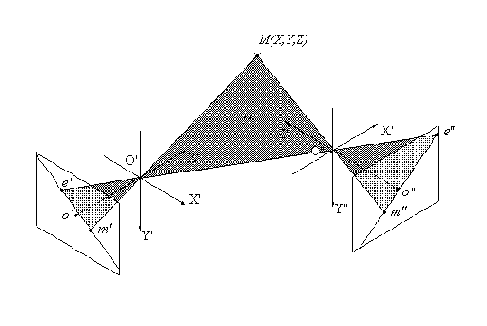
Рис. 6.6. Эпиполярные линии

Оптические центры камер  и   и наблюдаемая точка образуют плоскость , которая пересекает плоскости изображения камер по прямым  и , где точка  является изображением оптического центра  второй камеры в плоскости первой, а  - изображением центра  в плоскости второй. С другой стороны, если задана точка , то точка   трехмерного пространства может лежать только на прямой, проходящей через  и оптический центр . Следовательно, ее проекция в плоскости изображения второй камеры должна лежать в плоскости , лежащей на этой прямой и оптическом  центре  ,  а значит, на линии пересечения плоскости  и плоскости изображения второй камеры. Линии пересечения плоскости  с плоскостями  изображений камер называются эпиполярными линиями.



Практическая ценность полученного результата заключается в том, что его использование при поиске сопряженных точек позволяет существенно сократить размер зоны поиска, выполняя поиск не на всем изображении, а только вдоль эпиполярной линии, и тем самым снизить вероятность ложной идентификации фрагментов.

В отличие от рассмотренных ранее вопросов,  сопоставление окрестностей сопряженных точек не поддается строгой  формализации, поскольку в его  основе лежит проблема идентификации по изображениям фрагментов реального трехмерного мира, которые с трудом поддаются адекватному формальному  описанию. Возникающие при съемке и зависящие от ракурса проективные и яркостные искажения приводят к тому, что в изображениях одних и тех же участков сцены, снятых под разными ракурсами, могут появиться значительные отличия. Принципиально важно то, что эти отличия зависят не только от геометрии съемки, но и от геометрических и физических характеристик самой сцены. Расположение источника света по отношению к поверхности сцены влияет на распределение освещенности. Положение элементов сцены, их отражательные и рассеивающие свойства определяют количество энергии, попадающей в объективы камер, а следовательно, и локальные отличия в яркости сопряженных фрагментов изображений.

На рис.6.7 схематично показаны некоторые причины возникновения различий в изображениях.  Пунктиром показаны индикатрисы излучения (рассеяния) в точках  и  наблюдаемой поверхности.

Видно, что интенсивность излучения из точки   в направлении левой камеры (с оптическим центром ) больше, чем в направлении правой камеры (с оптическим центром ).  Точка , наоборот, излучает в камеру  слабее, чем в камеру .  Жирными столбиками показана интенсивность сигнала в изображениях этих точек в левой (и ) и правой (и ) камерах. Более того, точка  вообще не видна в левой камере, поскольку ее загораживает участок поверхности .

Величина различий зависит от разницы в ракурсах съемки. Как правило, чем больше эта разница (в частности, чем больше база), тем менее похожими становятся изображения.


Поэтому все методы отождествления окрестностей сопряженных точек в большей или меньшей степени опираются не на формальный подход, а на здравый смысл.



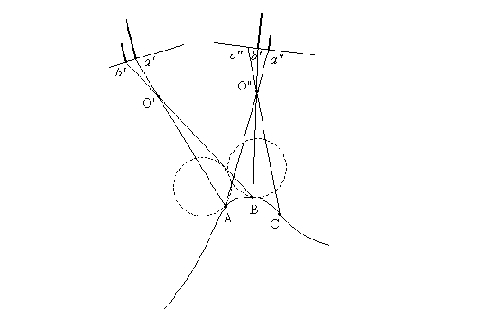
Рис.6.7. Проективные и яркостные искажения

Одним из наиболее распространенных методов идентификации является корреляционный. Детальное описание корреляционного метода приведено в гл.6. При незначительных отличиях в ракурсах съемки и на достаточно гладких поверхностях от него можно ожидать хороших результатов. На рис.6.8 (а и б)  приведена пара вертолетных снимков района озера Карымское (Камчатка), на которые нанесена прореженная сетка сопряженных точек, найденных корреляционным методом, а на рис.6.8.в показана поверхность, «натянутая» на трехмерные точки, координаты которых вычислены методом, изложенным в п.6.2. Следует заметить, что построение поверхности, лежащей на заданном множестве трехмерных точек, представляет собой самостоятельную нетривиальную задачу, рассмотрение которой выходит за рамки темы, обсуждаемой в этой главе.

На снимках есть области, где сопряженные точки не удалось найти. Причин этому несколько. Часть сцены, видимая в правой части правого снимка, просто не попала в поле зрения левой камеры. Кроме этого, на снимках есть участки с мало изменяющейся яркостью. На таких участках корреляционный критерий не дает хорошо выраженного максимума, поэтому здесь координаты сопряженных точек определяются с большими погрешностями. Более того, здесь велика вероятность ложных отождествлений. Пространственное представление о таких участках получить без привлечения дополнительной информации невозможно. Если размеры этих участков малы, а по косвенным признакам можно предположить, что поверхность сцены изменяется плавно, можно интерполировать трехмерную структуру участков с их границ внутрь, как это сделано для участков  и .

Если их размеры велики, или сопряженные точки на границах не определены, восстановить трехмерную структуру участка не удается (участки  и ).

Для того, чтобы восстановить мелкую структуру сцены, необходимо, чтобы сопряженные точки лежали достаточно часто.


В приведенном примере для построения рельефа  найдено более 7000 точек.

а)	б)
в)
Рис.6.8. Восстановление поверхности трехмерной сцены по стереопаре (приведено с любезного согласия авторов [6.9])

Сложность применения корреляционного метода заключается в том, чтобы подобрать такие размеры сопоставляемых фрагментов, при которых отличия в тождественных фрагментах еще невелики (для этого нужно уменьшать размеры), а оценка коэффициента корреляции остается достоверной (для этого размеры надо увеличивать). Но самым серьезным его недостатком является чувствительность к масштабным искажениям, присутствующим в отождествляемых фрагментах. Простейший способ  уменьшения масштабных различий в сопряженных фрагментах  состоит в использовании предварительной аффинной подстройки изображений. Этот способ, однако, оказывается недейственным при вариациях высот в сцене, сравнимых с расстоянием от сцены до системы камер, поскольку в этом случае появляются значительные локальные масштабные искажения.

Влияние яркостных искажений можно попытаться устранить, отказавшись от сопоставления фрагментов исходных изображений, и перейдя к сопоставлению фрагментов контурных изображений, где выделены края, т.е. переходы между областями с постоянной яркостью. На таких переходах, как известно,  градиент яркости имеет максимум, а лапласиан обращается в нуль. Это обстоятельство и используется для выделения краев [6.10, п.17.4]. Существенным моментом является то, что контуры на изображениях непрерывных поверхностей должны располагаться в одинаковом порядке, как это видно на рис. 6.9 (изображения точек ,  и ). Это ограничение позволяет в некоторой степени ослабить влияние масштабных искажений. Однако и здесь, как и в корреляционном методе, существует проблема ложного отождествления. Связана она, в частности, с тем, что видимая часть поверхности зависит от ракурса наблюдения (поэтому, например, на рис.6.9 изображение точки  в правой камере отсутствует), и на разных изображениях могут пропадать разные края.


Кроме того, сама задача выделения краев только на первый взгляд кажется такой простой. В действительности неизбежное присутствие шумов в изображениях может привести к частичному исчезновению контуров или появлению ложных. Идея поиска сопряженных точек с помощью отождествления краев была особенно популярна у биологов и психологов, исследовавших механизмы зрения [6.11], но, как нам кажется, в таком идеальном виде практического применения не нашла.

Еще один подход к поиску сопряженных точек опирается на предварительный раздельный анализ изображений, позволяющий выделить на них некоторые характерные объекты или особенности. Так на аэроснимках городских территорий можно попытаться выделить перекрестки, отдельные дома или их фрагменты, деревья и т.п., а затем  выполнить их отождествление между снимками.

По-видимому, наиболее удачных результатов можно ожидать от комбинированного использования всех этих методов и применения итеративной схемы, когда по найденным сопряженным точкам строится оценка поверхности, с учетом которой изображения подвергаются   масштабной коррекции и выполняется поиск новых сопряженных точек.



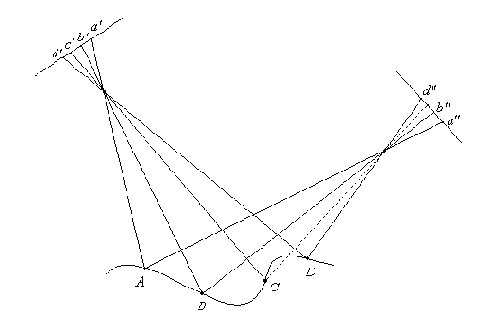
Рис.6.9. Упорядочение сопряженных точек в случае непрерывных поверхностей

 

ВОПРОСЫ К ГЛАВЕ 6

6.1. Какой смысл имеет знак при  в выражении (6.1)?

6.2. Какой вид примет выражение (6.3), если вектор трансляции будет задан в глобальной системе координат?

6.3. Обратимся к рис. 6.3. Какой вид будут иметь матрицы , ,  и вектор  в выражении (6.9) для ситуации, приведенной на рисунке?

6.4. Пусть в ситуации, изображенной на рис. 6.3, векторы   и  внутренних координат проекций точки  в плоскостях изображений левой и правой камер известны. Получите оценки трехмерных координат точки  в системах координат правой и левой камер, пользуясь выражениями (6.11) и (6.12). Сравните полученный результат с (6.6) и (6.7). Объясните отличия.

6.5. Почему в предыдущем вопросе векторы   и  имеют одинаковые - компоненты?

6.6. Докажите справедливость соотношений (6.17).


Содержание раздела

---

---