Фильтрация изображений

Обычно изображения, сформированные различными информационными системами, искажаются действием помех. Это затрудняет как их визуальный анализ человеком-оператором, так и автоматическую обработку в ЭВМ. При решении некоторых задач обработки изображений в роли помех могут выступать и те или иные компоненты самого изображения. Например, при анализе космического снимка земной поверхности может стоять задача определения границ между ее отдельными участками - лесом и полем, водой и сушей и т.п. С точки зрения этой задачи отдельные детали изображения внутри разделяемых областей являются помехой.

Ослабление действия помех достигается фильтрацией . При фильтрации яркость (сигнал) каждой точки исходного изображения, искаженного помехой, заменяется некоторым другим значением яркости, которое признается в наименьшей степени искаженным помехой. Что может послужить основой для таких решений ? Изображение часто представляет собой двумерную функцию пространственных координат, которая изменяется по этим координатам медленнее (иногда значительно медленнее), чем помеха, также являющаяся двумерной функцией. Это позволяет при оценке полезного сигнала в каждой точке кадра принять во внимание некоторое множество соседних точек, воспользовавшись определенной похожестью сигнала в этих точках. В других случаях, наоборот, признаком полезного сигнала являются резкие перепады яркости. Однако, как правило, частота этих перепадов относительно невелика, так что на значительных промежутках между ними сигнал либо постоянен, либо изменяется медленно. И в этом случае свойства сигнала проявляются при наблюдении его не только в локальной точке, но и при анализе ее окрестности. Заметим, что понятие окрестности является достаточно условным. Она может быть образована лишь ближайшими по кадру соседями, но могут быть окрестности, содержащие достаточно много и достаточно сильно удаленных точек кадра.

В этом последнем случае, конечно, степень влияния далеких и близких точек на решения, принимаемые фильтром в данной точке кадра, будет совершенно различной.

Таким образом, идеология фильтрации основывается на рациональном использовании данных как из рабочей точки, так и из ее окрестности. В этом проявляется существенное отличие фильтрации от рассмотренных выше поэлементных процедур: фильтрация не может быть поэлементной процедурой обработки изображений.

Задача заключается в том, чтобы найти такую рациональную вычислительную процедуру, которая позволяла бы достигать наилучших результатов. Общепринято при решении этой задачи опираться на использование вероятностных моделей изображения и помехи, а также на применение статистических критериев оптимальности. Причины этого понятны - это случайный характер как информационного сигнала, так и помехи и это стремление получить минимальное в среднем отличие результата обработки от идеального сигнала. Многообразие методов и алгоритмов связано с большим разнообразием сюжетов, которые приходится описывать различными математическими моделями. Кроме того, применяются различные критерии оптимальности, что также ведет к разнообразию методов фильтрации. Наконец, даже при совпадении моделей и критериев очень часто из-за математических трудностей не удается найти оптимальную процедуру. Сложность нахождения точных решений порождает различные варианты приближенных методов и процедур.

3.1. Оптимальная линейная фильтрация.

Уравнение Винера-Хопфа

Пусть

- значение яркости изображения - полезного сигнала на пересечении

-ой строки и

-го столбца, а наблюдаемое на входе фильтра изображение описывается моделью:

. (3.1)

Здесь

- значение помехи в точке с координатами

- функция, описывающая взаимодействие сигнала и помехи, а

- соответственно число строк и столбцов в кадре.

В дальнейшем будем придерживаться принятой при цифровой обработке изображений декартовой системы координат с началом в левом верхнем углу кадра и с положительными направлениями из этой точки вниз и вправо.

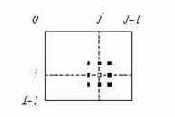
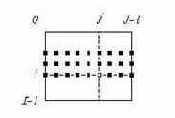
На рис. 3. 1 показаны примеры окрестностей различных типов, изображенные в виде совокупностей точек. Центром окрестностей, рабочей точкой, в которой осуществляется обработка, является точка с координатами

(на рис. 3.1 не зачернена). В зависимости от типа окрестности различают каузальную, некаузальную и полукаузальную фильтрацию изображений. Понятие


а)	б)	в)
Рис. 3.1 Примеры окрестностей различных видов

каузальности (причинно-следственной зависимости) связывают с соотношением координат текущей точки

и точек, входящих в окрестность. Если обе координаты (номер строки и номер столбца) всех точек окрестности не превышают соответствующих координат текущей точки, то окрестность и использующая ее обработка называются каузальными. Пример такой окрестности представлен на рис. 3.1.а.

Некоторые точки окрестности, приведенной на рис. 3.1.б, удовлетворяют принципу каузальности. Вместе с тем, здесь имеются и такие точки, обе координаты которых превышают соответствующие координаты рабочей точки. Фильтрация, опирающаяся на использование окрестностей с сочетанием таких свойств, называется некаузальной.

Окрестности, показанной на рис. 3.1.в, соответствует полукаузальная фильтрация. Одна из координат всех точек окрестности - в данном примере номер строки - не превышает соответствующей координаты рабочей точки. Вторая же координата - в примере номер столбца - у некоторых точек также не превышает соответствующей координаты рабочей точки. Однако среди точек окрестности имеются и такие, у которых эта вторая координата превышает соответствующую координату рабочей точки.

Смысл, заложенный в данную классификацию, состоит в том, что, согласно принципу причинности, на формирование отклика физически осуществимого фильтра не могут оказывать влияния элементы входного сигнала, не поступившие к моменту формирования выходного отсчета. Этот принцип естественным образом «работает» в динамических системах, где все происходящие в них процессы являются временными процессами.

При цифровой обработке изображений часто приходится иметь дело с ранее сформированными изображениями, уже хранящимися в памяти устройства обработки. В этом смысле соотношение координат, строго говоря, уже не играет такой принципиальной причинной роли, как при обработке сигналов в реальном масштабе времени. Вместе с тем, традиционно сложилась описанная выше классификация процедур обработки изображений, которой, в определенной мере, будем придерживаться и мы в последующем изложении.

При линейной фильтрации выходной эффект определяется линейной комбинацией входных данных:

. (3.2)

В этом выражении

- результат фильтрации полезного сигнала

в точке кадра с координатами

;

- множество точек (точнее - множество их координат), образующих окрестность;

- весовые коэффициенты, совокупность которых представляет собой двумерную импульсную характеристику (ИХ). Если область

конечна, то импульсная характеристика имеет конечную длину и фильтр называется КИХ-фильтром. В противном случае импульсная характеристика имеет бесконечную длину, а фильтр название БИХ-фильтра. В выражении (3.2) принято, что ИХ не зависит от координат точки

, в которой определяется выходной эффект. Процедуры обработки изображений, обладающие свойством независимости от координат, называются однородными.

Наиболее распространенным критерием оптимальности, применяемым для оценки качества обработки, является критерий минимума среднего квадрата ошибок. Применительно к фильтрации запишем его выражение в виде:

, (3.3)

где

- символ математического ожидания. Согласно (3.3) отыскание оптимального фильтра заключается в определении его ИХ таким образом, чтобы средний квадрат ошибки

, выражающей различие между сигналом

и оценкой

, формируемой фильтром, был минимальным. Математическое ожидание вычисляется по всем случайным величинам, содержащимся в (3.3), что означает ориентацию критерия на учет средних ошибок.

Оптимизационную задачу (3.3) нетрудно свести к решению уравнения или системы уравнений.

Для этого вычислим производную от левой части этого выражения по коэффициенту

и приравняем ее нулю. Учитывая, что операции дифференцирования, суммирования и математического ожидания являются линейными и поэтому перестановочны, приходим к выражению:

. (3.4)

Входящие в него математические ожидания являются, как нетрудно видеть, отсчетами корреляционных функций, для которых введем следующие обозначения:

.

С их учетом (3.4) примет более компактный вид:

(3.5)

Считая автокорреляционную

и взаимно корреляционную

функции известными, замечаем, что (3.5) представляет собой линейное относительно искомых коэффициентов

алгебраическое уравнение. Число неизвестных в этом уравнении равняется числу точек

в окрестности

и является конечным в случае КИХ-фильтра и бесконечным при БИХ-фильтрации. Ограничимся в данном параграфе рассмотрением КИХ-фильтрации. Линейное алгебраическое уравнение со многими неизвестными имеет бесконечное множество решений. Если повторить дифференцирование (3.3) по остальным

неизвестным, то получим еще

уравнений, отличающихся друг от друга левыми частями

и коэффициентами

в правых частях, т.к. определяющие их корреляции вычисляются каждый раз в различных точках. В результате образуется система

линейных алгебраических уравнений с

неизвестными, называемая в теории фильтрации уравнением Винера-Хопфа:

(3.6)

Если разрешить ее относительно всех

неизвестных

, то будет найдена искомая импульсная характеристика линейного фильтра, минимизирующего средний квадрат ошибок фильтрации.

Определим средний квадрат ошибок оптимальной фильтрации. Для этого необходимо выполнить возведение в квадрат в выражении (3.3) и учесть в полученном выражении уравнение Винера-Хопфа (3.6). В результате нетрудно получить:

, (3.7)

где

- средний квадрат ошибок фильтрации.

Остановимся на анализе изменения средней яркости изображения при его фильтрации.

Вычислив математическое ожидание от обеих частей (3.2), находим:

, (3.8)

где принято, что средняя яркость

входного изображения

не зависит от координат и, как результат, получено, что и средняя яркость

выходного изображения

также постоянна во всех точках кадра. Очень часто при обработке стремятся сохранить среднюю яркость изображения. Как следует из полученного выражения, достичь этого удается при выполнении равенства

, (3.9)

которое является дополнительным требованием к импульсной характеристике фильтра. Поэтому оптимизационную задачу (3.3) необходимо решать с учетом данного ограничения типа равенства.

Вместо этого часто перед фильтрацией осуществляют вычитание средней яркости

из входного изображения. Как следует из (3.8), среднее значение яркости на выходе фильтра при этом также равно нулю независимо от свойств импульсной характеристики. Это позволяет решать систему уравнений (3.6), игнорируя преобразование средней яркости. Желаемое же ее значение восстанавливается после фильтрации простым прибавлением к выходному эффекту.

3.2. Масочная фильтрация изображений

при наличии аддитивного белого шума

Распространенным видом помехи является белый шум, аддитивно воздействующий на изображение. Наблюдаемое в этом случае изображение (3.1) имеет вид:

, (3.10)

а корреляционная функция шума

описывается выражением:

.

Здесь

- дисперсия шума, а

- символ Кронекера. Считаем, что входной сигнал центрирован, т.е. имеет нулевое математическое ожидание, а изображение

и шум

взаимно независимы, поэтому для корреляционной функции входного сигнала справедливо:

,

где

- дисперсия, а

- нормированная корреляционная функция полезного сигнала. Нетрудно видеть, что в этих условиях взаимная корреляционная функция

совпадает с корреляционной функцией полезного сигнала

. Поэтому уравнение Винера -Хопфа (3.6) приводится к виду:

, (3.11)

где

- отношение дисперсий сигнала и шума.

Преобразуем также выражение (3.7) для ошибок фильтрации, для чего запишем в явном виде то из уравнений в (3.11), которое соответствует значениям

, откуда находим:

. Сравнивая это соотношение с (3.7), окончательно получаем:

,

где

- относительный средний квадрат ошибок фильтрации. Таким образом, для определения ошибок фильтрации необходимо знать отношение сигнал/шум (которое входит также и в уравнение Винера-Хопфа) и значение оптимальной импульсной характеристики в точке (0,0).

Для того чтобы при решении уравнения (3.11) воспользоваться существующими программными средствами ЭВМ, необходимо выполнить его упорядоченное преобразование к каноническому векторно-матричному виду. Для этого требуется совокупность

неизвестных величин

представить в виде вектора

. Точно также множество величин, образующих левые части (3.11), следует представить в виде вектора

, а множество коэффициентов правой части в виде матрицы

размера

. Тогда уравнение и его решение примут вид:

.

В практике цифровой обработки изображений широко используется масочная фильтрация. Ее линейная разновидность является одним из вариантов двумерной КИХ-фильтрации. В качестве маски используется множество весовых коэффициентов, заданных во всех точках окрестности

, обычно симметрично окружающих рабочую точку кадра. Распространенным видом окрестности, часто применяемым на практике, является квадрат 3

3 с рабочим элементом в центре, изображенный на рис. 3.1.б. Применяют различные разновидности масок, одним из эвристических вариантов является равномерная маска, все девять весовых коэффициентов которой равны 1/9. Такой выбор коэффициентов отвечает условию сохранения средней яркости (3.9) и поэтому в процессе обработки центрировать изображение не требуется.

Визуально эффективность фильтрации можно оценить с помощью рис.3.2. На рис. 3.2.а показан зашумленный портрет (изображение без шума приведено на рис. 1.3.а) при отношении сигнал/шум равном -5дБ.

Результат масочной фильтрации при оптимальном виде ИХ, найденной из (3.11), приведен на рис.3.2.б. Результат фильтрации, выполненной равномерным масочным оператором не приводится, поскольку с визуальной точки зрения он мало отличается от рис.3.2.б. При этом, однако, с количественной точки зрения различия достаточно заметны: если при оптимальной КИХ относительная ошибка

, то при равномерной КИХ она возрастает почти на 30% и составляет

. Различие резко возрастает при более высоком уровне шума. Так, например, при отношении сигнал/шум равном -10дБ имеем

, т.е. применение равномерной КИХ вместо оптимальной приводит в этом случае к увеличению ошибок более чем вдвое.


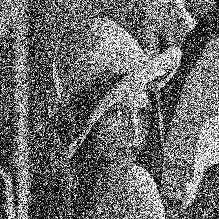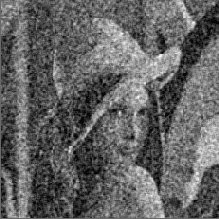а)	б)
Рис. 3.2. П.ример масочной фильтрации при

Здесь полезно отметить определенное разногласие в оценках качества, даваемых человеческим глазом и применяемыми количественными показателями. Глаз является слишком совершенным изобретением природы, чтобы с ним могли соревноваться достаточно примитивные математические показатели типа среднего квадрата ошибок. Поэтому некоторые результаты, рассматриваемые с точки зрения математических показателей как катастрофические, визуально могут быть вполне удовлетворительными. Означает ли это, что математические критерии вообще непригодны при цифровой обработке изображений? Конечно, нет. Цифровая обработка изображений находит применение в различных информационных системах с автоматическим принятием решений, основанным на этой обработке.

Функционирование таких систем, где отсутствует человеческий глаз, полностью подчинено математическим критериям и качество их работы оценивается только математическими показателями. Понятно, что и качество изображений, используемых в этих системах, также должно оцениваться только математическими критериями.

В заключение данного параграфа подчеркнем, что в целом применение описанных процедур фильтрации приводит к существенному снижению уровня шума на изображении. Количественно эффективность данной обработки можно охарактеризовать коэффициентом улучшения отношения сигнал/шум

, где учтено, что величина

определяет отношение сигнал/шум после фильтрации.

Улучшение зависит от уровня шума на исходном изображении и составляет в приведенном эксперименте

при

дБ и

при

дБ. Коэффициент улучшения тем выше, чем сильнее шум на исходном изображении.

3.3. Рекуррентная каузальная фильтрация изображений

          Проблема борьбы с шумом не решается полностью применением масочных фильтров по следующим причинам. Во-первых, ограниченность размера окрестности, используемой масочным фильтром, приводит к его потенциально ограниченной способности к подавлению шума. Это проявляется при значительном уровне шума на изображении - в меньшей степени при оптимальном выборе КИХ, сильнее при неоптимальной КИХ. Можно, конечно, увеличивать размер окрестности, прибегая к использованию КИХ-фильтров с более длинными импульсными характеристиками. Однако при этом усиливается второй недостаток масочного фильтра, состоящий в его и без того достаточно высокой вычислительной трудоемкости.

В настоящее время отсутствуют методы двумерной фильтрации, в которых сочетаются предельно достижимое качество фильтрации и низкие требования к вычислительным ресурсам ЭВМ, реализующей обработку. Существует много подходов к решению данной проблемы, но все они для достижения компромисса между точностью и реализуемостью прибегают к тем или иным приближениям. Рассмотрим один из них [3.1].

          Идея заключается в использовании двумерного БИХ-фильтра с таким видом импульсной характеристики, при которой его практическая реализация была бы простой, и с такими параметрами этой импульсной характеристики, при которых эффективность фильтрации приближалась бы к потенциально возможной. Создать фильтр с такими свойствами удается на основе аналогии с одномерным фильтром Калмана.

          Наиболее простым примером одномерной фильтрации является калмановская фильтрация однородной стационарной гауссовской последовательности, имеющей корреляционную функцию экспоненциального вида

.

Здесь

- дисперсия последовательности, а

- коэффициент ее одношаговой корреляции, определяемый параметром

, имеющим смысл ширины спектра последовательности.

При ее наблюдении на фоне гауссовского белого шума оптимальный каузальный фильтр реализуется рекуррентным алгоритмом, который в стационарном (установившемся) режиме фильтрации имеет вид:

. (3.12)

Нетрудно установить, что импульсная характеристика этого фильтра имеет экспоненциальный вид:

, (3.13)

где

- параметр, лежащий в пределах

, и получивший название коэффициента усиления фильтра Калмана. Первое слагаемое в алгоритме (3.12) определяет вклад в оценку сигнала на текущем

-м шаге фильтрации, вносимый оценкой предыдущего шага, и называется одношаговым прогнозом. Второе учитывает влияние текущего наблюдения

и называется новой информацией. Коэффициент усиления

определяет чувствительность фильтра к этой новой информации. При высоком уровне шума параметр

приближается к нулю. При этом, кроме общего снижения ИХ, увеличивается параметр

, приближаясь к единице. Это означает удлинение импульсной характеристики и, следовательно, сужение полосы пропускаемых фильтром частот. Очевидно, эти свойства ИХ способствуют эффективной фильтрации шума. При снижении шума, наоборот,

стремится к единице,

- к нулю, что соответствует расширению полосы частот до бесконечности. Здесь уместно отметить, что фильтрация не только ослабляет действие шума, но, к сожалению, и вносит так называемые динамические искажения в полезный сигнал. Механизм этих искажений очень прост и заключается в неравной передаче на выход фильтра различных спектральных компонент сигнала. Фильтр Калмана “ведет себя” вполне разумно, когда при исчезновении шума на входе расширяет полосу пропускаемых частот до бесконечности, поскольку именно при этом условии исчезают и динамические ошибки фильтрации.

Отталкиваясь от (3.13) как от одномерного аналога, будем находить двумерную БИХ для каузальной фильтрации изображений от некоррелированного шума в виде двумерной экспоненты:

. (3.14)

Здесь, как и в случае одномерного фильтра,

- коэффициент одношаговой корреляции изображения по строке и по столбцу, которые будем здесь считать одинаковыми.

Для определения параметра

(или

), остающегося единственным неизвестным параметром двумерного фильтра, воспользуемся уравнением Винера-Хопфа в форме (3.4), переписав его в виде:

.

Замечая, что выражение в круглых скобках является ошибкой фильтрации, представим эту формулу в виде:

. (3.15)

Смысл данного выражения состоит в том, что при оптимальной линейной фильтрации ошибка ортогональна всем элементам наблюдаемых данных, используемых при фильтрации. Но тогда нетрудно убедиться и в ортогональности ошибки и результата фильтрации (получаемой оценки)

, (3.16)

для чего достаточно вычислить левую часть этого выражения с учетом (3.2) и (3.15).

Для дальнейшего необходимо воспользоваться в (3.16) принятым представлением импульсной характеристики (3.14), в результате данное соотношение превращается в уравнение относительно искомого параметра

. В него входят корреляционная функция сигнала и взаимно-корреляционная функция сигнала и наблюдаемых данных. Поэтому необходимо конкретизировать корреляционную функцию сигнала, в качестве которой воспользуемся биэкспоненциальным представлением:

. (3.17)

С учетом этого, считая, что кадр имеет бесконечные размеры (это позволяет принять бесконечными соответствующие пределы суммирования в (3.2)), можно получить следующее алгебраическое уравнение

(3.18)

относительно параметра

, численное решение которого не представляет проблемы. Анализируя (3.18), легко заметить, что при

это уравнение

удовлетворяется при

, а при

его решением является

. Эти предельные значения можно интерпретировать как изменения частотно-полосовых характеристик двумерного фильтра, аналогичные поведению параметров фильтра Калмана в подобных предельных ситуациях.

Подставив в (3.7) выражения ИХ (3.14) и корреляционной функции (3.17), можно получить следующую формулу для среднего квадрата ошибок фильтрации:

.

Подставив далее выражение ИХ (3.14) в (3.2), можно привести выражение отклика фильтра к виду :

. (3.19)

Рекуррентный характер алгоритма (3.19) является важным положительным качеством рассматриваемого фильтра. Как следует из (3.19), его работа требует выполнения на каждом шаге обработки всего трех операций умножения и трех суммирования, причем структура алгоритма универсальна и, в частности, не зависит от отношения сигнал/шум. Для сравнения, масочный фильтр с размером окрестности 3

3 элементов требует выполнения на каждом шаге при общем виде КИХ девяти умножений и восьми суммирований. Таким образом, по количеству операций рекуррентный фильтр выигрывает у простейшего масочного практически в три раза. Очевидно, что попытка улучшить качество фильтрации масочным фильтром за счет увеличения размера применяемой окрестности приводит к увеличению числа операций и дальнейшему увеличению его проигрыша по этой характеристике.

При фильтрации реальных изображений ограниченного размера возникает граничная проблема получения оценок в точках нулевой строки и нулевого столбца. Естественным решением является использование здесь обычной (одномерной) калмановской фильтрации.

Пример применения описанного двумерного фильтра показан на рис. 3.3, где представлен результат эксперимента с тем же портретом и при том же отношении сигнал/шум -5 дБ, что и при испытании масочного фильтра.


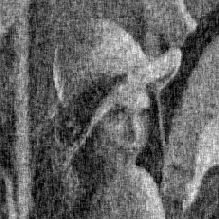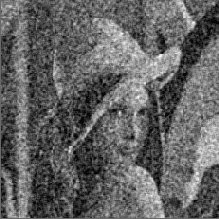а)	б)
Рис. 3.3. Пример двумерной рекуррентной фильтрации

Поэтому здесь не приводится показанное на рис.3.2.а входное изображение с шумом. Результат двумерной рекуррентной фильтрации представлен на рис.3.3.а, а на рис.3.3.б для сравнения повторен результат оптимальной масочной фильтрации (рис.3.2.б). Визуальная оценка говорит в пользу двумерного рекуррентного фильтра, поскольку уровень остаточного шума на рис.3.3.а ниже. Сравнение по среднему квадрату ошибок совпадает с субъективной оценкой: величина

при масочной фильтрации составляет, как говорилось ранее, 0.309, а при двумерной рекуррентной - 0.29.

Различие заметно усиливается при более высоком уровне шума. Так, при отношении сигнал/шум -10 дБ имеем соответственно

  равным 0.57 и 0.43.

          Необходимо отметить, однако, следующее. Вместе с уменьшением уровня шума при двумерной рекуррентной фильтрации наблюдается более значительная утрата резкости обработанного изображения. Это является проявлением упоминавшихся выше динамических искажений, более сильных при бесконечной импульсной характеристике, чем при конечной.

          Во-вторых, рассмотренный двумерный фильтр не является абсолютно оптимальным, поскольку его структура определена волевым решением при выборе ИХ в виде (3.14). Поэтому и получаемое при его помощи ослабление шума не является предельным.

3.4. Применение фильтра Винера для некаузальной

двумерной фильтрации

          Потенциально наилучшие результаты обработки изображения, в частности, результаты фильтрации, достигаются при использовании некаузального принципа, поскольку этот принцип основан на применении абсолютно всех исходных данных при обработке каждой точки кадра. Понятно, что при рациональном использования этих данных получаемый эффект максимален. Одним из известных вариантов линейной некаузальной фильтрации изображений является фильтр Винера. Его применение связано с предположением о стационарности изображения. Поскольку наличие краев изображения служит нарушением стационарности, то винеровская фильтрация, не является строго оптимальной. Однако при размерах кадра, значительно превышающих интервал корреляции изображения, влияние границ является малым. Эти соображения служат важным стимулом к применению винеровской фильтрации для борьбы с шумом.

          Технически фильтр Винера реализуется при помощи дискретного преобразования Фурье в частотной области. Поэтому, прежде чем рассматривать уравнение Винера-Хопфа, которое остается методологической основой фильтрации помех и в этом случае, нам необходимо познакомиться с двумерным дискретным преобразованием Фурье (ДПФ), некоторыми его свойствами и принципами линейной фильтрации на основе ДПФ.

3.4.1. Двумерное дискретное преобразование Фурье

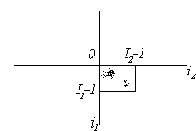
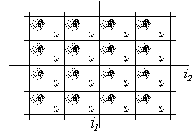
          Обозначим через

(3.20)

двумерное поле (двумерный сигнал), описывающее дискретное изображение размера

строк и

столбцов. Вне указанных границ этот сигнал не определен. Выполним периодическое продолжение данного финитного сигнала, введя двумерный периодический сигнал

. (3.21)

Если сигнал

существует только внутри прямоугольника

со сторонами

элементов


а)	б)
Рис. 3.4. Реальное (а) и периодически продолженное (б) изображения

(рис. 3.4.а), то сигнал

определен на всей плоскости

и является на ней прямоугольно-периодическим (рис. 3.4.б).

Любой периодический сигнал может быть представлен в виде ряда Фурье, но, в отличие от одномерных сигналов, двумерные описываются двумерным рядом Фурье, имеющим вид:

. (3.22)

Базисные функции этого двумерного представления - двумерные комплексные экспоненты (иногда называемые комплексными синусоидами)

, (3.23)

имеющие, как и сигнал

, прямоугольную периодичность с тем же периодом

. Здесь (

) - двумерный номер базисной функции, а величины

имеют смысл пространственных частот. Иногда пространственными частотами называют целочисленные величины

.

Коэффициенты Фурье

ряда (3.22) образуют двумерный частотный спектр сигнала

и определяются формулой прямого преобразования Фурье:

(3.24)

Выражение (3.22), восстанавливающее сигнал

по его спектру

, является обратным преобразованием Фурье. В справедливости преобразований (3.22) и (3.24), называемых двумерным ДПФ, можно убедиться, подставив (3.24) в (3.22) и приведя правую часть полученного равенства к значению левой, т.е. к

.

Заметим, что для точного представления дискретного сигнала

с двумерным периодом

элементов согласно формулам БПФ достаточно конечного числа базисных функций (3.23) - ряд (3.22) является конечным.

Это и понятно, поскольку сам представляемый сигнал содержит в одном периоде конечное число точек, т.е. имеет конечное число степеней свободы. Ясно, что число степеней свободы в спектре не может отличаться от числа степеней свободы в самом сигнале.

Остановимся на наиболее существенных свойствах двумерного дискретного спектра Фурье. Вычислим спектральные коэффициенты (3.24) в частотных точках

(3.25)

Поскольку при любых целых значениях

последний множитель в полученном выражении равен единице, то отсюда имеем равенство:

,

означающее прямоугольную периодичность двумерного ДПФ. Следовательно, картина двумерного ДПФ подобна картине двумерного периодически продолженного сигнала, качественно показанной на рис. 3.4.б (если на ней пространственные координаты

заменить частотными

). Однако необходимо иметь в виду, что спектральные коэффициенты

, как это следует из (3.24), являются комплексными числами, в том числе и при вещественном сигнале

. Но тогда возникает вопрос. Общее количество спектральных компонент, как установлено, равно

. Комплексное число эквивалентно паре вещественных чисел - действительной и мнимой частям при алгебраическом или модулю и фазе при экспоненциальном представлении. Следовательно, полный спектр описывается

вещественными числами, что вдвое превышает размерность самого сигнала

. В этом, на первый взгляд, содержится противоречие. Оно находит свое разъяснение при дальнейшем изучении свойств двумерного ДПФ.

Преобразуем соотношение (3.25) следующим образом. Во-первых, вместо частот

подставим частоты

. Во-вторых, выполним комплексное сопряжение обеих частей, что не нарушит равенства. В результате нетрудно получить выражение:

,

которым устанавливается однозначная связь между спектральными коэффициентами в двух различных точках спектрального прямоугольника

. Полученным соотношением и снимается противоречие, поскольку количество независимых спектральных коэффициентов уменьшается благодаря данной спектральной симметрии в два раза.

Согласно установленному свойству, спектрально- сопряженной зависимостью связаны между собой спектральные коэффициенты, принадлежащие левому верхнему и правому нижнему углам прямоугольника

. Аналогично также связаны между собой коэффициенты Фурье из правого верхнего и левого нижнего участков спектрального прямоугольника

.

В заключение данного пункта укажем, что при практическом применении двумерного ДПФ - как прямого, так и обратного, совсем не требуется оперировать периодическими сигналами и спектрами, как это предполагается, казалось бы, преобразованиями (3.22) и (3.24). От этой необходимости избавляют сами соотношения (3.22) и (3.24). В самом деле, прямое преобразование Фурье (3.24) содержит в правой части значения периодически продолженного сигнала

лишь в пределах одного “главного” прямоугольника

. Но в этих пределах исходный

и периодически продолженный

сигналы полностью совпадают, что дает возможность использовать в формуле (3.24) исходный сигнал

. Аналогичные пояснения можно сделать и относительно обратного преобразования (3.22), откуда следует, что практически в процессе вычислений оперировать следует “основным” участком спектра, относящимся к спектральной области

.

Из сделанных пояснений, имеющих лишь исключительно вычислительное значение, не следует делать вывода об искусственности и ненужности рассмотренных математических моделей периодических полей. При обработке изображений возникают многочисленные задачи, правильное толкование и решение которых возможно только на основе этих математических интерпретаций. Одной из таких важнейших задач является цифровая двумерная фильтрация в спектральной области, осуществление которой связано с выполнением так называемой циклической свертки.

3.4.2. Циклическая свертка

Достоинством обычного преобразования Фурье является то, что с его помощью очень просто выполняется стационарная фильтрация сигналов. Как известно, для этого требуется получить частотный спектр сигнала и частотный коэффициент передачи фильтра.

Затем, перемножив их, определить частотный спектр выходного сигнала, а выполнив обратное преобразование Фурье - найти сам выходной сигнал. Возможно ли применение такой технологии для выполнения двумерной цифровой фильтрации ? Убедимся, что возможно, но с некоторыми оговорками.

Двумерный стационарный (инвариантный к сдвигу) фильтр характеризуют двумерной импульсной характеристикой

, позволяющей определить выходной сигнал при помощи двумерной свертки:

. (3.26)

Это уравнение обычной свертки, в нем фигурируют обычные, непериодические сигналы и непериодическая ИХ фильтра. При цифровой обработке в ЭВМ не существует частотных спектров, соответствующих таким сигналам и ИХ. Для описания сигнала в частотной области привлекается, как установлено выше, периодически продолженный сигнал

, которому соответствует дискретный спектр

. По аналогии с (3.21) вводится и периодически продолженная ИХ:

,

двумерное ДПФ которой

имеет смысл частотного коэффициента передачи цифрового фильтра. Покажем, что перемножая

, мы находим спектр сигнала, определяемого циклической сверткой. Циклическая свертка отличается от обычной свертки (3.26) тем, что вместо функций

в ней представлены периодически продолженные функции

. Нетрудно установить, что при этом сигнал на выходе

. (3.27)

также является периодическим. Покажем, что именно его спектр

определяется выражением:

. (3.28)

Умножим для этого левую и правую части (3.27) на

и просуммируем по

в пределах области

. В левой части в результате имеем спектр

. Преобразуем правую часть, предварительно умножив ее на величину

, тождественно равную единице:

.

Выполняя затем во внутренней сумме замену переменных

, учитывая, что при суммировании периодической функции в пределах периода границы суммирования могут быть синхронно сдвинуты на любую величину и оставляя их в этой связи неизменными, приходим к (3.28).

Таким образом установлено, что именно циклической свертке (3.27) соответствует удобный при практической реализации частотный метод определения выходного сигнала. Необходимо иметь в виду, что та фильтрация, к осуществлению которой обычно стремятся при решении конкретных задач, описывается обычной сверткой (3.26), а не циклической (3.27). Поэтому остается выяснить, в каком соотношении находятся эти две вычислительные процедуры. Не нарушая общности, для большей простоты и наглядности рассмотрим этот вопрос на примере одномерной фильтрации. Сигнал на выходе одномерного фильтра определяется сверткой

, (3.29)

(3.30)

в обычном и циклическом вариантах соответственно. Рис. 3.5 поясняет процесс


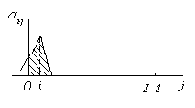а)	б)	в)
Рис. 3.5. Сравнение обычной и циклической свертки

вычисления выходного сигнала в обоих случаях. На рис. 3.5.а показана импульсная характеристика произвольного вида, соответствующая некаузальному фильтру (т.к.

при

). Рис. 3.5.б иллюстрирует образование суммы, вычисляемой при помощи обычной свертки (3.29), а рис. 3.5.в при помощи циклической (3.30). На рисунках штриховкой показаны области суммирования, выполняемого в соответствии с выражениями (3.29) и (3.30). Рисунки отражают определение реакции фильтра в точке

, расположенной вблизи границы рабочей области. В случае циклической свертки область суммирования является двухсвязной из-за периодичности ИХ, что приводит к различию результатов фильтрации. Очевидно, что эффекты, вызванные периодичностью, отсутствуют для точек, удаленных от границ. Поэтому для внутренних точек области

, удаленность которых от границ превышает длину импульсной характеристики, результаты обычной и циклической сверток совпадают. Различия наблюдаются лишь для точек, примыкающих к границе. Если размеры этой приграничной области относительно невелики, то часто различиями пренебрегают. В тех случаях, когда граничные эффекты недопустимы, проблема может быть разрешена при помощи искусственного удлинения области

добавлением к ней на обоих концах такого количества нулевых элементов, при котором эффект цикличности проявляться не будет.

В заключение отметим, что характер различий обычной и циклической сверток при фильтрации двумерных цифровых сигналов остается таким же, как для одномерных сигналов. Аналогичны и меры, исключающие нежелательные эффекты циклической свертки.

3.4.3. Решение уравнения Винера-Хопфа в циклическом приближении

Вернемся к задаче некаузальной фильтрации шума на изображении. Оптимальный линейный фильтр определяется и в этом случае уравнением Винера-Хопфа (3.6), в котором для начала область существования

импульсной характеристики примем неограниченной. В результате имеем:

(3.31)

Дискретный винеровский фильтр удается легко найти в циклическом приближении. Для этого требуется вместо реальных функций

подставить в уравнение (3.31) соответствующие периодически продолженные функции

, имеющие двумерный период

. При этом область определения ИХ также сужается до размеров прямоугольника

. Поэтому (3.31) принимает вид:

(3.32)

Периодичность функций, входящих в уравнение (3.32), позволяет применить к его обеим частям двумерное ДПФ, подобно тому, как это было сделано выше применительно к уравнению (3.27). В результате получаем:

. (3.33)

В этом выражении

- спектральные плотности мощности, представляющие собой ДПФ соответствующих корреляционных функций, а

- ДПФ искомой импульсной характеристики, являющееся, таким образом, частотным коэффициентом передачи фильтра Винера. Все функции, входящие в (3.33), являются прямоугольно-периодичными с двумерным периодом

. Основное достижение, вызванное применением ДПФ, состоит в преобразовании сложного для решения уравнения Винера-Хопфа (3.32) в простейшее алгебраическое уравнение (3.33), решение которого, правда не для импульсной, а для частотной характеристики, имеет вид:

. (3.34)

Найденное решение дает эффективный способ осуществления оптимальной линейной фильтрации изображения.

Его выполнение требует знания спектральных плотностей мощности и опирается на применение к обрабатываемому изображению дискретного преобразования Фурье.

Не следует, однако, забывать, что переход от уравнения (3.31), определяющего истинно оптимальную характеристику фильтра, к уравнению (3.32), позволяющему найти ее периодически продолженный аналог, был выполнен без достаточного обоснования. Поэтому ничего нельзя пока сказать о том, в какой степени найденное решение близко к истинно оптимальному. Для ответа на этот вопрос рассмотрим снова для простоты одномерные аналоги уравнений (3.31) и (3.32), имеющие вид:

(3.35)

(3.36)

Рис. 3.6 иллюстрирует формирование сумм, входящих в правые части этих равенств при некотором произвольном значении сдвига

и достаточно большом значении интервала наблюдения

. Здесь показаны некаузальная ИХ и корреляционная функция входного сигнала, а штриховкой условно отмечена область суммирования. Из сравнения рис. 3.6.а, соответствующего (3.35), и рис. 3.6.б, соответствующего (3.36), видно, что, хотя во втором случае область суммирования и является двухсвязной, это не приводит к различию результатов


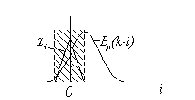а)	б)
Рис. 3.6. Сравнение обычного и циклического уравнений Винера-Хопфа

суммирования. При большом значении длины интервала

соседние зоны на рис. 3.6.б не перекрываются, благодаря чему искажения результатов не происходит. Следовательно, уравнения (3.35) и (3.36) являются эквивалентными.

Если же интервал

будет соизмерим с размахом корреляционной функции

, то произойдет наложение соседних областей периодической картины, что в итоге приведет к изменению значений функций, стоящих под знаком суммы в (3.36), и исказит уравнение Винера-Хопфа. Таким образом, условие применимости фильтра Винера, определяемого соотношением (3.34), состоит в его использовании для обработки изображений, имеющих достаточно большие размеры.

Напомним также, что в данном пособии обсуждается уравнение Винера-Хопфа для стационарных сигналов и изображений. Поэтому вблизи границ обрабатываемого кадра, где само их существование приводит к нарушению этого условия, обработка отклоняется от оптимальной.

На рис. 3.7 приведен пример работы фильтра Винера. Как и ранее эксперимент выполнен при отношении сигнал/шум

. Относительный средний квадрат ошибок фильтрации

составляет в этом эксперименте величину 0,167, что является наилучшим показателем среди всех рассмотренных методов линейной фильтрации (напомним, что при масочной фильтрации выше было получено

, а при рекуррентной

). О наименьшем уровне остаточного шума на изображении говорит и визуальная

оценка результата. Хотя нельзя не отметить, что это достигается ценой большей, чем при других методах, дефокусировки изображения. В этом проявляется общее диалектическое противоречие между борьбой с помехами и


а)	б)
Рис. 3.7. Пример винеровской фильтрации шума при

динамическими искажениями обрабатываемого изображения, свойственное, как отмечалось и ранее, всем методам фильтрации.

Проведение обработки изображений при помощи фильтра Винера требует использования спектральной плотности мощности изображения. Существуют различные способы получения необходимой информации. Один из них основан на предварительном измерении требуемых характеристик по реальному изображению. Полученные при этом спектральные плотности вводятся в ЭВМ в виде таблиц, позволяя задать коэффициент передачи в численном виде. Другой способ, примененный и в представленном эксперименте, состоит в использовании некоторой математической модели изображения, вид спектрально-корреляционных характеристик которой известен. В этом случае реальное изображение используется для измерения только отдельных параметров, входящих в используемую математическую модель. При проведении эксперимента, описанного выше , в частности, использовалась модель изображения в виде гауссовского двумерного поля с корреляционной функцией (3.17), а измерялись коэффициент одношаговой корреляции

и дисперсия

.

Анализ эффективности метода будет неполным, если не сделать оценки вычислительной эффективности реализующей его процедуры. Для вычисления ДПФ разработаны эффективные вычислительные методы, воплощенные в процедурах быстрого преобразования Фурье (БПФ). Количество комплексных умножений, составляющих основную трудоемкость двумерного БПФ, оценивают числом

[3.2]. Поскольку полный цикл обработки предполагает выполнение прямого и обратного БПФ, то это число следует удвоить. По отношению к одному элементу кадра число умножений, таким образом, составляет

. При

число умножений в каждой точке кадра равно 32. Для сравнения напомним, что, например, рекуррентный двумерный фильтр, описанный выше, реализуется всего тремя вещественными умножениями в каждой точке кадра (при различных значениях одношагового коэффициента корреляции изображения по строкам и по столбцам - четырьмя умножениями).

3.5. Байесовская фильтрация изображений

          При всех рассмотренных ранее методах фильтрации с самого начала закладывалось отыскание фильтра в классе линейных систем. Отсюда следует, что могут существовать нелинейные процедуры, обладающие более высокими качественными характеристиками, чем рассмотренные выше. Для их отыскания необходим более общий подход к фильтрации, чем тот, который опирается на решение уравнение Винера-Хопфа. Общепринятая достаточно универсальная идеология фильтрации использует байесовский принцип. Ее применение позволяет, по крайней мере теоретически, создавать как линейные, так и нелинейные алгоритмы фильтрации. Кроме того, этот принцип помогает выяснить, при каких условиях линейные процедуры фильтрации приводят к наивысшему качеству обработки и, следовательно, являются абсолютно оптимальными.

          Отметим, однако, с самого начала основные недостатки байесовской фильтрации изображений. Первый является общим для байесовских методов вообще и заключается в очень высоких требованиях к объему и характеру данных, содержащихся в математических моделях сигналов и помех, удовлетворить которым на практике удается далеко не всегда.

Второй связан со спецификой изображений как двумерных сигналов, что приводит к колоссальным вычислительным трудностям при попытке прямого использования этого подхода. Последнее делает актуальной разработку таких методов, которые способны преодолеть данное ограничение. Достичь этого обычно удается ценой определенной потери качества обработки. Поэтому дело сводится к поиску таких методов, при которых потеря качества являлась бы приемлемой.

3.5.1. Сущность байесовской фильтрации

          Полагаем, что на входе фильтра действует сигнал

, (3.37)

где

- полезный сигнал и помеха, а

- функция, описывающая их взаимодействие. При байесовском методе считается, что сигнал и помеха - случайные процессы (случайные двумерные поля) с известными законами распределения вероятностей. Пусть

- вектор, элементы которого - все

отсчетов, образующих кадр изображения, а

-их совместное распределение. Примем для простоты, что помеха и сигнал независимы, а распределение вектора помехи

равно

. Воспользовавшись формулой Байеса, запишем апостериорное распределение вероятностей (АРВ)

, (3.38)

куда входит распределение

наблюдаемых данных и условное распределение

- называемое функцией правдоподобия. Смысл выражения (3.38) заключается в том, что оно дает возможность вычислить в устройстве обработки распределение вероятностей полезного сигнала, располагая входными данными

и опираясь на вероятностную модель как самого полезного сигнала, так и наблюдаемых данных. АРВ является аккумулятором всех доступных сведений о полезном сигнале, которые содержатся в

, а (3.38) указывает способ извлечения этих сведений.

Поскольку потребителя информации обычно интересует точечное значение сигнала

, то для его образования прибегают к вычислению либо математического ожидания АРВ, либо его координаты, обращающей это распределение в максимум. В математической статистике доказано, что эти способы получения результатов фильтрации соответствуют различным содержательным требованиям, предъявляемым к получаемым результатам [3.3].

Оперировать векторными величинами, входящими в (3.38), практически невозможно из-за громадной размерности векторов

. Если, например, обрабатываемый кадр имеет размеры

, то размерность этих векторов равна

. Предположим, что изображение является простейшим с бинарными значениями элементов

. Общее число всевозможных изображений, имеющих всего две градации яркости, составляет

. Задачей байесовского фильтра является вычисление распределения вероятностей

, которое можно представить себе в данном случае в виде таблицы с размером, превышающим

. Явная нереальность этой задачи заставляет искать такие методы описания сигналов, которые приводили бы к резкому, качественному ее упрощению. В данном направлении предпринимаются усилия, разрабатываются различные подходы [3.4-3.6], но, к сожалению, универсальных эффективных методов двумерной байесовской обработки изображений, основанных на использовании всех данных

, в настоящее время не найдено.

Отмеченная сложность байесовских процедур свойственна и фильтрации одномерных сигналов. Вместе с тем, в области одномерной фильтрации были получены блестящие решения проблемы, основанные на использовании марковских моделей сигналов и помех. В указанных работах [3.4-3.6] предпринимались разнообразные попытки распространить идеи марковской фильтрации на двумерные сигналы. Прежде чем остановиться на одном из методов, развитых в работах [3.6,3.8], рассмотрим кратко одномерную марковскую фильтрацию дискретных сигналов, поскольку она составляет основу двумерных процедур.

3.5.2. Марковская фильтрация одномерных последовательностей

Рассмотрим одномерную задачу фильтрации, когда входные данные представлены в виде одномерной последовательности наблюдений:

(3.39)

Здесь все обозначения имеют тот же смысл, что и в (3.37) для двумерных сигналов. Для пояснения сути марковской фильтрации рассмотрим простейший вариант задачи: будем считать помеху независимым процессом (т.е.

- последовательность случайных независимых чисел), а сигнал - простой марковской последовательностью.

На пояснении последнего остановимся подробнее. Последовательность является марковской, если ее совместное распределение вероятностей может быть представлено в виде:

. (3.40)

Данное выражение содержит в правой части одномерное распределение

для нулевого элемента последовательности и цепочку так называемых одношаговых распределений вероятностей перехода

, представляющих собой разновидность условных распределений. Соотношение (3.40) описывает свойство ограниченного последействия, проявляемое в том, что условное распределение

элемента

зависит лишь от единственного соседнего элемента

. Последовательность как бы “прошита” цепочкой непосредственных соседних связей. Элементы, удаленные друг от друга более чем на один шаг, непосредственным вероятностным механизмом не связаны. Это, впрочем, совсем не означает их независимости, зависимость проявляется опосредованно, через цепочку прямых связей.

Часто индексы

, входящие в (3.40), ассоциируют с дискретным временем, а последовательность

называют случайным процессом. Тогда о соотношении (3.40) говорят, что оно описывает процесс в прямом времени. Известно, что марковский процесс

обладает марковским свойством и в обратном времени, что позволяет записать его распределение вероятностей в виде:

. (3.41)

В соотношение (3.41) входит распределение последнего элемента и цепочка одношаговых распределений перехода в обратном времени

, не совпадающих с

.

Марковские процессы обладают разделяющим свойством, позволяющим представить их распределение еще в одной форме, полезной для разработки оптимальных процедур фильтрации. В соответствии с этим свойством любой элемент последовательности

разделяет ее на два условно независимых множества

, которые при известном значении

условно независимы [3.7], т.е. имеют место равенства:

(3.42)

Последнее соотношение дает возможность построения некаузального фильтра, формирующего результат фильтрации при помощи очень удобных, экономичных вычислительных процедур.

Это является результатом того, что апостериорное распределение вероятностей для произвольного

элемента последовательности может быть представлено в виде [3.7]:

. (3.43)

В правую часть (3.43) входят три частичных АРВ элемента

, различающиеся составом входных данных, на которых основаны эти АРВ. Здесь

- векторы прошлых и будущих данных соответственно, причем оба содержат текущий элемент

. Основанные на них в отдельности АРВ могли бы послужить основой для образования каузальной и антикаузальной оценок полезного сигнала. В знаменателе стоит одноточечное АРВ, компенсирующее двукратное присутствие текущего наблюдения

в числителе, а коэффициент

подбирается так, чтобы обеспечивалась нормировка к единице получаемого АРВ.

Согласно (3.43) получение оценки складывается из двух этапов. На первом этапе из локальных входных данных формируются локальные АРВ, которые на втором этапе объединяются в окончательное АРВ, используемое далее для получения точечной оценки. Вычислительная сложность этого процесса в значительной степени определяется сложностью формирования локальных АРВ, главным образом находящихся в числителе формулы (3.43), т.к. получение одноточечного АРВ в знаменателе обычно является достаточно простой задачей.

Определение локальных АРВ очень сильно облегчается при использовании марковских свойств последовательностей. Оказывается, что они могут вычисляться при помощи рекуррентных соотношений. Так, например АРВ

вычисляется на основе рекуррентного уравнения в прямом времени:

. (3.44)

Здесь

- область интегрирования, определяемая областью значений последовательности

, а

- нормирующий коэффициент. Для вычисления текущего АРВ

необходимо, согласно (3.44), использовать АРВ

, являющееся одним из итогов работы фильтра в предыдущей точке. В удобстве этого выражения для практической реализации и состоит одно из основных преимуществ марковской фильтрации. Наряду с ограниченным объемом вычислений, предписанных (3.44), при работе на каждом шаге не требуется использовать полное множество входных данных, поскольку в выражение (3.44) входит только текущий элемент обработки

.

Аналогично выглядит и рекуррентное соотношение для локального АРВ

с тем лишь отличием, что оно развивается в обратном времени от конца интервала наблюдения к его началу. Оба рекуррентных соотношения должны быть дополнены граничными условиями, определяющими одноточечные АРВ

, что, как упоминалось выше, не представляет сложной задачи.

В целом, процедура фильтрации, основанная на приведенных соотношениях, выглядит следующим образом. Сначала выполняется обработка последовательности в прямом времени, в результате чего во всех точках формируется АРВ

, затем осуществляется развертка в обратном времени, в ходе которой формируются локальные АРВ

. Далее снова осуществляется развертка в прямом (или в обратном) времени, в ходе которой вычисляются одноточечные

и полные

АРВ. Одновременно в каждой точке определяется точечная оценка, например, как координата максимума АРВ. Состав вычислений очень удобен для параллельной реализации. При наличии параллельных вычислительных устройств можно одновременно в различных вычислителях определять различные локальные АРВ и затем в режиме последовательной обработки объединять все локальные результаты. Само это объединение происходит независимо для всех точек последовательности, что позволяет финальную процедуру формирования окончательных точечных оценок выполнять снова параллельно во всех точках.

3.5.3. Двухэтапная марковская фильтрация изображений

Рассмотрим подход к фильтрации изображений, основу которого составляет использование двумерных, но неполных входных данных, а также наличие у них марковских свойств. Рассмотрим получение оценки изображения в произвольной точке кадра с координатами

, называя ее текущей точкой фильтрации. Осуществляя развертку изображения, можно последовательно в состояние текущей точки переводить все точки кадра, выполняя таким образом его полную обработку.

Будем считать, что для получения оценки

в точке

привлекаются лишь данные

, образованные наблюдениями

-й строки и

-го столбца, на пересечении которых в кадре расположен оцениваемый элемент.

Рис. 3.8 иллюстрирует геометрию задачи.

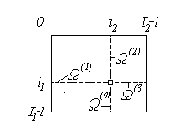Рис. 3.8. Геометрия использования данных при двухэтапной фильтрации

Наблюдения

образованы входными данными, лежащими на горизонтальных и вертикальных лучах

, расходящихся из текущей точки. Причем в каждый из этих векторов не входит текущее наблюдение

, которое в связи с этим представлено в

отдельным элементом.

Будем, кроме того, рассматривать такие случайные поля

, которые обладают свойством условной независимости. Это означает, что совместное распределение всех его элементов

, расположенных на “кресте”

(рис. 3.8), можно представить в виде:

, (3.45)

где верхние индексы также указывают на принадлежность векторов соответствующим лучам. Соотношение (3.45) означает, что значения сигнала на любой строке и на любом столбце изображения условно независимы, если известно значение сигнала

на пересечении этих строки и столбца. Если, кроме того, одномерные сигналы

являются марковскими последовательностями, для которых справедливо свойство условной независимости (3.42), то имеем:

. (3.46)

Используя эту математическую модель изображения в случае независимой помехи

, можно одноточечное апостериорное распределение представить в виде [3.6]:

. (3.47)

Соотношение (3.47) служит теоретической базой для построения оптимальных двухэтапных процедур фильтрации, использующих неполные данные исходных наблюдений. Полное АРВ, основанное на всех привлекаемых при фильтрации данных

, как и в одномерном случае, представляется в виде произведения частных АРВ, каждое из которых использует локальные данные одного из лучей

и текущий элемент

. Наличие в знаменателе третьей степени одноточечного АРВ служит компенсацией трехкратного “лишнего” участия текущего наблюдения в числителе. Константа

позволяет сделать АРВ нормированным.

Рассмотренный вариант обработки является разновидностью некаузальной фильтрации, поскольку в получении оценки участвуют элементы входного наблюдения, имеющие как большие, так и меньшие значения аргументов, чем у оцениваемого сигнала.

Если в процессе обработки опираться только на данные двух лучей

, то будет получен двумерный каузальный фильтр. При добавлении к ним третьего луча

реализуется полукаузальная фильтрация. Используя лучи

, можем осуществить одномерную некаузальную фильтрацию. Коррекция, которой необходимо в этих случаях подвергнуть формулу (3.47), вполне очевидна.

Соотношение (3.47) дает возможность выполнить двумерную обработку изображения в виде некоторой совокупности одномерных процедур. Весь цикл вычислений можно представить следующим образом. Выполняется обработка всех строк изображения в прямом направлении (слева направо), в результате чего в каждой точке образуется распределение

. При этом используются одномерные рекуррентные процедуры, описанные выше. Далее происходит повторное сканирование строк, но в “обратном времени” - справа налево, в процессе которого вычисляются распределения

. Затем изображение аналогично дважды обрабатывается по столбцам - сверху вниз и снизу вверх, в результате чего определяются частные АРВ

. Вычислением одноточечного АРВ

завершается первый этап обработки. На втором этапе происходит объединение всех частных АРВ в каждой точке кадра в окончательное АРВ, а также на его основе вычисляются точечные оценки изображения

.

С точки зрения скорости вычислений данная технология обработки является очень привлекательной. Следует, вместе с тем, иметь в виду, что для ее реализации необходим достаточный запас оперативной памяти, чтобы хранить промежуточные результаты обработки, к числу которых относятся все частные АРВ. В этом отношении вычислительный процесс может быть существенно оптимизирован, поскольку ни одно из частных АРВ не представляет окончательной ценности. Это позволяет, например, не хранить отдельно пять различных распределений, входящих в правую часть (3.47), а по мере получения очередного сомножителя формировать произведение, именно которое и следует хранить в памяти до завершения вычислений. Очевидно, что структура вычислений, как и в одномерном случае, удобна для реализации при помощи многоканального вычислительного устройства.

Структура распределений очень сильно влияет на требуемые объем вычислений и ресурс памяти. Имеются очень “удобные” в этом смысле виды распределений. Например, если для описания изображения применима модель случайного поля с гауссовским распределением, то для представления каждого из частных и финального АРВ в (3.47) требуется наличие всего двух параметров - математического ожидания и дисперсии. Именно это и определяет конкретный характер и количество вычислений в процессе фильтрации, а также объем необходимой памяти.

Другим примером такого рода может служить математическая модель бинарного случайного поля, которое в различных точках принимает значения

или

. Такое описание также является очень экономичным, поскольку АРВ содержит всего две вероятности

, непосредственное вычисление которых и выполняется при помощи (3.47).

Существует отдельный вопрос, связанный с применимостью марковских двумерных моделей (3.45), (3.46), позволяющих построить эффективные двухэтапные процедуры. Его изучение является достаточно непростой теоретической задачей. В частности, в работах [3.6.,3.8] установлено, что и для гауссовских, и для бинарных случайных полей необходимым и достаточным условием применимости (3.45) является возможность представления двумерных корреляционных функций этих полей в разделимом виде, т.е. в виде произведения двух множителей, один из которых описывает корреляцию изображения по строке, а второй - по столбцу. Дополнительные требования, вытекающие из (3.46), сводятся к существованию марковских свойств у одномерных последовательностей в горизонтальном и вертикальном сечениях изображения. В двух указанных примерах наличие таких свойств связано с экспоненциальным видом корреляционных функций этих одномерных сечений изображения.

На рис. 3.9 приведены результаты экспериментальной проверки двумерных двухэтапных алгоритмов фильтрации изображения. На рис. 3.9.а показано тестовое бинарное изображение “острова”, на рис. 3.9.б - изображение, искаженное белым гауссовским шумом (отношение сигнал/шум

дБ).

Рис.3.9. в иллюстрирует применение простой поэлементной пороговой обработки (рис. 1.4.а), при которой порог определялся так, чтобы реализовывалась одноточечная процедура максимума апостериорной вероятности. На рис. 3.9.г, 3.9.д и 3.9.е показаны различные результаты двухэтапной фильтрации. Первый из них соответствует одномерной каузальной фильтрации, второй - также одномерной, но некаузальной, а третий - двумерной некаузальной процедуре. Визуальное сравнение результатов говорит об очень низком качестве поэлементной обработки. При ее использовании вероятность


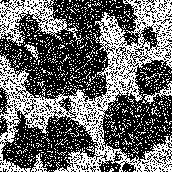а)	б)	в)

г)	д)	е)
Рис. 3.9. Двухэтапная марковская фильтрация изображения

ошибки (т.е. события, состоящего в замене числа

числом

или наоборот) составила 0.23. Качество обработки улучшается при использовании фильтрации, причем оно повышается как при переходе от одномерной каузальной (при которой вероятность ошибки составляет 0.086) к одномерной некаузальной (вероятность ошибки 0.041), так и при переходе к двумерной обработке, при которой достигается вероятность ошибки равная 0.022. Таким образом, применение одномерной некаузальной фильтрации позволяет уменьшить вероятность ошибки в 5 раз по сравнению с поэлементной пороговой обработкой, а двумерной некаузальной фильтрации - почти в 10 раз. Эти примеры говорят об очень высокой эффективности, которой может достигать фильтрация, и убеждают в полезности тех значительных усилий, которые необходимы для нахождения эффективных алгоритмов.

3.6. Медианная фильтрация

Все линейные алгоритмы фильтрации приводят к сглаживанию резких перепадов яркости изображений, прошедших обработку. Этот недостаток, особенно существенный, если потребителем информации является человек, принципиально не может быть исключен в рамках линейной обработки. Дело в том, что линейные процедуры являются оптимальными при гауссовском распределении сигналов, помех и наблюдаемых данных. Реальные изображения, строго говоря, не подчиняются данному распределению вероятностей.

Причем, одна из основных причин этого состоит в наличии у изображений разнообразных границ, перепадов яркости, переходов от одной текстуры к другой и т. п.. Поддаваясь локальному гауссовскому описанию в пределах ограниченных участков, многие реальные изображения в этой связи плохо представляются как глобально гауссовские объекты. Именно это и служит причиной плохой передачи границ при линейной фильтрации.

Вторая особенность линейной фильтрации - ее оптимальность, как только что упоминалось, при гауссовском характере помех. Обычно этому условию отвечают шумовые помехи на изображениях, поэтому при их подавлении линейные алгоритмы имеют высокие показатели. Однако, часто приходится иметь дело с изображениями, искаженными помехами других типов. Одной из них является импульсная помеха. При ее воздействии на изображении наблюдаются белые или (и) черные точки, хаотически разбросанные по кадру. Применение линейной фильтрации в этом случае неэффективно - каждый из входных импульсов ( по сути - дельта-функция) дает отклик в виде импульсной характеристики фильтра, а их совокупность способствует распространению помехи на всю площадь кадра.

Удачным решением перечисленных проблем является применение медианной фильтрации, предложенной Дж. Тьюки в 1971 г. для анализа экономических процессов. Наиболее полное исследование медианной фильтрации применительно к обработке изображений представлено в сборнике [3.9]. Отметим, что медианная фильтрация представляет собой эвристический метод обработки, ее алгоритм не является математическим решением строго сформулированной задачи. Поэтому исследователями уделяется большое внимание анализу

эффективности обработки изображений на ее основе и сопоставлению с другими методами.

При применении медианного фильтра (МФ) происходит последовательная обработка каждой точки кадра, в результате чего образуется последовательность оценок. В идейном отношении обработка в различных точках независима (этим МФ похож на масочный фильтр), но в целях ее ускорения целесообразно алгоритмически на каждом шаге использовать ранее выполненные вычисления.

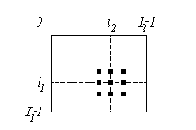
При медианной фильтрации используется двумерное окно (апертура фильтра), обычно имеющее центральную симметрию, при этом его центр располагается в текущей точке фильтрации. На рис. 3.10 показаны два примера наиболее часто применяемых вариантов окон в виде креста и в виде квадрата. Размеры апертуры принадлежат к числу параметров, оптимизируемых в процессе анализа эффективности алгоритма. Отсчеты изображения, оказавшиеся в пределах окна, образуют рабочую выборку текущего шага.


а)	б)
Рис. 3.10. Примеры окон при медианной фильтрации

Двумерный характер окна позволяет выполнять, по существу, двумерную фильтрацию, поскольку для образования оценки привлекаются данные как из текущих строки и столбца, так и из соседних. Обозначим рабочую выборку в виде одномерного массива

; число его элементов равняется размеру окна, а их расположение произвольно. Обычно применяют окна с нечетным числом точек

(это автоматически обеспечивается при центральной симметрии апертуры и при вхождении самой центральной точки в ее состав). Если упорядочить последовательность

по возрастанию, то ее медианой будет тот элемент выборки, который занимает центральное положение в этой упорядоченной последовательности. Полученное таким образом число и является продуктом фильтрации для текущей точки кадра. Понятно, что результат такой обработки в самом деле не зависит от того, в какой последовательности представлены элементы изображения в рабочей выборке

. Введем формальное обозначение описанной процедуры в виде:

. (3.48)

Рассмотрим пример. Предположим, что выборка имеет вид:

, а элемент 250, расположенный в ее центре, соответствует текущей точке фильтрации

(рис. 3.10). Большое значение яркости в этой точке кадра может быть результатом воздействия импульсной (точечной) помехи. Упорядоченная по возрастанию выборка имеет при этом вид

{45,55,75,99,104,110,136,158,250}, следовательно, в соответствии с процедурой (3.48), получаем

.

Видим, что влияние “соседей” на результат фильтрации в текущей точке привело к “игнорированию” импульсного выброса яркости, что следует рассматривать как эффект фильтрации. Если импульсная помеха не является точечной, а покрывает некоторую локальную область, то она также может быть подавлена. Это произойдет, если размер этой локальной области будет меньше, чем половина размера апертуры МФ. Поэтому для подавления импульсных помех, поражающих локальные участки изображения, следует увеличивать размеры апертуры МФ.

Из (3.48) следует, что действие МФ состоит в “игнорировании” экстремальных значений входной выборки - как положительных, так и отрицательных выбросов. Такой принцип подавления помехи может быть применен и для ослабления шума на изображении. Однако исследование подавления шума при помощи медианной фильтрации показывает, что ее эффективность при решении этой задачи ниже, чем у линейной фильтрации [3.9].

Результаты экспериментов, иллюстрирующие работу МФ, приведены на рис. 3.11. В экспериментах применялся МФ, имеющий квадратную апертуру со

стороной равной 3. В левом ряду представлены изображения, искаженные помехой, в правом - результаты их медианной фильтрации. На рис. 3.11.а и рис. 3.11.в показано исходное изображение, искаженное импульсной помехой. При ее наложении использовался датчик случайных чисел с равномерным на интервале [0, 1] законом распределения, вырабатывающий во всех точках кадра независимые случайные числа. Интенсивность помехи задавалась вероятностью

ее возникновения в каждой точке. Если для случайного числа

, сформированного в точке

, выполнялось условие

, то яркость изображения

в этой точке замещалась числом 255, соответствующим максимальной яркости (уровню белого). На рис. 3.11.а действием импульсной помехи искажено 5 % (

=0.05), а на рис. 3.11.в - 10 % элементов изображения. Результаты обработки говорят о практически полном подавлении помехи в первом случае и о ее значительном ослаблении во втором.


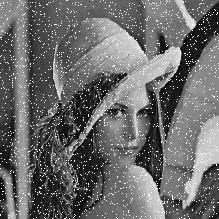а)	б)

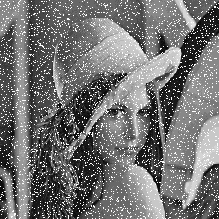в)	г)

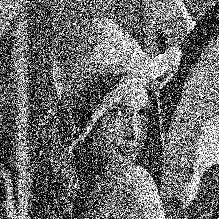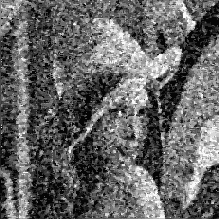д)	е)
Рис. 3.11. Примеры медианной фильтрации

<

Рис. 3.11. д показывает изображение, искаженное независимым гауссовским шумом при отношении сигнал/шум

дБ, а рис. 3.11.е - результат его фильтрации медианным фильтром. Условия данного эксперимента позволяют сравнивать его результаты с результатами рассмотренной выше линейной фильтрации. В таблице 3.1 приведены данные, дающие возможность такого сравнения. Для различных методов фильтрации в этой таблице приводятся значения относительного среднего квадрата ошибок

и коэффициента ослабления шума

для случая, когда отношение сигнал/шум на входе фильтра составляет -5 дБ.

	масочный фильтр с оптимальн. КИХ	масочный фильтр с равномерн. КИХ	двумерный рекуррентн. фильтр	двумерный фильтр Винера	медианный фильтр
	0.309	0.395	0.29	0.186	0.539
	10.2	8.0	10.9	17.0	5.86
Табл.3.1. Сравнение эффективности подавления шума при фильтрации изображений, дБ

Наибольшей эффективностью обладает двумерный фильтр Винера, уменьшающий средний квадрат ошибок в 17 раз. Медианный фильтр имеет наименьшую из всех рассмотренных фильтров эффективность, ему соответствует

=5.86. Тем не менее, это число свидетельствует о том, что и при его помощи удается значительно снизить уровень шума на изображении.

Вместе с тем, как говорилось выше, и что демонстрирует рис. 3.11.е, медианная фильтрация в меньшей степени сглаживает границы изображения, чем любая линейная фильтрация. Механизм этого явления очень прост и заключается в следующем. Предположим, что апертура фильтра находится вблизи границы, разделяющей светлый и темный участки изображения, при этом ее центр располагается в области темного участка. Тогда, вероятнее всего, рабочая выборка будет содержать большее количество элементов с малыми значениями яркости, и, следовательно, медиана будет находиться среди тех элементов рабочей выборки, которые соответствуют этой области изображения. Ситуация меняется на противоположную, если центр апертуры смещен в область более высокой яркости.

Содержание раздела