Восстановление изображений
Из-за несовершенства формирующих и регистрирующих систем записанное ими изображение представляет собой искаженную (нечеткую) копию оригинала. Основными причинами искажений, приводящих к ухудшению четкости, являются ограниченная разрешающая способность формирующей системы, расфокусировка, наличие искажающей среды (например, атмосферы), движение камеры по отношению к регистрируемому объектуи т.п. Устранение или ослабление искажений с целью повышения резкости относится к задаче восстановления изображений.
Наиболее общая схема формирования изображения представлена на рис. 4.1,

Рис.4.1. Схема формирования изображения

где






Вид оператора






4.1. Модели изображений и их линейных искажений
4.1.1. Формирование изображений
Большинство формирующих систем в первом приближении можно рассматривать как линейные и инвариантные к сдвигу. Изображения, сформированные такими системами, претерпевают линейные пространственно-инвариантные искажения,
характеризующиеся тем, что механизм их возникновения один и тот же для всех точек

С учетом вышеизложенного наблюдаемое нерезкое изображение

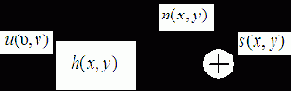
Рис.4.2. Линейная модель формирования изображения
а математическая модель процесса его формирования имеет вид:

где


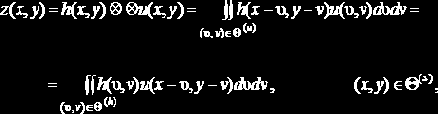
где





В выражении (4.1) учтено, что изображения, встречающиеся в практических задачах, имеют конечные размеры. Это означает, что яркость изображения полагается равной нулю всюду, кроме некоторой конечной области, которую будем называть кадром и обозначать через








Относительные размеры кадров изображений и ФРТ в модели формирования (4.1) имеют важное значение. Как будет показано ниже, конечность их размеров значительно усложняет решение задачи восстановления. Размеры кадров



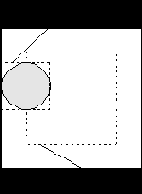
Рис.4.3. Относительные размеры изображения и ФРТ
Кадр










Поэтому даже если регистрируемый объект имеет бесконечные размеры наблюдаемое изображение формируется лишь только за счет некоторой его части. Причем размеры кадра наблюдаемого изображения всегда меньше или равны размерам исходного. Размеры кадров исходного и наблюдаемого изображений равны лишь при отсутствии линейных искажений, т.е. когда импульсная характеристика искажающей системы равна дельта-функции. Нас будет интересовать восстановление изображения в пределах кадра




Для изображений, представленных в цифровой форме, двумерные функции








где

Аргументы с индексом 1 обозначают номер строки, а с индексом 2 - номер столбца. В дискретном случае размеры кадра (число отсчетов)



Операция свертки, которая имеется в формулах (4.1) и (4.4), эквивалентна произведению в частотной области. Это позволяет выполнить быструю имитацию линейных искажений с помощью ДПФ, заменив обычную свертку циклической (смотри главу 3). Как правило, размеры кадра ФРТ много меньше размеров кадра исходного изображения, поэтому перед преобразованием массив

Спектр линейно-искаженного изображения





где








Рассмотрим импульсные и частотные характеристики формирующих систем при смазе и расфокусировке.
4.1.2. Размытие вследствие движения (смаз)
Смаз изображения возникает при взаимном движении камеры и объекта относительно друг друга во время экспозиции. Наблюдаемое изображение окажется как бы результатом наложения со смещением множества исходных изображений. Мы рассмотрим только тот случай, когда камера перемещается с постоянной горизонтальной скоростью относительно снимаемого объекта. ФРТ и передаточная функция такой системы определяются выражениями:


где длина смаза


где размеры кадра


 |
 |
|
Рис.4.4. Взаимное расположение изображения и ФРТ при смазе |
Рис.4.5. Изображние модуля частотной характеристики искажающей системы |

Изображение модуля



На рис.4.7 приведен искаженный вариант исходного изображения «Сатурн» (рис.4.6). Горизонтальный смаз составляет 15 элементов. Исходное изображение содержит


 |
 |
|
Рис.4.6.Исходное изображение “Сатурн” |
Рис.4.7. Смазанное изображение “Сатурн” |
Четкость изображения характеризуется воспроизведением мелких деталей и определяется разрешающей способностью формирующей системы. Разрешающая способность, например, оптической системы численно выражается количеством пар черно-белых линий на 1 мм изображения, которое формируется объективом системы. Если плоскость формируемого изображения находится в фокусе объектива, то пучок лучей, исходящий от точки на объекте, сходится в точку на изображении. При расфокусировке точка воспроизводится в виде некоторого пятна (кружка размытия), и две близко расположенные точки на исходном изображении сливаются в одну на наблюдаемом. Величина кружка размытия зависит от фокусного расстояния объектива, а также от расстояний от объектива до объекта и до плоскости формируемого изображения [4.1]. Дискретное изображение будет четким (сфокусированным), если диаметр кружка размытия не превышает шага дискретизации

При расфокусировке распределение интенсивности на изображении точечного источника, формируемого тонкой линзой с круговой апертурой, постоянно в пределах кружка размытия радиусом


Из (4.8) следует, что размеры кадра


где

В дискретном случае ФРТ (4.8) имеет вид:

На рис.4.8 и 4.9 показаны ФРТ для тонкой линзы (4.10) и модуль ее передаточной функции при радиусе кружка размытия


 |
 |
|
Рис.4.8. ФРТ тонкой линзы |
Рис.4.9. Изображение модуля частотной характеристики тонкой линзы |
Земную атмосферу также можно рассматривать как оптическую систему. В качестве приближенной модели ФРТ такой системы используется двумерный гауссовский импульс

который в дискретном случае имеет вид

где



Очевидно, что точки, для которых выполняется условие (4.2), образуют круг радиусом

Следовательно, чем больше


 |
 |
|
Рис.4.10. ФРТ атмосферы Земли |
Рис.4.11. Изображение модуля частотной характеристики атмосферы Земли |
 |
|
Рис.4.12. Дефокусированное изображение “Сатурн” |


Таким образом,
можно выделить три основных фактора, которые существенно усложняют решение проблемы восстановления изображений.
1. Искажения типа расфокусировка или смаз проявляются в ослаблении верхних пространственных частот изображения, т.к. формирующие системы представляют собой фильтры нижних частот. При этом отношение сигнал/шум на верхних частотах, определяющих четкость изображения, будет значительно хуже, чем для изображения в целом.
Если система, формирующая изображение, ослабляет сигнал на каких-то пространственных частотах, то при восстановлении он должен быть усилен в той мере, в какой был ослаблен. Вместе с сигналом будут усиливаться и шумы. Поэтому улучшение качества изображения по резкости может привести к ухудшению его качества по зашумленности.
2. Яркость на краях кадра искаженного изображения зависит от яркости объектов, расположенных вне кадра, за счет свертки исходного изображения с ФРТ. При восстановлении изображений из-за неполной информации о сигнале вне кадра возникают краевые эффекты. Влияние краевых эффектов на качество восстановления в ряде случаев оказывается даже более существенным, чем зашумленность изображения.
3. При искажениях, вызванных движением или расфокусировкой камеры, передаточные функции (4.7) и (4.9) имеют нули, наличие которых обусловлено осциллирующим характером передаточных функций. Поскольку спектр искаженного изображения равен произведению спектра исходного изображения и передаточной функции (см. (4.5)), то наличие нулей приводит к полной утрате данных об исходном изображении на соответствующих частотах. По этой причине не удается абсолютно точно восстановить исходное изображение по наблюдаемому изображению, даже если отсутствуют шумы наблюдения и размеры кадров неограничены.
При решении задач восстановления изображений используются различные алгоритмы, как имеющие строгое математическое обоснование, так и эмпирические. Для искажений, описываемых уравнением свертки, эти алгоритмы условно можно разделить на три основные группы: алгоритмы решения системы алгебраических уравнений, алгоритмы фильтрации изображений в частотной области и итерационные алгоритмы.
4.2. Алгебраические методы восстановления изображений
Соотношение (4.4) для цифровых изображений фактически представляет собой систему линейных алгебраических уравнений относительно



Удобно представить соотношения (4.3) и (4.4) в матричной форме, используя лексикографическое упорядочивание. Для этого двумерный массив наблюдаемого изображения
















где искаженное изображение

Символ





Если шумами наблюдения можно пренебречь, то задача восстановления изображения сводится к нахождению оценки (решения)


Если бы



Однако матричное уравнение (4.16) представляет собой недоопределенную
систему линейных алгебраических уравнений, т.к. количество неизвестных





Среди всех возможных решений недоопределенной разрешимой системы (4.16) в качестве оценки


где



где

Точное восстановление исходного изображения при отсутствии шумов возможно, во-первых, когда искаженное изображение получено в результате циклической свертки исходного изображения и ФРТ. Во-вторых, когда объекты исходного изображения расположены в центре кадра и наблюдаются на фоне постоянной яркости, причем расстояние от объектов до границ кадра больше апертуры ФРТ. В том и другом случаях число неизвестных будет равно числу уравнений, т.к. объекты, расположенные вне кадра, не будут влиять на яркость наблюдаемого изображения. Иными словами, точное восстановление при отсутствии шума возможно тогда, когда ограничение размеров кадра наблюдаемого изображения не приводит к потере информации об исходном изображении.
Для искаженных изображений, наблюдаемых в присутствии шумов, к элементам вектора-столбца



В этом случае оптимальным оператором (в смысле критерия наименьших квадратов (4.21)), формирующим оценку



Таким образом, в обоих рассмотренных случаях обобщенное обращение матриц дает оптимальное решение, удовлетворяющее критериям наименьших квадратов (4.19) или (4.21).
Следует подчеркнуть, что, несмотря на одинаковые названия, по сути это два разных критерия. Для разрешимой недоопределенной системы (4.16)) (когда выбирается одно решение из множества возможных) ошибка


Основным недостатком алгебраических алгоритмов восстановления изображений является необходимость выполнения трудоемких операций обращения, умножения и транспонирования матриц огромных размеров. Напомним, что размер матрицы

4.3. Методы восстановления изображений на основе
пространственной фильтрации
Методы восстановления изображений, которые будут рассмотрены в данном разделе, реализуются с помощью ДПФ в частотной области. При этом обычная свертка заменяется циклической как в модели формирования искаженного изображения (4.4), так и в процедуре восстановления методом пространственной фильтрации. Все изображения





При циклической свертке модель (4.4) формирования искаженного изображения определяется соотношением

где

Применяя к (4.22) ДПФ, получим

Система восстановления изображений на основе пространственной фильтрации представляет собой линейный пространственно-инвариантный двумерный фильтр. На выходе этого фильтра формируется оценка

исходного изображения


4.3.1. Инверсный фильтр
Простейшим способом восстановления четкости изображения является обработка наблюдаемого изображения в пространственно-частотной области инверсным фильтром [4.5]. Передаточная функция инверсного восстанавливающего фильтра определяется соотношением


Она выбирается из условия


Таким образом, восстановленное изображение равно сумме исходного изображения и шума наблюдения, прошедшего через инверсный фильтр. При отсутствии шума достигается точное восстановление инверсным фильтром исходного изображения


На рис. 4.13. и 4.14 приведены результаты восстановления изображений «Часы» и «Сатурн» инверсным фильтром: а) исходные изображения размером



Восстановить изображение «Часы» инверсным фильтром не удается из- за краевых эффектов. Практически идеальное восстановление изображения «Сатурн» объясняется тем, что объекты наблюдаются на фоне постоянной яркости и расположены в центре кадра. В этом случае изображения


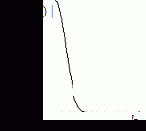
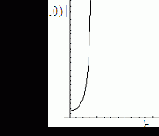
На рис. 4.15 и 4.16 приведены сечения типичных частотных характеристик ФРТ и соответствующих им инверсных фильтров, из которых следует, что модуль передаточной функции формирующей системы, как правило, стремится к нулю на высоких частотах. Кроме того, нули в передаточной функции имеются в рабочей полосе частот при расфокусировке камеры (4.10) и смазе (4.6). В этом случае инверсный фильтр является сингулярным, т.к. модуль его передаточной функции становится бесконечно большим на пространственных частотах, соответствующих нулевым значениям модуля передаточной функции искажающей системы. Причем наличие даже относительно слабого шума приводит к появлению интенсивных шумовых составляющих на выходе инверсного фильтра, полностью разрушающих изображение. Этот факт иллюстрируется рис.4.17. К дефокусированному изображению «Сатурн» (рис. 4.14.б) был добавлен аддитивный дельта-коррелированный шум. Из восстановленного изображения видно, что даже при пренебрежимо малом уровне шума (отношение сигнал/шум

 |
 |
|
а) |
б) |
 |
|
|
в) |
|
|
Рис.4.13. Результаты восстанвления изображения “Часы” |
 |
 |
|
а) |
б) |
 |
|
|
в) |
|
|
Рис.4.14. Результаты восстанвления изображения “Сатурн” |
 |
 |
||
 |
 |
||
|
Рис.4.15. Частотные характеристики искажающей системы с цилиндрической ФРТ и инверсного фильтра |
Рис.4.16. Частотные характеристики искажающей системы с гауссовской ФРТ и инверсного фильтра |
||
 |
|||
Рис.4.17. Результат восстановления изображения “Сатурн” при  |
|||
Существуют частные методы ослабления шумов, которые заключаются в ограничении полосы инверсного фильтра. Последовательно с инверсным фильтром включается корректирующее звено, модуль передаточной функции которого стремится к нулю за пределами некоторой наперед заданной граничной частоты. При этом граничная частота выбирается из компромисса между снижением уровня шума и четкостью восстановленного изображения. Однако эти методы не решают проблем краевых эффектов и наличия нулей передаточной функции формирующей системы в рабочем диапазоне частот.
Таким образом, несмотря на очевидную простоту метода инверсной фильтрации, он может успешно использоваться для восстановления ограниченного класса изображений, у которых уровень фона на краях постоянен. Кроме того, метод инверсной фильтрации обладает чрезвычайно низкой помехоустойчивостью.
4.3.2. Фильтр Винера
Инверсная фильтрация обладает низкой помехоустойчивостью, потому что этот метод не учитывает зашумленность наблюдаемого изображения. Значительно менее подвержен влиянию помех и сингулярностей, обусловленных нулями передаточной функции искажающей системы, фильтр Винера (смотри главу 3), т.к. при его синтезе наряду с видом ФРТ используется информация о спектральных плотностях мощности изображения и шума. При этом полагается, что изображение является реализацией случайного двумерного поля. Частотная характеристика восстанавливающего фильтра Винера, полученная для периодически продолженных изображений, с учетом (2.34) имеет вид [4.6]

где





Преобразуем передаточную функцию фильтра Винера (4.28) следующим образом:

Анализируя соотношения (4.28) и (4.29), можно отметить следующее:
1. При отсутствии шума фильтр Винера переходит в инверсный фильтр. Следовательно, в области низких частот, где, как правило, отношение сигнал/шум велико, передаточные функции инверсного и винеровского фильтров практически совпадают.
2. При уменьшении спектральной плотности мощности исходного изображения передаточная функция фильтра Винера стремится к нулю. Для изображений это характерно на верхних частотах.
3. На частотах, соответствующих нулям передаточной функции формирующей системы, передаточная функция фильтра Винера также равна нулю. Таким образом решается проблема сингулярности восстанавливающего фильтра.
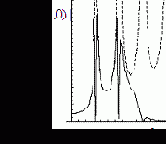
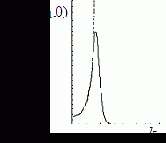
На рис. 4.18 приведены одномерные сечения типичных передаточных функций винеровских фильтров (сплошная линия). Здесь же для сравнения приведены сечения передаточных функций инверсных фильтров (4.15) и (4.16), которые обозначены штриховой линией.
 |
 |
|
Рис.4.18. Частотный характеристики фильтра Винера при цилиндрической и гауссовской ФРТ |





 |
 |
|
а) |
б) |
Рис.4.19. Восстановление дефокусированного изображения “Сатурн” при  |
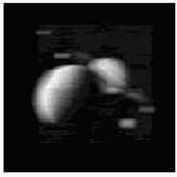 |
 |
|
а) |
б) |
Рис.4.20. Восстановление смазанного изображения “Сатурн” при  |

Осциллирующая помеха на результатах восстановления изображения «Часы» (рис. 4.21.б и рис.4.22.в) вызвана краевыми эффектами. Очевидно, что ее уровень существенно меньше, чем при инверсной фильтрации (см. рис.4.13.в). Однако винеровский фильтр лишь частично компенсирует краевые эффекты, которые делают качество восстановления неудовлетворительным.
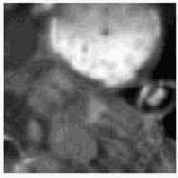 |
 |
|
а) |
б) |
Рис.4.21. Восстановление дефокусированного изображения “Часы” при  |
|
 |
 |
|
а) |
б) |
 |
|
|
в) |
|
Рис.4.22. Восстановление смазанного изображения “Часы” при  |
4.3.3. Компенсация краевых эффектов при
восстановлении линейно-искаженных изображений
На восстановленных изображениях, приведенных на рис.4.13.в, 4.21.б и 4.22.в, присутствует осциллирующая помеха большой интенсивности, которая возникает из-за того, что инверсный фильтр и фильтр Винера были синтезированы без учета ограниченных размеров наблюдаемых изображений. Вследствие того, что искаженное изображение записывается в кадре конечного размера, в усеченном изображении происходит потеря информации, содержащейся в исходном изображении вблизи границ. Поэтому при коррекции линейных искажений усеченного изображения возникают ложные детали в виде ряби или полос, интенсивность которых особенно велика при цилиндрической форме ФРТ и равномерном смазе.
К сожалению, решить уравнение Винера-Хопфа для сигналов и изображений, наблюдаемых на ограниченном интервале, не удается. Поэтому отсутствуют оптимальные пространственно-инвариантные фильтры, учитывающие краевые эффекты. Для компенсации краевых эффектов используются различные эвристические алгоритмы.
Некоторые из них будут рассмотрены в данном подразделе.
Если нас интересует центральная часть изображения и его размеры значительно больше размеров кадра ФРТ, то для компенсации краевых эффектов применяют умножение наблюдаемого изображения на функцию окна


При дефокусировке функция окна является разделимой относительно пространственных координат:


Хорошие результаты дает функция окна [4.8]

форма которой определяется двумя независимыми параметрами




На рис 4.23 и 4.24 приведены результаты восстановления изображения «Часы» при горизонтальном смазе, где а - результаты умножения строк искаженного изображения, приведенного на рис.4.22.б, на окно Кайзера и окно (4.30); б - результаты восстановления фильтром Винера. Параметры окон подбирались, исходя из визуального качества восстанавливаемых изображений.
Уровень яркости на краях изображений, умноженных на окно, стремится к нулю, поэтому вместе с уменьшением краевых эффектов сужаются границы восстанавливаемого изображения. Кроме того, оптимальные параметры окон зависят от параметров искажающей системы и определяются опытным путем, что затрудняет практическое применение алгоритмов восстановления.
Учесть ограниченные размеры наблюдаемого изображения можно на этапе синтеза фильтра Винера, который использует информацию о спектрально-корреляционных характеристиках изображения. Получение изображения ограниченных размеров эквивалентно умножению бесконечного изображения на окно единичной яркости, размеры которого равны размерам кадра

Очевидно, что спектрально- корреляционные характеристики такого усеченного изображения будут отличаться от аналогичных характеристик бесконечных изображений. Корреляционная функция усеченного изображения может быть получена путем умножения на окно
 |
 |
|
а) |
б) |
|
Рис. 4.23. Восстановление с использованием окна Кайзера |
|
 |
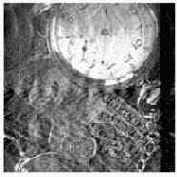 |
|
а) |
б) |
|
Рис. 4.24. Восстановление с использованием окна (4.30) |

корреляционной функции неограниченного изображения [4.9]. В этом случае спектральная плотность мощности усеченного изображения равна свертке спектральной плотности мощности неограниченного изображения и спектральной плотности окна (4.31). Подставляя соответствующие спектральные плотности мощности в уравнение Винера-Хинчина и решая его, получим коэффициент передачи фильтра для усеченного изображения [4.10]

где

На рис. 4.25 приведен результат восстановления изображения «Часы» фильтром (4.32), откуда следует, что фильтр (4.32) практически полностью компенсирует краевые эффекты. Это позволяет отказаться от предварительной обработки. Качество восстановления изображения в центре и на краях почти одинаковое. Параметры фильтра (4.32) полностью определяются исходными данными и не требуют дополнительной подстройки. При использовании быстрого преобразования Фурье для обработки изображений объем вычислений при реализации фильтра (4.32) такой же, как и для фильтра Винера (4.28).
 |
|
Рис.4.25. Результат восстановления с компенсацией краевых эффектов |




Простейшей является процедура одномерной экстраполяции. Яркость изображения вдоль строк и столбцов за пределами кадра наблюдаемого изображения


Коэффициенты




 |
 |
|
а) |
б) |
|
Рис. 4.26. Восстановление с применением экстраполяции |
Улучшить качество восстановления можно, используя одновременно экстраполяцию наблюдаемого изображения и фильтра (4.32). Результат такой комбинированной процедуры приведен на рис 4.27. Рассмотренные методы восстановления являются линейными. Их широкое использование обусловлено достаточно простыми методами синтеза и анализа линейных систем, а также высокой вычислительной эффективностью. Однако эти методы не являются оптимальными и не всегда обеспечивают эффективную компенсацию искажений. Линейная обработка является лишь приближением к оптимальной обработке, т.к. статистические характеристики подавляющего большинства изображений являются негауссовскими.
Кроме того, линейные методы не учитывают априорные данные о восстанавливаемых изображениях. Поэтому интерес представляют нелинейные методы обработки изображений. Синтез оптимальных нелинейных алгоритмов, как правило, значительно сложнее, чем линейных. Однако существуют линейные методы восстановления, которые достаточно просто могут быть преобразованы в нелинейные, учитывающие априорные данные об изображениях и помехах. Ярким примером таких методов являются итерационные методы (методы последовательных приближений).
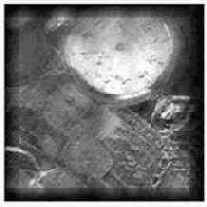
Рис.4.27. Восстановление с использованием экстраполяции и
компенсации краевых эффектов
4.4. Итерационные методы восстановления изображений
Итерационными методами называют способы решения задач, в которых, выбирая некоторое начальное приближенное решение, вычисляют следующие, более точные приближения, используя предыдущие.
Рассмотрим один из способов построения итерационных процедур, основанный на разложении в ряд частотной характеристики инверсного фильтра [4.6]. Спектр оценки исходного изображения при инверсной фильтрации определяется соотношением

Представим передаточную функцию инверсного фильтра


Подставляя (4.34) в (4.33), получим

Соотношение (4.35) позволяет представить процедуру нахождения оценки






где каждое последующее приближение вычисляется по предыдущему. Взяв преобразование Фурье от соотношений (4.36), получим итерационную процедуру Ван Циттера [4.11]:

(4.37)

которую можно интерпретировать как процедуру последовательного нахождения поправок




В итерационном алгоритме (4.37) нахождение обратного оператора заменяется на многократное вычисление свертки.
При использовании итерационных алгоритмов необходимо знать ответы на два вопроса - сходится ли он и, если сходится, то к какому решению. Сходимость алгоритма (4.37) к решению (4.33) определяется сходимостью ряда бесконечной геометрической прогрессии (4.34). Этот ряд сходится при


Условие (4.38) выполняется для гауссовской ФРТ. При цилиндрической ФРТ и равномерном смазе соотношение (4.33) заменяют на эквивалентное соотношение

Тогда итерационный алгоритм (4.37) имеет вид [4.6]

(4.39)

где




Очевидно, что рассмотренный итерационный алгоритм является линейным и не имеет никаких преимуществ по сравнению с линейными алгоритмами. Однако этот метод позволяет эффективно бороться с краевыми эффектами и чрезмерным усилением шумов при восстановлении изображений. Итеративный процесс всегда можно остановить, если шум и осциллирующая помеха на изображении резко усиливаются. Остановка итеративного процесса означает усечение ряда (4.34), что приводит к ограничению коэффициента усиления за пределами некоторой граничной частоты. С увеличением длины ряда возрастают граничная частота и коэффициент усиления фильтра. Этот эффект иллюстрируется рис. 4.28, где приведены одномерные сечения частотных характеристик фильтров при 10-ти и 15-ти слагаемых в ряде (4.34) (сплошные линии). Здесь же для сравнения приведено одномерное сечение частотной характеристики инверсного фильтра (штриховая линия).

Рис. 4.28. Частотные характеристики итерационного фильтра на разных шагах
На рис 4.29 приведены результаты восстановления изображения «Часы», где а и б - повторно приведенные исходное (рис.4.22.а) и искаженное в результате смаза (рис 4.22.б) изображения; в - восстановленное изображение итерационным алгоритмом (4.37) ( число итераций



 |
 |
|
а) |
б ) |
 |
 |
|
в) |
г) |
|
Рис. 4.29. Восстановление изображения “Часы” итерационным алгоритмом |





Наряду с описанными выше свойствами итерационные алгоритмы могут быть легко преобразованы в нелинейные путем введения нелинейных ограничений для восстанавливаемого изображения [4.6, 4.11]. Ограничения формулируются на основе априорных данных о форме или структуре объектов на исходном изображении. К априорным данным относятся такие свойства изображения, как неотрицательность яркости, ее верхний и нижний пределы, минимальная мощность сигнала, ограниченная пространственная и спектральная протяженность и. т.п.
Даже учет такого простейшего ограничения как верхний и нижний пределы значений яркости приводит к значительному улучшению качества восстановления, т.к. среди всех возможных решений выбирается то, которое не имеет сильных осциляций яркости.
Итерационный алгоритм, например (4.39), с ограничением имеет вид

(4.41)

где

Например, если используется оператор ограничения на неотрицательность


Нелинейный итерационный алгоритм (4.41) будет сходится, если сходится линейный алгоритм (4.39) и оператор



Для большинства цифровых изображений диапазон изменения яркости равен












 |
 |
|
а) |
б) |
 |
 |
|
в) |
г) |
 |
 |
|
д) |
е) |
|
Рис. 4.30.Восстановление изображения “Текст” нелинейным итерационным алгоритмом |
