Использование функции assert для проверки утверждений и ситуация отказ

В реализации стека на Си неоднократно использовалась функция assert, в переводе с английского "утверждение". Фактическим аргументом функции является логическое выражение. Если оно истинно, то ничего не происходит; если ложно, то программа завершается аварийно, выдавая диагностику ошибки.

Функция assert является реализацией конструкции "утверждение", использование которой преследует две цели:

программист в процессе написания программы может явно сформулировать утверждение, которое, по его мнению, должно выполняться в данной точке программы. В этом случае конструкция "утверждение" выполняет роль комментария, облегчая создание и понимание программы; компьютер при выполнении программы проверяет все явно сформулированные утверждения. Истинность утверждения соответствует предположениям программиста, сделанным в процессе написания программы, поэтому выполнение программы продолжается. Ложность утверждения свидетельствует об ошибке программиста. При этом выдается сообщение об ошибке и выполнение программы немедленно прекращается. Таким образом, конструкция "утверждение " позволяет компьютеру проверять корректность программы непосредственно в процессе ее выполнения.

Ситуация, когда программа аварийно завершается из-за того, что утверждение не выполняется, называется отказом.

Многие предписания структуры данных выполнимы не во всех ситуациях. Например, элемент можно взять из стека только в случае, когда стек не пуст. Поэтому перед началом выполнения предписания "Взять элемент" проверяется условие "стек не пуст":

double st_pop() { // Взять элемент: вещ assert(sp >= 0); // утв: стек не пуст . . .

Если это утверждение ложно, то возникает ситуация "отказ ": компьютер завершает работу, выдавая диагностику ошибки. Невыполнение утверждения всегда свидетельствует об ошибке программиста: программа должна быть написана таким образом, чтобы некорректные исходные данные не приводили к отказу.

Использование конструкции "утверждение " — мощное средство отладки программы.
Важность ситуации "отказ " была осознана в процессе эволюции программирования далеко не сразу. На заре развития программирования на первом плане были требования эффективности программы — ее компактности и быстродействия. И лишь по мере проникновения компьютеров во все области жизни на первый план выступила надежность программы. В современном мире от надежности программы во многих случаях зависит человеческая жизнь, поэтому любые способы повышения надежности очень важны.

Почему в случае невыполнения утверждения возникает ситуация "отказ"? Альтернативой могло бы быть игнорирование некорректной ситуации и то или иное продолжение программы: например, при попытке извлечения элемента из пустого стека выдавался бы ноль. На самом деле это худшее решение из всех, которые только можно придумать! Любую ошибку надо диагностировать и исправлять как можно раньше, а имитация полезной деятельности в некорректной ситуации крайне опасна. Это может привести, например, к тому, что программа, управляющая посадкой самолетов, будет успешно сажать в среднем 999 самолетов из 1000, а каждый тысячный будет разбиваться.

Практическая рекомендация: используйте конструкцию "утверждение" как можно чаще. Если при разработке программы вы считаете, что в данной точке должно выполняться некоторое утверждение, сформулируйте его явно, чтобы компьютер при выполнении программы мог бы его проверить. Таким способом находится и исправляется львиная доля ошибок.

При частом использовании конструкции "утверждение" возникает проблема с уменьшением скорости выполнения программы. Она решена в языках Си и C++ следующим образом: на самом деле конструкция assert в Си — это не функция, а макроопределение, которое обрабатывается препроцессором. Текст Си-программы может транслироваться в двух режимах: отладочном и нормальном. В нормальном режиме в соответствии со стандартом ANSI определена переменная NDEBUG препроцессора. Для определения макрокоманды assert используется условная трансляция: если переменная NDEBUG определена, то assert определяется как пустое выражение; если нет, то assert определяется как проверка условия и вызов функции _assert (к имени добавлен символ подчеркивания) в случае, когда условие ложно.Функция _assert печатает диагностику ошибки и завершает выполнение программы, т.е. реализует ситуацию "отказ".

Таким образом, условие реально проверяется лишь при трансляции программы в отладочном режиме. Благодаря этому быстродействие программы не снижается, однако, в нормальном режиме условие не проверяется. Примерно как при обучении плаванию: в бассейне человек надевает спасательный круг, но снимает его, когда начинает плавать в океане.

Использование стека в программировании

Стек применяется довольно часто, причем в самых разных ситуациях. Объединяет их следующая цель: нужно сохранить некоторую работу, которая еще не выполнена до конца, при необходимости переключения на другую задачу. Стек используется для временного сохранения состояния не выполненного до конца задания. После сохранения состояния компьютер переключается на другую задачу. По окончании ее выполнения состояние отложенного задания восстанавливается из стека, и копьютер продолжает прерванную работу.

Почему именно стек используется для сохранения состояния прерванного задания? Предположим, что компьютер выполняет задачу A. В процессе ее выполнения возникает необходимость выполнить задачу B. Состояние задачи A запоминается, и компьютер переходит к выполнению задачи B. Но ведь и при выполнении задачи B компьютер может переключиться на другую задачу C, и нужно будет сохранить состояние задачи B, прежде чем перейти к C. Позже, по окончании C будет сперва восстановлено состояние задачи B, затем, по окончании B, — состояние задачи A. Таким образом, восстановление происходит в порядке, обратном сохранению, что соответствует дисциплине работы стека.

Стек позволяет организовать рекурсию, т.е. обращение подпрограммы к самой себе либо непосредственно, либо через цепочку других вызовов. Пусть, например, подпрограмма A выполняет алгоритм, зависящий от входного параметра X и, возможно, от состояния глобальных данных. Для самых простых значений X алгоритм реализуется непосредственно. В случае более сложных значений X алгоритм реализуется как сведение к применению того же алгоритма для более простых значений X. При этом подпрограмма A обращается сама к себе, передавая в качестве параметра более простое значение X. При таком обращении предыдущее значение параметра X, а также все локальные переменные подпрограммы A сохраняются в стеке. Далее создается новый набор локальных переменных и переменная, содержащая новое (более простое) значение параметра X. Вызванная подпрограмма A работает с новым набором переменных, не разрушая предыдущего набора.
По окончании вызова старый набор локальных переменных и старое состояние входного параметра X восстанавливаются из стека, и подпрограмма продолжает работу с того места, где она была прервана.

На самом деле даже не приходится специальным образом сохранять значения локальных переменных подпрограммы в стеке. Дело в том, что локальные переменные подпрограммы (т.е. ее внутренние, рабочие переменные, которые создаются в начале ее выполнения и уничтожаются в конце) размещаются в стеке, реализованном аппаратно на базе обычной оперативной памяти. В самом начале работы подпрограмма захватывает место в стеке под свои локальные переменные, этот участок памяти в аппаратном стеке называют обычно блок локальных переменных или по-английски frame ( "кадр "). В момент окончания работы подпрограмма освобождает память, удаляя из стека блок своих локальных переменных.

Кроме локальных переменных, в аппаратном стеке сохраняются адреса возврата при вызовах подпрограмм. Пусть в некоторой точке программы A вызывается подпрограмма B. Перед вызовом подпрограммы B адрес инструкции, следующей за инструкцией вызова B, сохраняется в стеке. Это так называемый адрес возврата в программу A. По окончании работы подпрограмма B извлекает из стека адрес возврата в программу A и возвращает управление по этому адресу. Таким образом, компьютер продолжает выполнение программы A, начиная с инструкции, следующей за инструкцией вызова. В большинстве процессоров имеются специальные команды, поддерживающие вызов подпрограммы с предварительным помещением адреса возврата в стек и возврат из подпрограммы по адресу, извлекаемому из стека. Обычно команда вызова назывется call, команда возврата — return.

В стек помещаются также параметры подпрограммы или функции перед ее вызовом. Порядок их помещения в стек зависит от соглашений, принятых в языках высокого уровня. Так, в языке Си или C++ на вершине стека лежит первый аргумент функции, под ним второй и так далее. В Паскале все наоборот, на вершине стека лежит последний аргумент функции. (Поэтому, кстати, в Си возможны функции с переменным числом аргументов, такие, как printf, а в Паскале нет.)



В Фортране-4, одном из самых старых и самых удачных языков программирования, аргументы передаются через специальную область памяти, которая может располагаться не в стеке, поскольку до конца 70-х годов XX века еще существовали компьютеры вроде IBM 360 или ЕС ЭВМ без аппаратной реализации стека. Адреса возврата также сохранялись не в стеке, а в фиксированных для каждой подпрограммы ячейках памяти. Программисты называют такую память статической в том смысле, что статические переменные занимают всегда одно и то же место в памяти в любой момент работы программы. При использовании только статической памяти рекурсия невозможна, поскольку при новом вызове предыдущие значения локальных переменных разрушаются. В эталонном Фортране-4 использовались только статические переменные, а рекурсия была запрещена. До сих пор язык Фортран широко используется в научных и инженерных расчетах, однако, современный стандарт Фортрана-90 уже вводит стековую память, устраняя недостатки ранних версий языка.

Язык PostScript

Другой яркий пример использования обратной польской записи — это графический язык PostScript. Он предназначен для печати текстов высокого качества на лазерных принтерах; он является стандартом представления текстов типографского качества, не зависящим от конкретной модели принтера.

То, что PostScript — язык программирования, для многих людей, знакомых с типографским делом, но далеких от программирования, звучит непривычно. Общепринятое мнение, что компьютер работает с числами и в основном что-то вычисляет, не вполне верно. Не менее часто компьютерная программа работает с текстами и с изображениями. Текст, содержащийся в обычном текстовом файле, можно рассматривать с двух точек зрения. Можно трактовать его просто как текст статьи или книги. Рассмотрим, однако, процесс печати текста на обычном (не графическом) принтере. Принтер соединен с компьютером кабелем, и компьютер просто посылает через этот кабель один за другим символы, составляющие текст. В этом случае букву A, входящую в текст, следует рассматривать как команду, предписывающую принтеру напечатать символ A в текущей точке страницы, используя текущий шрифт. После этого координату x текущей точки надо увеличить на ширину буквы A. С этой точки зрения весь текст можно трактовать как программу его собственной печати. В случае обычного текстового файла эта программа весьма примитивна, в ней, к примеру, нет команд смены шрифтов, изменения текущей позиции, рисования линий и т.д. Понятно, что текст типографского качества не может быть представлен обычным текстовым файлом.

В случае использования языка PostScript файл, пересылаемый на PostScript-принтер, представляет собой программу печати текста. Язык PostScript имеет огромное количество возможностей, и вряд ли найдется много людей, владеющих им. Чаще всего PostScript-программа создается другой программой обработки текста. Например, PostScript-файл создается TEX-ом для печати на принтере. (TEX — это язык записи текстов, содержащих математические формулы, созданный замечательным математиком и теоретиком программирования Дональдом Кнутом. Фактически TEX представляет собой язык программирования. Данная книга подготовлена в TEX'е с использованием макропакета LaTEX 2?.) Текстовые процессоры, такие, как Adobe Acrobat или MS Word, также в случае печати на профессиональном PostScript-принтере преобразуют текст в PostScript-программу. (Более точно, такое преобразование осуществляется драйверами операционной системы.) PostScript-файлы очень удобны для распространения: поскольку это файлы в обычном текстовом формате, они будут напечатаны одинаково в любой стране независимо от национальных кодировок, операционных систем, наличия шрифтов и т.п.

PostScript-программа представляет собой обратную польскую запись в том смысле, что всякая команда записывается после своих аргументов. При выполнении PostScript-программы используется стек. Рассмотрим для примера несложную программу, рисующую график функции y = sin(x). Вот какая картинка рисуется в результате выполнения этой программы:

(Подчеркнем особо, что все рисунки, содержащиеся в данном пособии, реализованы в виде PostScript-программ, написанных вручную без использования каких-либо графических редакторов.)

Ниже приведен полный текст PostScript-программы, рисующей график функции. Отметим сразу, что символ процента % используется в языке PostScript в качестве комментария:

% Файл "func.ps" % Рисование графика функции y = f(x)

% Перейти от пунктов (1/72 дюйма) к миллиметрам 2.83 2.83 scale

0.2 setlinewidth % Установить толщину линии

% Нарисовать координатную ось X: 1 15 moveto % переместиться в точку (1, 15) 60 15 lineto % провести линию к точке (60, 15) % Рисуем стрелку: 57 16 moveto % переместиться в точку (57, 16) 60 15 lineto % провести линию к точке (60, 15) 57 14 lineto % провести линию к точке (57, 14) stroke % нарисовать построенные линии

% Нарисовать координатную ось Y: 30 1 moveto % переместиться в точку (30, 1) 30 30 lineto % провести линию к точке (30, 30) % Рисуем стрелку: 29 27 moveto % переместиться в точку (29, 27) 30 30 lineto % провести линию к точке (30, 30) 31 27 lineto % провести линию к точке (31, 27) stroke % нарисовать построенные линии

% Определение функции % f(x) = 5 * sin((x - 30) * 0.2 * 180/Pi) + 15 % Дано: число x на вершине стека. % Надо: заменить вершину стека на f(x). /Func { 30 sub 0.2 mul 57.296 mul sin 5 mul 15 add } def

% Рисуем график функции

0.3 setlinewidth % установить толщину линии 2 2 Func moveto % переместиться в точку (2, f(2)) 2.5 0.5 58 { % цикл для x от 2.5 до 58 шаг 0.5 dup % удвоить вершину стека Func % заменить x в вершине стека на f(x) lineto % провести линию к точке (x, f(x)) } for % конец цикла stroke % нарисовать построенные линии

/Times-Roman findfont % загрузить шрифт Times-Roman 4 scalefont % установить размер шрифта 4 мм setfont % установить текущий шрифт

40 23 moveto % переместиться в точку (40, 23) (y = sin x) show % напечатать текст "y = sin x"

% Надписи на осях координат 59 11 moveto % переместиться в точку (59, 11) (x) show % напечатать текст "x"

26 28 moveto % переместиться в точку (26, 28) (y) show % напечатать текст "y"

showpage % напечатать страницу

Разберем подробно некоторые элементы этой программы. В первой выполняемой строке устанавливается миллиметровая шкала:

2.83 2.83 scale

По умолчанию в языке PostScript единицей измерения является один пункт, или 1/72 дюйма. Всякий программист помнит, что один дюйм равен 2.54 миллиметра. Вычислим отношение одного миллиметра к одному пункту:

1 mm / 1 pt = 1 mm / (1/72)" = = 1 mm / (2.54/72) mm = 2.834645

Таким образом, увеличивая масштаб в 2.83 раза, мы переходим от пунктов к миллиметрам. Для изменения масштаба мы помещаем в стек два числа 2.83, соответствующих изменению масштабов по x и y. Затем выполняется команда scale (изменить масштаб). Со стека при этом снимаются два числа, и масштабы по x и по y изменяются.

Разные команды могут иметь различное число аргументов. Например, вторая строка устанавливает толщину линии.

0.2 setlinewidth

Команда setlinewidth имеет один аргумент, который помещается на стек перед ее вызовом. При выполнении команды он снимается со стека, и толщина линии устанавливается равной числу, снятому со стека.

Третья строка перемещает текущую позицию в точку с координатами x = 1, y = 15.

1 15 moveto % переместиться в точку (1, 15)

(В качестве единиц используются миллиметры, начало координат находится в левом нижнем углу страницы.) В стек сначала добавляются два числа, соответствующие координатам x и y, и затем выполняется команда moveto, которая снимает два числа со стека и перемещает курсор в точку, координаты которой были получены из стека.

Большинство строк программы понятны благодаря комментариям, которые в языке PostScript можно записывать в конце любой строки после символа %. Отметим две конструкции, которые использованы в программе. Фрагмент

/Func { 30 sub 0.2 mul 57.296 mul sin 5 mul 15 add } def

определяет функцию с именем Func. Функцию затем можно вызвать, просто записав ее имя, как это делается, например, в строке

Func % заменить x в вершине стека на f(x)

Вызов функции в PostScript'е эквивалентен записи тела функции в точке вызова. Параметры и результат функции передаются через стек.

Тело функции при ее определении записывается внутри фигурных скобок. В данном случае это строка

30 sub 0.2 mul 57.296 mul sin 5 mul 15 add

Функция вызывается при условии, что ее аргумент x находится на вершине стека. В результате выполнения тела функции вершина стека заменяется на выражение

5 * sin((x - 30) * 0:2 * 57:296) + 15

Здесь используются масштабирующие множители, чтобы график выглядел красиво на печати. Так, масштаб по обеим осям равен 5 мм, поэтому мы умножаем значение sin на 5, а аргумент sin на 0.2, т.е. на 1/5. Центр графика смещается в точку с координатами (30,15), поэтому мы прибавляем к значению sin число 15, а от аргумента вычитаем 30. Наконец, аргумент функции sin в языке PostScript задается в градусах. Чтобы перейти от радианов к градусам, мы умножаем агрумент в радианах на множитель 57.296 = 180/

. Сравните выражения:

5 * sin((x - 30) * 0:2 * 57:296) + 15 x 30 sub 0.2 mul 57.296 mul sin 5 mul 15 add

Первое представляет собой обычную запись формулы, второе — обратную польскую запись.

Фрагмент

2.5 0.5 58 { % цикл для x от 2.5 до 58 шаг 0.5 dup % удвоить вершину стека Func % заменить x в вершине стека на f(x) lineto % провести линию к точке (x, f(x)) } for % конец цикла

представляет собой арифметический цикл. На вершину стека последовательно помещается число x в диапазоне от 2.5 до 58 с шагом 0.5. Для каждого значения выполняется тело цикла, заключенное в фигурные скобки. В теле цикла вершина стека сначала удваивается командой dup, после ее выполнения в вершине стека будут лежать два одинаковых значения x, x. Затем вызывается функция Func, которая заменяет значение x в вершине стека на y, где y равно значению функции. Затем проводится линия от предыдущей точки к точке (x,y). При этом команда lineto удаляет оба значения x, y из стека.

Язык PostScript является достаточно мощным языком программирования, в нем есть переменные, функции, циклы, условный оператор и т.п. Используемая в нем обратная польская запись очень удобна для выполнения на компьютере. Поэтому интерпретатор языка PostScript легко встраивается в конструкцию принтера (который, конечно же, всегда содержит более или менее сложный компьютер внутри себя) и не сильно увеличивает стоимость принтера.

Язык Java, байткод которого также представляет собой обратную польскую запись, был тоже первоначально разработан для программирования недорогих бытовых приборов. Стековый вычислитель устроен просто и может быть применен там, где быстродействие не играет особой роли, зато важна скорость и дешевизна разработки программы и аппаратуры.

Массив как базовая структура

Оперативная память с точки зрения программиста — это массив элементов. Любой элемент массива можно прочитать или записать сразу, за одно элементарное действие. Массив можно рассматривать как простейшую структуру данных. Структуры данных, в которых возможен непосредственный доступ к произвольным их элементам, называют структурами данных с прямым, или с произвольным доступом (по-английски random access). Наряду с массивом, структурой данных с прямым доступом является множество, которое будет рассмотрено ниже. В других структурах данных непосредственный доступ возможен лишь к одному или нескольким элементам, для доступа к остальным элементам надо выполнить дополнительные действия. Такие структуры данных называются структурами последовательного доступа. Примером структуры последовательного доступа является магнитофон, на которым записаны песни. В любой момент можно прослушать лишь очередную песню. Чтобы добраться до других музыкальных фрагментов, надо перемотать ленту вперед или назад. Кстати, такие магнитофоны, или накопители на магнитной ленте, очень долго использовались на ЭВМ, хотя сейчас уступили свое место более надежным и компактным системам (съемным магнитным и оптическим дискам, флэш-памяти и т.п.). Устройство компьютерного магнитофона было аналогично устройству обычного бытового магнитофона.

С логической точки зрения, массивом является также важнейшая составляющая компьютера — магнитный диск. Элементарной единицей чтения и записи для магнитного диска служит блок. Размер блока зависит от конструкции конкретного диска, обычно он кратен 512. За одну элементарную операцию можно прочесть или записать один блок с заданным адресом.

Итак, наиболее важные запоминающие устройства компьютера — оперативная память и магнитный диск — представляют собой массивы. Массив как бы дан программисту свыше, так же как математику целые числа. Работа с элементами массива осуществляется исключительно быстро, все элементы массива доступны без всяких предварительных действий.

Тем не менее массивов недостаточно для написания эффективных программ.
Например, поиск элемента в массиве, если его элементы не упорядочены, невозможно реализовать эффективно: нельзя изобрести ничего лучшего, кроме последовательного перебора элементов. В случае упорядоченного хранения элементов можно использовать эффективный бинарный поиск, но затруднения возникают при добавлении или удалении элементов в середине массива и приводят к массовым операциям, т.е. операциям, время выполнения которых зависит от числа элементов структуры. От этих недостатков удается избавиться, реализуя множество элементов на базе сбалансированных деревьев или хеш-функции.

Есть и другие причины, по которым необходимо использовать более сложные, чем массивы, структуры данных. Логика многих задач требует организации определенного порядка доступа к данным. Например, в случае очереди элементы можно добавлять только в конец, а забирать только из начала очереди; в стеке доступны лишь элементы в вершине стека, в списке — элементы до и за указателем.

Наконец, массив имеет ограниченный размер. Увеличение размера массива в случае необходимости приводит к переписыванию его содержимого в захваченную область памяти большего размера, т.е. опять же к массовой операции. От этого недостатка свободны ссылочные реализации структур данных: реализации на основе линейных списков или на основе деревьев.

Общее понятие структуры данных

Структура данных — это исполнитель, который организует работу с данными, включая их хранение, добавление и удаление, модификацию, поиск и т.д. Структура данных поддерживает определенный порядок доступа к ним. Структуру данных можно рассматривать как своего рода склад или библиотеку. При описании структуры данных нужно перечислить набор действий, которые возможны для нее, и четко описать результат каждого действия. Будем называть такие действия предписаниями. С программной точки зрения, системе предписаний структуры данных соответствует набор функций, которые работают над общими переменными.

Структуры данных удобнее всего реализовывать в объектно-ориентированных языках. В них структуре данных соответствует класс, сами данные хранятся в переменных-членах класса (или доступ к данным осуществляется через переменные-члены), системе предписаний соответствует набор методов класса. Как правило, в объектно-ориентированных языках структуры данных реализуются в виде библиотеки стандартных классов: это так называемые контейнерные классы языка C++, входящие в стандартную библиотеку классов STL, или классы, реализующие различные структуры данных из библиотеки Java Developer Kit языка Java.

Тем не менее, структуры данных столь же успешно можно реализовывать и в традиционных языках программирования, таких как Фортран или Си. При этом следует придерживаться объектно-ориентированного стиля программирования: четко выделить набор функций, которые осуществляют работу со структурой данных, и ограничить доступ к данным только этим набором функций. Сами данные реализуются как статические (не глобальные) переменные. При программировании на языке Си структуре данных соответствуют два файла с исходными текстами:

заголовочный, или h-файл, который описывает интерфейс структуры данных, т.е. набор прототипов функций, соответствующий системе предписаний структуры данных;файл реализации, или Си-файл, в котором определяются статические переменные, осуществляющие хранение и доступ к данным, а также реализуются функции, соответствующие системе предписаний структуры данных

Структура данных обычно реализуется на основе более простой базовой структуры, ранее уже реализованной, или на основе массива и набора простых переменных. Следует четко различать описание структуры данных с логической точки зрения и описание ее реализации. Различных реализаций может быть много, с логической же точки зрения (т.е. с точки зрения внешнего пользователя) все они эквивалентны и различаются, возможно, лишь скоростью выполнения предписаний.

Очередь

Очередь как структура данных понятна даже людям, не знакомым с программированием. Очередь содержит элементы, как бы выстроенные друг за другом в цепочку. У очереди есть начало и конец. Добавлять новые элементы можно только в конец очереди, забирать элементы можно только из начала. В отличие от обычной очереди, которую всегда можно при желании покинуть, из середины программистской очереди удалять элементы нельзя.

Очередь можно представить в виде трубки. В один конец трубки можно добавлять шарики — элементы очереди, из другого конца они извлекаются. Элементы в середине очереди, т.е. шарики внутри трубки, недоступны. Конец трубки, в который добавляются шарики, соответствует концу очереди, конец, из которого они извлекаются — началу очереди. Таким образом, концы трубки не симметричны, шарики внутри трубки движутся только в одном направлении.

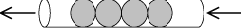
В принципе, можно было бы разрешить добавлять элементы в оба конца очереди и забирать их также из обоих концов. Такая структура данных в программировании тоже существует, ее название — "дек", от англ. Double Ended Queue, т.е. очередь с двумя концами. Дек применяется значительно реже, чем очередь.

Использование очереди в программировании почти соответствует ее роли в обычной жизни. Очередь практически всегда связана с обслуживанием запросов, в тех случаях, когда они не могут быть выполнены мгновенно. Очередь поддерживает также порядок обслуживания запросов. Рассмотрим, к примеру, что происходит, когда человек нажимает клавишу на клавиатуре компьютера. Тем самым человек просит компьютер выполнить некоторое действие. Например, если он просто печатает текст, то действие должно состоять в добавлении к тесту одного символа и может сопровождаться перерисовкой области экрана, прокруткой окна, переформатированием абзаца и т.п.

Любая, даже самая простая, операционная система всегда в той или иной степени многозадачна. Это значит, что в момент нажатия клавиши операционная система может быть занята какой-либо другой работой. Тем не менее, операционная система ни в какой ситуации не имеет права проигноровать нажатие на клавишу.
Поэтому происходит прерывание работы компьютера, он запоминает свое состояние и переключается на обработку нажатия на клавишу. Такая обработка должна быть очень короткой, чтобы не нарушить выполнение других задач. Команда, отдаваемая нажатием на клавишу, просто добавляется в конец очереди запросов, ждущих своего выполнения. После этого прерывание заканчивается, компьютер восстанавливает свое состояние и продолжает работу, которая была прервана нажатием на клавишу. Запрос, поставленный в очередь, будет выполнен не сразу, а только когда наступит его черед.

В системе Windows работа оконных приложений основана на сообщениях, которые посылаются этим приложениям. Например, бывают сообщения о нажатии на клавишу мыши, о закрытии окна, о необходимости перерисовки области окна, о выборе пункта меню и т.п. Каждая программа имеет очередь запросов. Когда программа получает свой квант времени на выполнение, она выбирает очередной запрос из начала очереди и выполняет его. Таким образом, работа оконного приложения состоит, упрощенно говоря, в последовательном выполнении запросов из ее очереди. Очередь поддерживается операционной системой.

Подход к программированию, состоящий не в прямом вызове процедур, а в посылке сообщений, которые ставятся в очередь запросов, имеет много преимуществ и является одной из черт объектно-ориентированного программирования. Так, например, если оконной программе необходимо завершить работу по какой-либо причине, лучше не вызывать сразу команду завершения, которая опасна, потому что нарушает логику работы и может привести к потере данных. Вместо этого программа посылает самой себе сообщение о необходимости завершения работы, которое будет поставлено в очередь запросов и выполнено после запросов, поступивших ранее.

Простейшие структуры данных. Стек. Очередь

Наиболее важными из простейших структур данных являются стек и очередь. Эти структуры встречаются в программировании буквально на каждом шагу, в самых разнообразных ситуациях. Особенно интересен стек, который имеет самые неожиданные применения. В свое время при разработке серии ЭВМ IBM 360 в начале 70-х годов XX века фирма IBM совершила драматическую ошибку, не предусмотрев аппаратную реализацию стека. Эта серия содержала много других неудачных решений, но, к сожалению, была скопирована в Советском Союзе под названием ЕС ЭВМ (Единая Серия), а все собственные разработки были приостановлены. Это отбросило советскую промышленность на много лет назад в области разработки копьютеров.

Реализация очереди на базе массива

Как уже было сказано, программисту массив дан свыше, все остальные структуры данных нужно реализовывать на его основе. Конечно, такая реализация может быть многоэтапной, и не всегда массив выступает в качестве непосредственной базы реализации. В случае очереди наиболее популярны две реализации: непрерывная на базе массива, которую называют также реализацией на базе кольцевого буфера, и ссылочная реализация, или реализация на базе списка. Ссылочные реализации будут рассмотрены ниже.

При непрерывной реализации очереди в качестве базы выступает массив фиксированной длины N, таким образом, очередь ограничена и не может содержать более N элементов. Индексы элементов массива изменяются в пределах от 0 до N - 1. Кроме массива, реализация очереди хранит три простые переменные: индекс начала очереди, индекс конца очереди, число элементов очереди. Элементы очереди содержатся в отрезке массива от индекса начала до индекса конца.

При добавлении нового элемента в конец очереди индекс конца сперва увеличивается на единицу, затем новый элемент записывается в ячейку массива с этим индексом. Аналогично, при извлечении элемента из начала очереди содержимое ячейки массива с индексом начала очереди запоминается в качестве результата операции, затем индекс начала очереди увеличивается на единицу. Как индекс начала очереди, так и индекс конца при работе двигаются слева направо. Что поисходит, когда индекс конца очереди достигает конца массива, т.е. N - 1?

Ключевая идея реализации очереди состоит в том, что массив мысленно как бы зацикливается в кольцо. Считается, что за последним элементом массива следует его первый элемент (напомним, что последний элемент имеет индекс N - 1, а первый — индекс 0). При сдвиге индекса конца очереди вправо в случае, когда он указывает на последний элемент массива, он переходит на первый элемент. Таким образом, непрерывный отрезок массива, занимаемый элементами очереди, может переходить через конец массива на его начало.

Реализация одних структур на базе других

Реализация структуры данных на основе базовой структуры — это описание ее работы в терминах базовой структуры. При этом считается, что базовая структура либо дана изначально, либо уже кем-то реализована. Реализация должна включать в себя описание идеи реализации (каким образом элементы реализуемой структуры хранятся в базовой структуре, какие дополнительные переменные используются) и набор подпрограмм, каждая из которых моделирует некоторое предписание реализуемой структуры при помощи предписаний базовой структуры.

При рассмотрении любой структуры данных необходимо сначала описать ее с логической точки зрения, а затем рассмотреть различные способы ее реализации. В качестве базы реализации в большинстве случаев выступает либо массив, либо динамическая память (т.е. память, в которой можно захватывать участки требуемого размера и освобождать ранее захваченные участки, когда они уже больше не нужны; см. раздел 3.7.3).

Реализация стека на базе массива

Реализация стека на базе массива является классикой программирования. Иногда даже само понятие стека не вполне корректно отождествляется с этой реализацией.

Базой реализации является массив размера N, таким образом, реализуется стек ограниченного размера, максимальная глубина которого не может превышать N. Индексы ячеек массива изменяются от 0 до N - 1. Элементы стека хранятся в массиве следующим образом: элемент на дне стека располагается в начале массива, т.е. в ячейке с индексом 0. Элемент, расположенный над самым нижним элементом стека, хранится в ячейке с индексом 1, и так далее. Вершина стека хранится где-то в середине массива. Индекс элемента на вершине стека хранится в специальной переменной, которую обычно называют указателем стека (по-английски Stack Pointer или просто SP).

Когда стек пуст, указатель стека содержит значение минус единица. При добавлении элемента указатель стека сначала увеличивается на единицу, затем в ячейку массива с индексом, содержащимся в указателе стека, записывается добавляемый элемент. При извлечении элемента из стека сперва содержимое ячейки массива с индексом, содержащимся в указателе стека, запоминается во временной переменной в качестве результата операции, затем указатель стека уменьшается на единицу.

В приведенной реализации стек растет в сторону увеличения индексов ячеек массива. Часто используется другой вариант реализации стека на базе вектора, когда дно стека помещается в последнюю ячейку массива, т.е. в ячейку с индексом N - 1. Элементы стека занимают непрерывный отрезок массива, начиная с ячейки, индекс которой хранится в указателе стека, и заканчивая последней ячейкой массива. В этом варианте стек растет в сторону уменьшения индексов. Если стек пуст, то указатель стека содержит значение N (которое на единицу больше, чем индекс последней ячейки массива).

Реализация стека на языке Си

Реализуем стек вещественных чисел. Ниже мы используем эту реализацию как составную часть проекта Стековый калькулятор (см. раздел 4.4.2).

Реализация включает два файла: "streal.h", в котором описывается интерфейс исполнителя "Стек", и "streal.cpp", реализующий функции работы со стеком. Слово real обозначает вещественное число.

Используется первый вариант реализации стека на базе массива, описанный в предыдущем разделе: стек растет в сторону увеличения индексов массива. Пространство под массив элементов стека захватывается в динамической памяти в момент инициализации стека. Функции инициализации st_init передается размер массива, т.е. максимально возможное число элементов в стеке. Для завершения работы стека нужно вызвать функцию st_terminate, которая освобождает захваченную в st_init память. Ниже приведено содержимое файла "streal.h", описывающего интерфейс стека.

// Файл "streal.h" // Стек вещественных чисел, интерфейс // #ifndef ST_REAL_H #define ST_REAL_H

// Прототипы функций, реализующих предписания стека:

void st_init(int maxSize); // Начать работу (вх: цел // макс. размер стека) void st_terminate(); // Закончить работу void st_push(double x); // Добавить эл-т (вх: вещ x) double st_pop(); // Взять элемент: вещ double st_top(); // Вершина стека: вещ int st_size(); // Текущий размер стека: цел bool st_empty(); // Стек пуст? : лог int st_maxSize(); // Макс. размер стека: цел bool st_freeSpace(); // Есть свободное место? : лог void st_clear(); // Удалить все элементы double st_elementAt(int i); // Элемент стека на // глубине (вх: i): вещ #endif // Конец файла "streal.h"

Отметим, что директивы условной трансляции

#ifndef ST_REAL_H #define ST_REAL_H . . . #endif

используются для предотвращения повторного включения h-файла: при первом включении файла определяется переменная препроцессора ST_REAL_H, а директива "#ifndef ST_REAL_H" подключает текст, только если эта переменная не определена. Такой трюк используется практически во всех h-файлах.
Нужен он потому, что одни h-файлы могут подключать другие, и без этого механизма избежать повторного включения одного и того же файла трудно.

Файл "streal.cpp" описывает общие статические переменные, над которыми работают функции, соответствующие предписаниям стека, и реализует эти функции.

// Файл "streal.cpp" // Стек вещественных чисел, реализация // #include <stdlib.h> #include <assert.h> #include "streal.h" // Подключить описания функций стека

// Общие переменные для функций, реализующих // предписания стека: static double *elements = 0; // Указатель на массив эл-тов // стека в дин. памяти static int max_size = 0; // Размер массива static int sp = (-1); // Индекс вершины стека

// Предписания стека:

void st_init(int maxSize) { // Начать работу (вх: // макс. размер стека) assert(elements == 0); max_size = maxSize; elements = (double *) malloc( max_size * sizeof(double) ); sp = (-1); }

void st_terminate() { // Закончить работу if (elements != 0) { free(elements); } }

void st_push(double x) { // Добавить эл-т (вх: вещ x) assert( // утв: elements != 0 && // стек начал работу и sp < max_size-1 // есть своб. место ); ++sp; elements[sp] = x; }

double st_pop() { // Взять элемент: вещ assert(sp >= 0); // утв: стек не пуст --sp; // элемент удаляется из стека return elements[sp + 1]; }

double st_top() { // Вершина стека: вещ assert(sp >= 0); // утв: стек не пуст return elements[sp]; }

int st_size() { // Текущий размер стека: цел return (sp + 1); }

bool st_empty() { // Стек пуст? : лог return (sp < 0); }

int st_maxSize() { // Макс. размер стека: цел return max_size; }

bool st_freeSpace() { // Есть своб. место? : лог return (sp < max_size - 1); }

void st_clear() { // Удалить все элементы sp = (-1); }

double st_elementAt(int i) { // Элемент стека на // глубине (вх: i): вещ assert( // утв: elements != 0 && // стек начал работу и 0 <= i && i < st_size() // 0 <= i < размер стека ); return elements[sp - i]; } // Конец файла "streal.cpp"

Реализация стекового калькулятора на Си

Рассмотрим небольшой проект, реализующий стековый калькулятор на Си. Такая программа весьма полезна, поскольку позволяет проводить вычисления, не прибегая к записи промежуточных результатов на бумаге.

Программа состоит из трех файлов: "streal.h", "streal.cpp" и "stcalc.cpp". Первые два файла реализуют стек вещественных чисел, эта реализация уже рассматривалась ранее. Файл "stcalc.cpp" реализует стековый калькулятор на базе стека. Для сборки программы следует объединить все три файла в один проект. Команды построения программы зависят от операционной системы и компилятора, например, в системе Unix с компилятором "gcc" программу можно собрать с помощью команды

g++ -o stcalc -lm stcalc.cpp streal.cpp

в результате которой создается файл "stcalc" с программой, готовой к выполнению.

Ниже приведено содержимое файла "stcalc.cpp". Функция main, описанная в этом файле, организует диалог с пользователем в режиме команда-ответ. Пользователь может ввести число с клавиатуры, это число просто добавляется в стек. При вводе одного из четырех знаков арифметических операций +, -, *, / программа извлекает из стека два числа, выполняет указанное арифметическое действие над ними и помещает результат обратно в стек. Значение результата отображается также на дисплее. Кроме арифметических операций, пользователь может ввести название одной из стандартных функций: sin, cos, exp, log (натуральный логарифм). При этом программа извлекает из стека аргумент функции, вычисляет значение функции и помещает его обратно в стек. При желании список стандартных функций и возможных операций можно расширить. Наконец, можно выполнять еще несколько команд:

popclear=showhelpquit

удалить вершину стека;

очистить стек;

напечатать вершину стека;

напечатать содержимое стека;

напечатать подсказку;

завершить работу программы.

Каждая команда стекового калькулятора реализуется с помощью отдельной функции. Например, вычитание реализуется с помощью функции onSub():

static void onSub() { double y, x; if (st_size() < 2) { printf("Stack depth < 2.\n"); return; } y = st_pop(); x = st_pop(); st_push(x - y); display(); }

В начале функции проверяется, что глубина стека не меньше двух. В противном случае, выдается сообщение об ошибке, и функция завершается. Далее из стека извлекаются операнды y и x операции вычитания. Элементы извлекаются из стека в порядке, обратном их помещению в стек, поэтому y извлекается раньше, чем x. Затем вычисляется разность y - x, ее значение помещается обратно в стек и печатается на дисплее, для печати вершины стека вызывается функция display.

Приведем полный текст программы.

// Файл "stcalc.cpp" // Реализация стекового калькулятора на базе стека // #include <stdio.h> #include <stdlib.h> #include <ctype.h> #include <string.h> #include <math.h> #include "streal.h" // Интерфейс исполнителя "стек"

// Прототипы функций, реализующих команды калькулятора: // Арифметические операции static void onAdd(); static void onSub(); static void onMul(); static void onDiv();

// Добавить число в стек(вх: текстовая запись числа) static void onPush(const char* line);

// Вычисление математических функций static void onSin(); // sin static void onCos(); // cos static void onExp(); // Экспонента static void onLog(); // Натуральный логарифм static void onSqrt(); // Квадратный корень

// Другие команды static void onPop(); // Удалить вершину стека static void onClear(); // Очистить стек static void display(); // Напечатать вершину стека static void onShow(); // Напечатать содержимое стека static void printHelp(); // Напечатать подсказку

int main() { char line[256]; // Буфер для ввода строки int linelen; // Длина строки

st_init(1024); // Стек.начать работу(1024) // 1024 — макс. глубина стека printHelp(); // Напечатать подсказку

while (true) { // Цикл до бесконечности scanf("%s", line); // ввести строку linelen = strlen(line); // длина строки if (linelen == 0) continue;



// Разобрать команду и вызвать реализующую // ее функцию if (strcmp(line, "+") == 0) { onAdd(); } else if (strcmp(line, "-") == 0) { onSub(); } else if (strcmp(line, "*") == 0) { onMul(); } else if (strcmp(line, "/") == 0) { onDiv(); } else if (strcmp(line, "sin") == 0) { onSin(); } else if (strcmp(line, "cos") == 0) { onCos(); } else if (strcmp(line, "exp") == 0) { onExp(); } else if (strcmp(line, "log") == 0) { onLog(); } else if (strcmp(line, "sqrt") == 0) { onSqrt(); } else if (strcmp(line, "=") == 0) { display(); } else if ( // Если это число isdigit(line[0]) || ( linelen > 1 && (line[0] == '-' || line[0] == '+') && isdigit(line[1]) ) ) { onPush(line); // Добавить число в стек } else if (strcmp(line, "pop") == 0) { onPop(); } else if (strcmp(line, "clear") == 0) { onClear(); } else if (strcmp(line, "show") == 0) { onShow(); } else if (strcmp(line, "quit") == 0) { break; // Завершить работу } else { // Неправильная команда => printHelp(); // напечатать подсказку } } return 0; }

static void onAdd() { double y, x; if (st_size() < 2) { printf("Stack depth < 2.\n"); return; } y = st_pop(); x = st_pop(); st_push(x + y); display(); }

static void onSub() { double y, x; if (st_size() < 2) { printf("Stack depth < 2.\n"); return; } y = st_pop(); x = st_pop(); st_push(x - y); display(); }

static void onMul() { double y, x; if (st_size() < 2) { printf("Stack depth < 2.\n"); return; } y = st_pop(); x = st_pop(); st_push(x * y); display(); }

static void onDiv() { double y, x; if (st_size() < 2) { printf("Stack depth < 2.\n"); return; } y = st_pop(); x = st_pop(); st_push(x / y); display(); }

static void onPush(const char* line) { double x = atof(line); st_push(x); }

static void onSin() { double x; if (st_empty()) { printf("Stack empty.\n"); return; } x = st_pop(); st_push(sin(x)); display(); }



static void onCos() { double x; if (st_empty()) { printf("Stack empty.\n"); return; } x = st_pop(); st_push(cos(x)); display(); }

static void onExp() { double x; if (st_empty()) { printf("Stack empty.\n"); return; } x = st_pop(); st_push(exp(x)); display(); }

static void onLog() { double x; if (st_empty()) { printf("Stack empty.\n"); return; } x = st_pop(); st_push(log(x)); display(); }

static void onSqrt() { double x; if (st_empty()) { printf("Stack empty.\n"); return; } if (st_top() < 0.0) { printf("Arg. of square root is negative.\n"); return; } x = st_pop(); st_push(sqrt(x)); display(); }

static void onPop() { st_pop(); }

static void onClear() { st_clear(); }

static void display() { if (!st_empty()) { printf("=%lf\n", st_top()); } else { printf("stack empty\n"); } }

static void onShow() { int d = st_size(); printf("Depth of stack = %d.", d); if (d > 0) printf(" Stack elements:\n"); else printf("\n");

for (int i = 0; i < d; i++) { printf(" %lf\n", st_elementAt(i)); } }

static void printHelp() { printf( "Stack Calculator commands:\n" " <number> Push а number in stack\n" " +, -, *, / Ariphmetic operations\n" " sin, cos, Calculate a function\n" " exp, log, \n" " sqrt \n" " = Display the stack top\n" " pop Remove the stack top\n" " show Show the stack\n" " clear Clear the stack\n" " quit Terminate the program\n" ); } // Конец файла "stcalc.cpp"

Пример работы программы "stcalc". Пусть нужно вычислить выражение (3*3 + 4*4)1/2

Запишем выражение, используя обратную польскую запись:

3, 3, *, 4, 4, *, +, sqrt

(через sqrt обозначается операция извлечения квадратного корня). Последовательно отдаем соответствующие команды стековому калькулятору. При работе программы stcalc получается следующий диалог:

Stack Calculator commands: <number> Push а number in stack +, -, *, / Ariphmetic operations sin, cos, Calculate a function exp, log, sqrt = Display the stack top pop Remove the stack top show Show the stack clear Clear the stack quit Terminate the program 3 3 * =9.000000 4 4 * =16.000000 + =25.000000 sqrt =5.000000



Обратная польская запись формул оказалась исключительно удобной при работе с компьютерами. Для вычислений используется стек, что позволяет работать с выражениями любой степени сложности. Реализация стекового вычислителя не представляет никакого труда. Имеется также простой алгоритм преобразования выражения из обычной записи, в которой знак операции указывается между аргументами, в ее обратную польскую запись. Все это привело к тому, что многие компиляторы языков высокого уровня используют обратную польскую запись в качестве внутренней формы представления программы. Рассмотрим, к примеру, язык программирования Java. Как всякий объектно-ориентированный язык, он является интерпретируемым, а не компилируемым языком. Это означает, что компилятор Java преобразует исходную Java-программу не в машинные коды, а в промежуточный язык, предназначенный для выполнения (интерпретации) на специальной Java-машине. В случае Java этот промежуточный язык называют байткодом. Компилятор Java помещает байткод в файл с расширением ".class". Байткод представляет собой, упрощенно говоря, обратную польскую запись Java-прогаммы, а Java-машина — стековый вычислитель.

Стек

Стек — самая популярная и, пожалуй, самая важная структура данных в программировании. Стек представляет собой запоминающее устройство, из которого элементы извлекаются в порядке, обратном их добавлению. Это как бы неправильная очередь, в которой первым обслуживают того, кто встал в нее последним. В программистской литературе общепринятыми являются аббревиатуры, обозначающие дисциплину работы очереди и стека. Дисциплина работы очереди обозначается FIFO, что означает первым пришел — первым уйдешь (First In First Out). Дисциплина работы стека обозначается LIFO, последним пришел — первым уйдешь (Last In First Out).

Стек можно представить в виде трубки с подпружиненым дном, расположеной вертикально. Верхний конец трубки открыт, в него можно добавлять, или, как говорят, заталкивать элементы. Общепринятые английские термины в этом плане очень красочны, операция добавления элемента в стек обозначается push, в переводе "затолкнуть, запихнуть". Новый добавляемый элемент проталкивает элементы, помещеные в стек ранее, на одну позицию вниз. При извлечении элементов из стека они как бы выталкиваются вверх, по-английски pop ("выстреливают").

Примером стека может служить стог сена, стопка бумаг на столе, стопка тарелок и т.п. Отсюда произошло название стека, что по-английски означает стопка. Тарелки снимаются со стопки в порядке, обратном их добавлению. Доступна только верхняя тарелка, т.е. тарелка на вершине стека. Хорошим примером будет также служить железнодорожный тупик, в который можно составлять вагоны.

Стековый калькулятор и обратная польская запись формулы

В 1920 г. польский математик Ян Лукашевич предложил способ записи арифметических формул, не использующий скобок. В привычной нам записи знак операции записывается между аргументами, например, сумма чисел 2 и 3 записывается как 2 + 3. Ян Лукашевич предложил две другие формы записи: префиксная форма, в которой знак операции записывается перед аргументами, и постфиксная форма, в которой знак операции записывается после аргументов. В префиксной форме сумма чисел 2 и 3 записывается как + 2 3, в постфиксной — как 2 3 +. В честь Яна Лукашевича эти формы записи называют прямой и обратной польской записью.

В польской записи скобки не нужны. Например, выражение

(2+3)*(15-7)

записывается в прямой польской записи как

* + 2 3 - 15 7,

в обратной польской записи — как

2 3 + 15 7 - *.

Если прямая польская запись не получила большого распространения, то обратная оказалась чрезвычайно полезной. Неформально преимущество обратной записи перед прямой польской записью или обычной записью можно объяснить тем, что гораздо удобнее выполнять некоторое действие, когда объекты, над которыми оно должно быть совершено, уже даны.

Обратная польская запись формулы позволяет вычислять выражение любой сложности, используя стек как запоминающее устройство для хранения промежуточных результатов. Такой стековый калькулятор был впервые выпущен фирмой Hewlett Packard. Обычные модели калькуляторов не позволяют вычислять сложные формулы без использования бумаги и ручки для записи промежуточных результатов. В некоторых моделях есть скобки с одним или двумя уровнями вложенности, но более сложные выражения вычислять невозможно. Также в обычных калькуляторах трудно понять, как результат и аргументы перемещаются в процессе ввода и вычисления между регистрами калькулятора. Калькулятор обычно имеет регистры X, Y и регистр памяти, промежуточные результаты каким-то образом перемещаются по регистрам, каким именно — запомнить невозможно.

В отличие от других калькуляторов, устройство стекового калькулятора вполне понятно и легко запоминается.
Калькулятор имеет память в виде стека. При вводе числа оно просто добавляется в стек. При нажатии на клавишу операции, например, на клавишу +, аргументы операции сначала извлекаются из стека, затем с ними выполняется операция, наконец, результат операции помещается обратно в стек. Таким образом, при выполнении операции с двумя аргументами, например, сложения, в стеке должно быть не менее двух чисел. Аргументы удаляются из стека и на их место кладется результат, то есть при выполнении сложения глубина стека уменьшается на единицу. Вершина стека всегда содержит результат последней операции и высвечивается на дисплее калькулятора.

Для вычисления выражения надо сначала преобразовать его в обратную польскую запись (при некотором навыке это легко сделать в уме). В приведенном выше примере выражение (2+3)*(15-7) преобразуется к

2 3 + 15 7 - *

Затем обратная польская запись просматривается последовательно слева направо. Если мы видим число, то просто вводим его в калькулятор, т.е. добавляем его в стек. Если мы видим знак операции, то нажимаем соответствующую клавишу калькулятора, выполняя таким образом операцию с числами на вершине стека.

Изобразим последовательные состояния стека калькулятора при вычислении по приведенной формуле. Сканируем слева направо ее обратную польскую запись:

2 3 + 15 7 - *

Стек вначале пуст. Последовательно добавляем числа 2 и 3 в стек.

| | вводим число 2

| 2 | вводим число 3 | 3 | | 2 |

Далее читаем символ + и нажимаем на клавишу + калькулятора. Числа 2 и 3 извлекаются из стека, складываются, и результат помещается обратно в стек.

| 3 | выполняем сложение | 5 | | 2 |

Далее, в стек добавляются числа 15 и 7.

| 5 | вводим число 15 | 15 | вводим число 7 | 7 | | 5 | | 15 | | 5 |

Читаем символ - и нажимаем на клавишу - калькулятора. Со стека при этом снимаются два верхних числа 7 и 15 и выполняется операция вычитания. Причем уменьшаемым является то число, которое было введено раньше, а вычитаемым — число, введенное позже. Иначе говоря, при выполнении некоммутативных операций, таких как вычитание или деление, правым аргументом является число на вершине стека, левым — число, находящееся под вершиной стека.

| 7 | выполняем вычитание | 8 | | 15 | | 5 | | 5 |

Наконец, читаем символ * и нажимаем на клавишу * калькулятора. Калькулятор выполняет умножение, со стека снимаются два числа, перемножаются, результат помещается обратно в стек.

| 8 | выполняем умножение | 40 | | 5 |

Число 40 является результатом вычисления выражения. Оно находится на вершине стека и высвечивается на дисплее стекового калькулятора.

Структуры данных

"Алгоритмы + структуры данных = программы". Это - название книги Никлауса Вирта, знаменитого швейцарского специалиста по программированию, автора языков Паскаль, Модула-2, Оберон. С именем Вирта связано развитие структурного подхода к программированию. Н.Вирт известен также как блестящий педагог и автор классических учебников.

Обе составляющие программы, выделенные Н.Виртом, в равной степени важны. Не только несовершенный алгоритм, но и неудачная организация работы с данными может привести к замедлению работы программы в десятки, а иногда и в миллионы раз. С другой стороны, владение теорией прораммирования и умение систематически применять ее на практике позволяет быстро разрабатывать эффективные и в то же время эстетически красивые программы.

AVL-деревья

Так называемые AVL-деревья (названные в честь их двух изобретателей Г.М. Адельсона-Вельского и Е.М. Ландиса) хранят дополнительно в каждой вершине разность между высотами левого и правого поддеревьев, которая в сбалансированном дереве может принимать только три значения: -1, 0, 1. Строго говоря, AVL-деревья не являются сбалансированными в смысле приведенного выше определения. Требуется только, чтобы для любой вершины AVL-дерева разность высот ее левого и правого поддеревьев была по абсолютной величине не больше единицы. При этом длины путей от корня к внешним вершинам могут различаться больше, чем на единицу. Можно, тем не менее, доказать, что и в случае AVL-деревьев их высота оценивается сверху логарифмически в зависимости от числа вершин:

h <= C log2 n

где константа C = 1.5. Обычно константы не очень важны в практическом программировании — принципиально лишь, по какому закону увеличивается время работы алгоритма при увеличении n. В данном случае зависимость логарифмическая, т.е. наилучшая из всех возможных (поскольку поиск невозможен быстрее чем за log2 n операций).

Новый элемент всегда добавляется в дерево в соответствии с упорядоченностью как левый или правый сын некоторой вершины, у которой данного сына до этого не было (или, как мы считаем, сын являлся внешним). Новая вершина добавляется как терминальная. После этого выполняется процедура восстановления балансировки. В ней используются следующие элементарные преобразования дерева, сохраняющие упорядоченность вершин:

вращение вершины x поддерева влево:

Здесь вершина x поддерева, которая является его корнем, опускается вниз и влево. Бывший правый сын d вершины x становится новым корнем поддерева, а x становится левым сыном d. (Вершины x и d, начальник и подчиненный, как бы меняются ролями: бывший начальник становится подчиненным.) Поддерево c, которое было левым сыном вершины d, переходит в подчинение от вершины d к вершине x и становится ее правым сыном. Отметим, что упорядоченность вершин сохраняется: a < b < c< d < e.
Таким образом, для выполнения преобразования надо лишь заменить фиксированное количество указателей в вершинах x, d, c и, возможно, в родительской для x вершине;

вращение вершины x поддерева вправо:

Здесь вершина x опускается вниз и вправо, ее бывший левый сын b становится новым корнем поддерева, а x — его правым сыном. Поддерево c переходит в подчинение от b к x.



Операции вращения носят локальный характер и позволяют при необходимости исправить баланс поддерева с корнем x. Например, для восстановления баланса дерева, показанного на следующем рисунке, достаточно выполнить одно вращение вершины b влево:



В случае AVL-деревьев операции вращения повторяются в цикле при восстановлении баланса после добавления или удаления элемента, число вращений не превышает С · h, где h — высота дерева, C — константа. Таким образом, как поиск элемента, так и его добавление или удаление выполняется за логарифмическое время: t <= C · log2n.

Бинарный поиск

Пусть можно сравнивать элементы множества друг с другом, определяя, какой из них больше. (Например, для текстовых строк применяется лексикографическое сравнение: первые буквы сравниваются по алфавиту; если они равны, то сравниваются вторые буквы и т.д.) Тогда можно существенно убыстрить поиск, применяя алгоритм бинарного поиска. Для этого элементы множества хранятся в массиве в возрастающем порядке. Идея бинарного поиска иллюстрируется следующей шуточной задачей: : "Как поймать льва в пустыне? Надо разделить пустыню забором пополам, затем ту половину, в которой находится лев, снова разделить пополам и так далее, пока лев не окажется пойманным".

В алгоритме бинарного поиска мы на каждом шагу делим отрезок массива, в котором может находиться искомый элемент x, пополам. Рассматриваем элемент y в середине отрезка. Если x меньше y, то выбираем левую половину отрезка, если больше, то правую. Таким образом, на каждом шаге размер отрезка массива, в котором может находиться элемент x, уменьшается в два раза. Поиск заканчивается, когда размер отрезка массива (т.е. расстояние между его правым и левым концами) становится равным единице, т.е. через [log2n]+1 шагов, где n — размер массива. В нашем примере это произойдет после 20 шагов (т.к. log21000000 < 20). Таким образом, вместо миллиона операций сравнения при последовательном поиска нужно выполнить всего лишь 20 операций при бинарном.

Запишем алгоритм бинарного поиска на псевдокоде. Дан упорядоченный массив a вещественных чисел (вещественные числа используются для определенности; бинарный поиск можно применять, если на элементах множества определен линейный порядок, т.е. для любых двух элементов можно проверить их равенство или определить, какой их них больше). Пусть текущее число элементов равно n. Элементы массива упорядочены по возрастанию:

a[0] < a[1] < · ·· < a[n - 1]

Мы ищем элемент x. Требуется определить, содержится ли x в массиве. Если элемент x содержится в массиве, то надо определить индекс i ячейки массива, содержащей x:

найти i: a[i] = x

Если же x не содержится в массиве, то надо определить индекс x, такой, что при добавлении элемента x в i-ю ячейку массива элементы массива останутся упорядоченными, т.е.

найти i: a[i-1] < x =< a[i]

(считается, что a[-1] = -?, a[n] = + ?). Объединив оба случая, получим неравенство

a[i-1] < x =< a[i]

Используем схему построения цикла с помощью инварианта. В процессе выполнения хранятся два индекса b и e (от слов begin и end), такие, что

a[b] < x =< a[e]

Индексы b и e ограничивают текущий отрезок массива, в котором осуществляется поиск. Приведенное неравенство является инвариантом цикла. Перед началом выполнения цикла рассматриваются разные исключительные случаи — когда массив пустой (n=0), когда x не превышает минимального элемента массива (x =< a[0]) и когда x больше максимального элемента (x > a[n-1]). В общем случае выполняется неравенство

a[0] < x =< a[n-1])

Полагая b = 0, e = n - 1, мы обеспечиваем выполнение инварианта цикла перед началом выполнения цикла. Условие завершения состоит в том, что длина участка массива, внутри которого может находится элемент x, равна единице:

b - e = 1

В этом случае

a[e-1] < x =< a[e]

т.е. искомый индекс i равен e, а элемент x содержится в массиве тогда и только тогда, когда x = a[e]. В цикле мы вычисляем середину c отрезка [b,e]

с = целая часть ((b+e)/2)

и выбираем ту из двух половин [b,c] или [c,e], которая содержит x. Для этого достаточно сравнить x со значением a[c] в середине отрезка. Завершение цикла обеспечивается тем, что величина e - b монотонно убывает после каждой итерации цикла.

Приведем текст алгоритма бинарного поиска:

лог алгоритм бинарный_поиск( вход: цел n, вещ a[n], вещ x, выход: цел i ) | Дано: n — число элементов в массиве a, | a[0] < a[1] < ... < a[n-1] | Надо: ответ := (x содержится в массиве), | вычислить i, такое, что | a[i-1] < x <= a[i] | (считая a[-1] = -беск., a[n] = +беск.) начало | цел b, e, c; | | // Рассматриваем сначала исключительные случаи | если (n == 0) | | то i = 0; | | ответ := ложь; | иначе если (x <= a[0]) | | i := 0; | | ответ := (x == a[0]); | иначе если (x > a[n-1]) | | i := n | | ответ := ложь; | иначе | | // Общий случай | | утверждение: a[0] < x <= a[n-1]; | | b := 0; e := n-1; | | | | цикл пока e - b > 1 | | | инвариант: a[b] < x и x <= a[e]; | | | c := целая часть((b + e) / 2); | | | если x <= a[c] | | | | то e := c; | | | иначе | | | | b := c; | | | конец если | | конец цикла | | | | утверждение: e - b == 1 и | | a[b] < x <= a[e]; | | i := e; | | ответ := (x == a[i]); | конец если конец алгоритма

Циклы для каждого и итераторы

Часто бывает необходимо перебрать все элементы структуры данных и для каждого элемента выполнить некоторое действие. Обычно при записи алгоритмов на неформальном языке используется конструкция цикл для каждого; например, в случае множества M можно записать следующий фрагмент программы:

цикл для каждого элемента x из множества M | действие(x); конец цикла

В большинстве структур данных такой цикл можно реализовать, пользуясь другими действиями, возможными для структуры этого типа. Например, для списка можно использовать следующий фрагмент программы:

установить указатель в начало списка; цикл пока указатель не в конце списка | действие(элемент за указателем); | передвинуть указатель вперед; конец цикла

Множество отличается от всех других структур данных тем, что цикл для каждого невозможно смоделировать, пользуясь другими предписаниями множества. Поэтому выполнение такого цикла должно быть обеспечено реализацией множества. Метод построения цикла для каждого в сильной степени зависит от используемого языка программирования и от конкретной библиотеки классов или подпрограмм. Как правило, создается некоторый объект, позволяющий последовательно перебирать элементы структуры. Внутреннее устройство такого объекта зависит от структуры данных и скрыто от программиста. Объект такого типа обычно называют итератором или энумератором. С итератором возможны два действия:

проверить, есть ли еще элементы структуры данных, которые не были перебраны на предыдущих шагах; получить следующий элемент структуры данных.

Реализация структуры данных должна обеспечить реализацию предписания, которое создает и инициализирует объект типа итератор, предназначенный для перебора элементов структуры.

В случае множества М цикл для каждого записывается с помощью итератора примерно так:

итератор := начать перебор элементов множества M; цикл пока итератор.есть еще элементы | x := итератор.получить следующий элемент множества; | действие(x); конец цикла

Мы рассмотрели наиболее важные структуры данных, используемые в программировании, и методы их реализации. Конечно, этими примерами не исчерпывается все многообразие структур данных. Однако, большинство реальных примеров либо аналогичны рассмотренным, либо получаются комбинацией нескольких элементарных структур — например, реализация массива множеств может использовать списки или деревья. Искусство программиста состоит в том, чтобы выбрать структуру данных, наиболее подходящую для решаемой задачи, чтобы в ней отсутствовали массовые операции, память расходовалась экономно и поиск выполнялся быстро. И, пожалуй, один из главных критериев — это простота и изящество программы, которая получается в результате.

Деревья и графы

Граф — это фигура, которая состоит из вершин и ребер, соединяющих вершины. Например, схема линий метро — это граф. Ребра могут иметь направления, т.е. изображаться стрелочками; такие графы называются ориентированными. Допустим, надо построить схему автомобильного движения по улицам города. Почти во всех городах есть много улиц с односторонним движением. Поэтому такая транспортная схема должна представляться ориентированным графом. Улице с односторонним движением соответствует стрелка, с двусторонним — пара стрелок в противоположных направлениях. Вершины такого графа соответствуют перекресткам и тупикам.

Дерево — это связный граф без циклов. Кроме того, в дереве выделена одна вершина, которая называется корнем дерева. Остальные вершины упорядочиваются по длине пути от корня дерева.

Зафиксируем некоторую вершину X. Вершины, соединенные с X ребрами и расположенные дальше нее от корня дерева, называются детьми или сыновьями вершины X. Сыновья упорядочены слева направо. Вершины, у которых нет сыновей, называются терминальными. Дерево обычно изображают перевернутым, корнем вверх. .

Деревья в программировании используются значительно чаще, чем графы. Так, на построении деревьев основаны многие алгоритмы сортировки и поиска. Компиляторы в процессе перевода программы с языка высокого уровня на машинный язык представляют фрагменты программы в виде деревьев, которые называются синтаксическими. Деревья естественно применять всюду, где имеются какие-либо иерархические структуры, т.е. структуры, которые могут вкладываться друг в друга. Примером может служить оглавление книги

Пусть книга состоит из частей, части — из глав, главы — из параграфов. Сама книга представляется корнем дерева, из которого выходят ребра к вершинам, соответствующим частям книги. В свою очередь, из каждой вершины-части книги выходят ребра к вершинам-главам, входящим в эту часть, и так далее. Файловую систему компьютера также можно представить в виде дерева. Вершинам соответствуют каталоги (их также называют директориями или папками) и файлы.
Из вершины-каталога выходят ребра к вершинам, соответствующим всем каталогам и файлам, которые содержатся в данном каталоге. Файлы представляются терминальными вершинами дерева. Корню дерева соответствует корневой каталог диска. Программы, осуществляющие работу с файлами, такие, как Norton Commander в системе MS DOS или Проводник Windows, могут изображать файловую систему графически в виде дерева.

Ссылочные реализации как будто специально придуманы для реализации деревьев. Вершина дерева представляется в виде объекта, содержащего ссылки на родительскую вершину и на всех сыновей, а также некоторую дополнительную информацию, зависящую от конкретной задачи. Объект, представляющий вершину дерева, занимает область фиксированного размера, которая обычно размещается в динамической памяти. Число сыновей обычно ограничено, исходя из смысла решаемой задачи. Так, очень часто рассматриваются бинарные деревья, в которых число сыновей у произвольной вершины не превышает двух. Если один или несколько сыновей у вершины отсутствуют, то соответствующие ссылки содержат нулевые значения. Таким образом, у терминальных вершин все ссылки на сыновей нулевые.

При работе с деревьями очень часто используются рекурсивные алгоритмы, т.е. алгоритмы, которые могут вызывать сами себя. При вызове алгоритма ему передается в качестве параметра ссылка на вершину дерева, которая рассматривается как корень поддерева, растущего из этой вершины. Если вершина терминальная, т.е. у нее нет сыновей, то алгоритм просто применяется к данной вершине. Если же у вершины есть сыновья, то он рекурсивно вызывается также для каждого из сыновей. Порядок обхода поддеревьев зависит от сути алгоритма. В главе, посвященной языку Си, уже был рассмотрен простейший рекурсивный алгоритм, подсчитывающий число терминальных вершин бинарного дерева.

Ниже приведен еще один рекурсивный алгоритм, определяющий высоту дерева. Высотой дерева называется максимальная из длин всевозможных путей от корня дерева к терминальным вершинам. Под длиной пути понимается число вершин, входящих в него, включая первую и последнюю вершины.Так, дерево, состоящее из одной корневой вершины, имеет высоту 1, дерево, приведенное на рисунке в начале этого раздела — высоту 4.

цел алгоритм высота_дерева(вход: вершина V) | Дано: V - ссылка на корень поддерева | Надо: Подсчитать высоту поддерева начало | цел h, m, s; | h := 1; | если у вершины V есть сыновья | | то // Ищем поддерево максимальной высоты | | m := 0; | | цикл для каждого сына X вершины V выполнить | | | s := высота_дерева(X); // Рекурсия! | | | если s > m | | | | то m := s; | | | конец если | | конец цикла | | h := h + m; | конец если | ответ := h; конец алгоритма

Хеширование

Рассмотрим другую реализацию множества, в которой поиск элемента чаще всего происходит почти мгновенно. Правда, в исключительных случаях поиск может быть долгим, и поэтому такая реализация не подходит для программ, в которых требуется повышенная надежность, например, при управлении реальными процессами.

Идея хеш-реализации состоит в том, что мы сводим работу с одним большим множеством к работе с массивом небольших множеств. Рассмотрим, к примеру, записную книжку. Она содержит список фамилий людей с их телефонами (телефоны — это нагрузка элементов множества). Страницы записной книжки помечены буквами алфавита; страница, помеченная некоторой буквой, содержит только фамилии, начинающиеся с этой буквы. Таким образом, все множество фамилий разбито на 28 подмножеств, соответствующих буквам русского алфавита. При поиске фамилии мы сразу открываем записную книжку на странице, помеченной первой буквой фамилии, и в результате поиск значительно убыстряется.

Разбиение множества на подмножества осуществляется с помощью так называемой хеш-функции. Хеш-функция определена на элементах множества и принимает целые неотрицательные значения. Она должна быть подобрана таким образом, чтобы 1) ее можно было легко вычислять; 2) она должна принимать всевозможные различные значения приблизительно с равной вероятностью; 3) желательно, чтобы на близких значениях аргумента она принимала далекие друг от друга значения (свойство, противоположное математическому понятию непрерывности). В приведенном примере значение хеш-функции для данной фамилии равно номеру первой буквы фамилии в русском алфавите.

Параметром реализации является число подмножеств, которое также называют размером хеш-таблицы. Пусть он равен N. Тогда хеш-функция должна принимать значения 0, 1, 2, ... , N - 1. Если изначально у нас есть некоторая функция H(x), принимающая произвольные целые неотрицательные значения, то в качестве хеш-функции можно использовать функцию h(x), равную остатку от деления H(x) на N.

Множество M разбивается на N непересекающихся подмножеств, занумерованных индексами от 0 до N - 1.
Подмножество Mi

с индексом i содержит все элементы x из M, значения хеш- функции для которых равняются i:

Mi = {x € M : h(x) = i}

При поиске элемента x сначала вычисляется значение его хеш-функции: t = h(x). Затем мы ищем x в подмножестве Mt

. Поскольку это подмножество небольшое, то поиск осуществляется быстро. Для эффективной реализации каждое подмножество должно в большинстве случаев содержать не больше одного элемента. Следовательно, размер хеш-таблицы N должен быть больше, чем среднее число элементов множества. Обычно N выбирают превышающим число элементов множества примерно в три раза. В примере с записной книжкой это означает, что в ней должно быть записано около 10 фамилий. В таком случае большинство страниц либо пустые, либо содержат одну фамилию, хотя не исключены и коллизии, когда на одной странице записаны несколько фамилий.

Мы привели только идею хеш-реализации множества. Различные конкретные схемы по-разному реализуют массив подмножеств и борются с коллизиями. Приведем наиболее универсальную схему, использующую ссылочную реализацию. Каждое подмножество представляется в виде линейного однонаправленного списка, содержащего элементы подмножества. Таким образом, имеемся N списков. Головы всех списков хранятся в одном массиве размера N, который называется хеш-таблицей. Элемент хеш-таблицы с индексом i представляет собой голову i-го списка. Голова содержит ссылку на первый элемент списка, первый элемент — на второй и так далее. Последний элемент в цепочке содержит нулевую ссылку, т.е. ссылку в никуда. Если список пустой, то элемент хеш-таблицы с индексом i содержит нулевую ссылку.

Красно-черные деревья

Исторически AVL-деревья, изобретенные в 1962 г., были одной из первых схем реализации почти сбалансированных деревьев. В настоящее время, однако, более популярна другая схема: красно-черные деревья, или RB-деревья, от англ. Red-Black Trees. Красно-черные деревья были введены Р. Байером в 1972 г. В стандартной библиотеке классов языка C++ исполнители множество и нагруженное множество — классы set и map — реализованы именно как красно-черные деревья.

Вместо баланс-фактора, применяемого в AVL-деревьях, RB-деревья используют цвета вершин. Каждая вершина окрашена либо в красный, либо в черный цвет. (В реализации за цвет отвечает логическая переменная.) При этом выполняется несколько дополнительных условий:

каждая внешняя (или нулевая) вершина считается черной; корневая вершина дерева черная; у красной вершины дети черные; всякий путь от корня дерева к произвольной внешней вершине имеет одно и то же количество черных вершин.

Последний пункт определения означает сбалансированность дерева по черным вершинам.

Ниже приведен пример красно-черного дерева. Черные вершины изображены темно-серым цветом, красные — белым.

Из пункта 3) определения следует, что в произвольном пути от корня к терминальной вершине не может быть двух красных вершин подряд. Это означает, что, поскольку число черных вершин в любом пути одинаково, длины разных путей к терминальным вершинам отличаются не более чем вдвое. Это свойство близко по своей сути к сбалансированности. Несложно показать, что для красно-черного дерева справедлива следующая оценка сверху на высоту дерева в зависимости от числа вершин:

h <= 2 log2 (n+1)

Из этого следует, что поиск в красно-черном дереве также выполняется за логарифмическое время.

Новая вершина добавляется в красно-черное дерево как терминальная после процедуры поиска (этим RB-дерево ничем не отличается от других упорядоченных деревьев). Новая вершина окрашивается в красный цвет. При этом пункт 3) в определении красно-черного дерева может нарушиться. Поэтому после добавления, а также удаления вершины выполняется процедура восстановления структуры красно-черного дерева, играющая ту же роль, что и восстановление балансировки AVL-дерева. Преимущество красно-черных деревьев состоит в том, что процедура восстановления более простая. Во многих случаях она ограничивается перекрашиванием вершин. В ней также могут выполняться операции вращения вершины влево и вправо, но число вращений может быть не больше двух при добавлении элемента и не больше четырех при удалении. Всего число операций при восстановлении структуры RB-дерева оценивается сверху через высоту дерева:

число операций <= K · h

где h — высота дерева, K — константа. Поскольку для высоты RB-дерева справедлива приведенная выше логарифмическая оценка от числа вершин n, получаем оценку

число операций <= C log2 n

где C - константа. Таким образом, добавление и удаление элементов выполняется в случае красно-черных деревьев за логарифмическое время в зависимости от числа вершин дерева.

Массовые операции

Массовые операции — это операции, затрагивающие значительную часть всех элементов структуры данных. Пусть нужно добавить или удалить один элемент. Если при этом приходится, например, переписывать значительную часть остальных элементов с одного места на другое, то говорят, что добавление или удаление приводит к массовым операциям. Массовые операции — это бедствие для программиста, то, чего он всегда стремится избежать. Хорошая реализация структуры данных — та, в которой массовых операций либо нет совсем, либо они происходят очень редко. Например, добавление элемента должно выполняться за ограниченное число шагов, независимо от того, содержит ли структура десять или десять тысяч элементов.

В непрерывных реализациях добавление или удаление элементов в середине структуры неизбежно приводит к массовым операциям. Поэтому структуры, в которых можно удалять или добавлять элементы в середине, обязательно должны быть реализованы ссылочным образом.

Пример неудачного использования непрерывных реализаций — файловые системы в некоторых старых операционных системах, например, в уже упомянутой ОС ЕС или в системе РАФОС, применявшейся на СМ ЭВМ, на старых советских персональных компьютерах Электроника и т.п. В современных файловых системах файлы фрагментированы, т.е. кусочки большого файла, непрерывного с точки зрения пользователя,на самом деле могут быть разбросаны по всему диску. Раньше это было не так, файлы должны были обязательно занимать непрерывный участок на диске. При постоянной работе файлы уничтожались и создавались заново на новом месте — и всякое редактирование текстового файла приводило к его обновлению. В результате свободное пространство на диске становилось фрагментированным, т.е. состоящим из множества небольших кусков. Возникала ситуация, когда большой файл невозможно записать на диск: хотя свободного места в сумме много, нет достаточно большого свободного фрагмента. Приходилось постоянно выполять длительную и опасную процедуру сжатия диска, которая часто приводила к потере всех данных на нем.

Множество

Множество — это структура данных, содержащая конечный набор элементов некоторого типа. Каждый элемент содержится только в одном экземпляре, т.е. разные элементы множества не равны между собой. Элементы множества никак не упорядочены. В множество M можно добавить элемент x, из множества M можно удалить элемент x. Если при добавлении элемента x он уже содержится в множестве M, то ничего не происходит. Аналогично, никакие действия не совершаются при удалении элемента x, когда он не содержится в множестве M. Наконец, для заданного элемента x можно определить, содержится ли он в множестве M. Множество — это потенциально неограниченная структура, оно может содержать любое конечное число элементов.

В некоторых языках программирования накладывают ограничения на тип элементов и на максимальное количество элементов множества. Так, иногда рассматривают множество элементов дискретного типа, число элементов которого не может превышать некоторой константы, задаваемой при создании множества. (Тип называется дискретным, если все возможные значения данного типа можно занумеровать целыми числами.) Для таких множеств употребляют название Bitset (``набор битов'') или просто Set. Как правило, для реализации таких множеств используется битовая реализация множества на базе массива целых чисел. Каждое целое число рассматривается в двоичном представлении как набор битов, содержащий 32 элемента. Биты внутри одного числа нумеруются справа налево (от младших разрядов к старшим); нумерация битов продолжается от одного числа к другому, когда мы перебираем элементы массива. К примеру, массив из десяти целых чисел содержит 320 битов, номера которых изменяются от 0 до 319. Множество в данной реализации может содержать любой набор целых чисел в диапазоне от 0 до 319. Число N содержится в множестве тогда и только тогда, когда бит с номером N равен единице (программисты говорят бит установлен). Соответственно, если число N не содержится в множестве, то бит с номером N равен нулю (программисты говорят бит очищен).
Пусть, например, множество содержит элементы 0, 1, 5, 34. Тогда в первом элементе массива установлены биты с номерами 0, 1, 5, во втором — бит с номером 2 = 34 - 32. Соответственно, двоичное представление первого элемента массива равно 10011 (биты нумеруются справа налево), второго — 100, это числа 19 и 4 в десятичном представлении. Все остальные элементы массива нулевые.

Хотя в языке программирования Паскаль слово Set, в переводе множество, закреплено за ограниченным множеством элементов дискретного типа, такими множествами далеко не исчерпываются потребности программирования. Например, множество точек на плоскости или множество текстовых строк не являются таковыми. Для множеств общего вида битовая реализация не подходит. Ниже будут рассмотрены несколько других реализаций, используемых для любых множеств.

В программировании довольно часто рассматривают структуру чуть более сложную, чем просто множество: нагруженное множество. Пусть каждый элемент множества содержится в нем вместе с дополнительной информацией, которую называют нагрузкой элемента. При добавлении элемента в множество нужно также указывать нагрузку, которую он несет. В разных языках программирования и в различных стандартных библиотеках такие структуры называют Отображением (Map) или Словарем (Dictionary). Действительно, элементы множества как бы отображаются на нагрузку, которую они несут (заметим, что в математике понятие функции или отображения определяется строго как множество пар; первым элементом каждой пары является конкретное значение аргумента функции, вторым — значение, на которое функция отображает аргумент). В интерпретации Cловаря элемент множества — это иностранное слово, нагрузка элемента — это перевод слова на русский язык (разумеется, перевод может включать несколько вариантов, но здесь перевод рассматривается как единый текст).

Подчеркнем еще раз, что все элементы содержатся в нагруженном множестве в одном экземпляре, т.е. разные элементы множества не могут быть равны друг другу. В отличие от самих элементов, их нагрузки могут совпадать (так, различные иностранные слова могут иметь одинаковый перевод).Поэтому иногда элементы нагруженного множества называют ключами, их нагрузки — значениями ключей. Каждый ключ уникален. Принято говорить, что ключи отображаются на их значения.

В качестве примера нагруженного множества наряду со словарем можно рассмотреть множество банковских счетов. Банковский счет — это уникальный идентификатор, состоящий в случае российских банков из 20 десятичных цифр. Нагрузка счета — это вся информация, которая ему соответствует, включающая имя и адрес владельца счета, код валюты, сумму остатка, информацию о последних транзакциях и т.п.

Наиболее часто применяемая операция в нагруженном множестве — это определение нагрузки для заданного элемента x (значения ключа x). Реализация этой операции включает поиск элемента x в множестве, поэтому эффективность любой реализации множества определяется прежде всего быстротой поиска.

Реализации множества на базе деревьев

Реализация множества с помощью бинарного поиска во всех отношениях лучше наивной реализации. Вместе с тем, она все же имеет недостатки: 1) при добавлении и удалении элементов в середине массива приходится переписывать элементы в конце массива на новое место, чтобы освободить место для добавляемого элемента либо закрыть образовавшуюся лакуну при удалении элемента; 2) поиск выполняется гарантированно быстро, но все-таки не мгновенно. От первого из этих недостатков можно избавиться, применяя вместо непрерывной реализации на базе массива ссылочную реализацию, при которой элементы множества содержатся в вершинах бинарного дерева. Элементы в вершинах упорядочены таким образом, что, если зафиксировать некоторую вершину V и рассмотреть два поддерева, соответствующих левому и правому сыновьям вершины, то все элементы в вершинах левого поддерева должны быть меньше, чем элемент в вершине V, а все элементы в вершинах правого поддерева должны быть больше него.

Для такого дерева можно также применять алгоритм бинарного поиска. Максимальное число сравнений при поиске в таком дереве равняется его высоте ( т.е. максимальной длине пути от корня к терминальной вершине).

Чтобы поиск выполнялся быстро, дерево должно быть сбалансированным, т.е. все его ветви должны иметь почти одинаковую длину.

Точное определение сбалансированности следующее: будем считать, что у каждой вершины, включая терминальные, ровно два сына, при необходимости добавляя внешние, или нулевые, вершины. Например, у терминальной вершины оба сына нулевые. (Это в точности сответствует представлению дерева в языке Си, где каждая вершина хранит два указателя на сыновей; если сына нет, то соответствующий указатель нулевой.) Обычные вершины дерева будем называть собственными. Рассмотрим путь от корня дерева к внешней (нулевой) вершине. Длиной пути считается количество собственных вершин в нем. Дерево называется сбалансированным, если длины всех возможных путей от корня дерева к внешним вершинам различаются не более чем на единицу.
Иногда в литературе такие деревья называют почти сбалансированными, понимая под сбалансированностью строгое равенство длин всех путей от корня к внешним узлам; мы, однако, будем придерживаться нестрогого определения. Пример сбалансированного дерева представлен на рисунке.

Высота сбалансированного дерева h оценивается логарифмически в зависимости от числа вершин n:

h <= log2n + 1

Поскольку максимальное число сравнений при поиске элемента в упорядоченном бинарном дереве равняется высоте дерева, поиск в сбалансированном дереве осуществляется исключительно быстро, за время, логарифмически зависящее от числа элементов множества. (Можно доказать, что это является теоретической оценкой снизу: никакой алгоритм не может в общем случае находить элемент быстрее, чем за log2n операций.)

Для эффективной реализации множества на базе дерева процедуры добавления и удаления элементов должны сохранять свойство сбалансированности (или почти сбалансированности). Рассмотрим коротко две наиболее популярные схемы реализации.

Реализации множества: последовательный и бинарный поиск, хеширование

Рассмотрим для простоты реализацию обычного, не нагруженного, множества. (Реализация нагруженного множества аналогична реализации обычного, просто параллельно с элементами нужно дополнительно хранить нагрузки элементов.) В наивной реализации множества его элементы хранятся в массиве, начиная с первой ячейки. Специальная переменная содержит текущее число элементов множества, т.е. количество используемых в данный момент ячеек массива.

При добавлении элемента x к множеству сначала необходимо определить, содержится ли он в множестве (если содержится, то множество не меняется). Для этого используется процедура поиска элемента, которая отвечает на вопрос, принадлежит ли элемент x множеству, и, если принадлежит, выдает индекс ячейки массива, содержащей x. Та же процедура поиска используется и при удалении элемента из множества. При добавлении элемента он дописывается в конец (в ячейку массива с индексом число элементов) и переменная число элементов увеличивается на единицу. Для удаления элемента достаточно последний элемент множества переписать на место удаляемого и уменьшить переменную число элементов на единицу.

В наивной реализации элементы множества хранятся в массиве в произвольном порядке. Это означает, что при поиске элемента x придется последовательно перебрать все элементы, пока мы либо не найдем x, либо не убедимся, что его там нет. Пусть множество содержит 1,000,000 элементов. Тогда, если x содержится в множестве, придется просмотреть в среднем 500,000 элементов, если нет — все элементы. Поэтому наивная реализация годится только для небольших множеств.

Список

Классический пример структуры данных последовательного доступа, в которой можно удалять и добавлять элементы в середине структуры, — это линейный список. Различают однонаправленный и двунаправленный списки (иногда говорят односвязный и двусвязный).

Элемены списка как бы выстроены в цепочку друг за другом. У списка есть начало и конец. Имеется также указатель списка, который располагается между элементами. Если мысленно вообразить, что соседние элементы списка связаны между собой веревкой, то указатель — это ленточка, которая вешается на веревку. В любой момент времени в списке доступны лишь два элемента — элементы до указателя и за указателем.

В однонаправленном списке указатель можно передвигать лишь в одном направлении — вперед, в направлении от начала к концу. Кроме того, можно установить указатель в начало списка, перед его первым элементом. В отличие от однонаправленного списка, двунаправленный абсолютно симметричен, указатель в нем можно передвигать вперед и назад, а также устанавливать как перед первым, так и за последним элементами списка.

В двунаправленном списке можно добавлять и удалять элементы до и за указателем. В однонаправленном списке добавлять элементы можно также с обеих сторон от указателя, но удалять элементы можно только за указателем.

Удобно считать, что перед первым элементом списка располагается специальный пустой элемент, который называется головой списка. Голова списка присутствует всегда, даже в пустом списке. Благодаря этому можно предполагать, что перед указателем всегда есть какой-то элемент, что упрощает процедуры добавления и удаления элементов.

В двунаправленном списке считают, что вслед за последним элементом списка вновь следует голова списка, т.е. список зациклен в кольцо.

Можно было бы точно так же зациклить и однонаправленной список. Но гораздо чаще считают, что за последним элементом однонаправленного списка ничего не следует. Однонаправленный список, таким образом, представляет собой цепочку, начинающуюся с головы списка, за которой следует первый элемент, затем второй и так далее вплоть до последнего элемента, а заканчивается цепочка ссылкой в никуда.

Ссылочная реализация списка

Мы рассмотрели абстрактное понятие списка. Но в программировании зачастую отождествляют понятие списка с его ссылочной реализацией на базе массива или непосредственно на базе оперативной памяти.

Основная идея реализации двунаправленного списка заключается в том, что вместе с каждым элементом хранятся ссылки на следующий и предыдущий элементы. В случае реализации на базе массива ссылки представляют собой индексы ячеек массива. Чаще, однако, элементы списка не располагают в каком-либо массиве, а просто размещают каждый по отдельности в оперативной памяти, выделенной данной задаче. (Обычно элементы списка размещаются в так называемой динамической памяти, или куче — это область оперативной памяти, в которой можно при необходимости захватывать куски нужного размера, а после использования освобождать, т.е. возвращать обратно в кучу.) В качестве ссылок в этом случае используют адреса элементов в оперативной памяти.

Голова списка хранит ссылки на первый и последний элементы списка. Поскольку список зациклен в кольцо, то следующим за головой списка будет его первый элемент, а предыдущим — последний элемент. Голова списка хранит только ссылки и не хранит никакого элемента. Это как бы пустой ящик, в который нельзя ничего положить и который используется только для того, чтобы написать на нем адреса следующего и предыдущего ящиков, т.е. первого и последнего элементов списка. Когда список пуст, голова списка зациклена сама на себя.

Указатель списка реализуется в виде ссылки на следующий и предыдущий элементы, он просто отмечает некоторое место в цепочке элементов.

В случае однонаправленного списка хранится только ссылка на следующий элемент, таким способом экономится память. Голова однонаправленного списка хранит ссылку на первый элемент списка. Последний элемент списка хранит нулевую ссылку, т.е. ссылку в никуда, т.к. в программах нулевой адрес никогда не используется.

Ценность ссылочной реализации списка состоит в том, что процедуры добавления и удаления элементов не приводят к массовым операциям. Рассмотрим, например, операцию удаления элемента за указателем. Читая ссылку на следующий элемент в удаляемом элементе, мы находим, какой элемент должен будет следовать за указателем после удаления текущего элемента. После этого достаточно связать элемент до указателя с новым элементом за указателем. А именно, обозначим через X адрес элемента до указателя, через Y — адрес нового элемента за указателем. В поле следующий для элемента с адресом X надо записать значение Y, в поле предыдущий для элемента с адресом Y — значение X. Таким образом, при удалении элемента за указателем он исключается из цепочки списка, для этого достаточно лишь поменять ссылки в двух соседних элементах. Аналогично, для добавления элемента достаточно включить его в цепочку, а для этого также нужно всего лишь модифицировать ссылки в двух соседних элементах. Добавляемый элемент может располагаться где угодно, следовательно, нет никаких проблем с захватом и освобождением памяти под элементы.

Ссылочные реализации структур данных

Большинство структур данных реализуется на базе массива. Все реализации можно разделить на два класса: непрерывные и ссылочные. В непрерывных реализациях элементы структуры данных располагаются последовательно друг за другом в непрерывном отрезке массива, причем порядок их расположения в массиве соответствует их порядку в реализуемой структуре. Рассмотренные выше реализации очереди и стека относятся к непрерывным.

В ссылочных реализациях элементы структуры данных хранятся в произвольном порядке. При этом вместе с каждым элементом хранятся ссылки на один или несколько соседних элементов. В качестве ссылок могут выступать либо индексы ячеек массива, либо адреса памяти. Можно представить себе шпионскую сеть, в которой каждый участник знает лишь координаты одного или двух своих коллег. Контрразведчикам, чтобы обезвредить сеть, нужно пройти последовательно по всей цепочке, начиная с выявленного шпиона.

Ссылочные реализации обладают двумя ярко выраженными недостатками: 1) для хранения ссылок требуется дополнительная память; 2) для доступа к некоторому элементу структуры необходимо сначала добраться до него, проходя последовательтно по цепочке других элементов. Казалось бы, зачем нужны такие реализации?

Все недостатки ссылочных реализаций компенсируются одним чрезвычайно важным достоинством: в них можно добавлять и удалять элементы в середине структуры данных, не перемещая остальные элементы.

---

---