) Природа данных
Все данные представляются в форме символьных выражений. В Лиспе Дж. Мак-Карти назвал их S-выражениями. Состав S-выражений и типы их элементов не ограничиваются, что позволяет его использовать как древообразные структуры. Это позволяет локализовывать любые важные подвыражения. Система программирования над такими структурами обычно использует для их хранения всю доступную память, поэтому программист освобожден от распределения памяти под отдельные блоки данных.
) Самоописание обработки символьных выражений
Важная особенность функционального программирования состоит в том, что описание способов обработки S-выражений представляется программами, рассматриваемыми как символьные данные. Программы строятся из рекурсивных функций над S-выражениями. Определения и вызовы этих функций, как и любая информация, имеют вид S-выражений, то есть формально они могут обрабатываться как обычные данные, получаться в процессе вычислений и преобразовываться как значения.
) Подобие машинным языкам
Система функционального программирования допускает, что программа может интерпретировать и/или компилировать программы, представленные в виде S-выражений. Это сближает методы функционального программирования с методами низкоуровнего программирования и отличает от традиционной методики применения языков высокого уровня.
Не все языки функционального программирования в полной мере допускают эту возможность, но для Лиспа она весьма характерна. В принципе, такая возможность достижима на любом стандартном языке, но так делать не принято.
Наиболее очевидные следствия из выбранных принципов:
процесс разработки программ разбивается на две фазы: построение базиса и его пошаговое расширение;рассмотрение программы как реализации алгоритма естественно дополняется табличной реализацией функций, т.е. допустимо использование хранимых графиков функций в виде структур из аргументов и соответствующих результатов наряду с процедурами;прозрачность ссылок обеспечена совпадением значений одинаково выглядящих формул, вычисляемых в одинаковом контексте;нацеленность на универсальные функции и функционально полные системы, трудоемкость первичной реализации которых компенсируется надежностью определений и простотой применения.
Функциональное программирование активно применяется для генерации программ и выполнения динамически конструируемых прототипов программ, а также для систем, применяемых в областях с низкой кратностью повторения отлаженных решений (например, в учебе, проектировании, творчестве и научных исследованиях), ориентированных на оперативные изменения, уточнения, улучшения, адаптацию и т.п.
Данные
Любые структуры данных начинаются с элементарных значений. Следуя Лиспу, в функциональном программировании такие значения называют атомами или символами. Внешне атом обычно выглядит как последовательность из букв и цифр, начинающаяся с буквы. В первых реализациях Лиспа было принято ограничивать длину атома, но ограничение было не слишком жестким (30 литер). Теперь ограничивают лишь число значащих литер (порядка 60), по которым атомы распознаются как различимые объекты с помощью хэш-таблицы объектов.
A ATOM ВотВесьмаДлинныйАтомНоЕслиНадоМожетБытьЕщеДлинннее Ф4длш139к131б
Одинаково выглядящие атомы не различимы по своим свойствам, хотя проявления этих свойств могут быть обусловлены контекстом использования атомов. Термин "атом" выбран по аналогии с химическими атомами. Согласно этой аналогии атом может иметь достаточно сложное строение, но оно не рассматривается как обычное S-выражение. Устройство атома реализационно зависимо и лишь соответствует некоторой спецификации, содержание которой будет рассмотрено в девятой лекции. Атом не предназначен для разбора на части базовыми средствами языка.
Более сложные данные выстраиваются из унифицированных структур данных — одинаково устроенных блоков памяти. В Лиспе это бинарные узлы, содержащие пары объектов произвольного вида. Каждый бинарный узел соответствует минимальному блоку памяти, выделяемому системой программирования при организации и обработке структур данных. Выделение блока памяти и размещение в нем пары данных выполняет функция CONS (от слова consolidation), а извлечение левой и правой частей из блока выполняют функции CAR и CDR, соответственно. (В других языках функционального программирования используются векторы, кортежи, последовательности, потоки, множества, сети и другие структуры данных, обладающие достаточной гибкостью, т.е. способностью к организации единого доступа к любому числу элементов произвольного типа.)
CONS =>> [CAR | CDR]
Бинарный узел, содержащий пару атомов ATOM и Nil, рассматривается как одноэлементный список:
(ATOM) = [ ATOM | Nil ]
Если вместо атома ATOM рекурсивно подставлять произвольные атомы, а вместо Nil — произвольные списки, затем вместо ATOM — построенные списки и так далее, то мы получим множество всех возможных списков. Атом Nil играет роль пустого списка и фактически эквивалентен ему. Можно сказать, что список — это заключенная в скобки последовательность из атомов, разделенных пробелами, или списков.
ATOM (A B) (A B C D E F G H I J K L M N O P R S T U V W X Y Z) (C (A B)) ((A B) C) ((A B) (D C)) ((A B)(D(C E)))
Такая форма представления информации называется списочной записью (list-notation). Ее основные достоинства — лаконичность, удобство набора и отсутствие "синтаксического сахара". Она достаточно отражает взаимосвязи структур данных, размещаемых в памяти, и помогает задавать процедуры доступа к их компонентам.
Любой список может быть построен из пустого списка и атомов с помощью CONS, и любая его часть может быть выделена с помощью подходящей композиции CAR-CDR.
Функция CONS строит списки из бинарных узлов, заполняя их парами объектов, являющихся значениями пары ее аргументов. Первый аргумент произвольного вида размещается в левой части бинарного узла, а второй, являющийся списком, — в правой.
Функция CAR обеспечивает доступ к первому элементу списка — его "голове", а функция CDR — к укороченному на один элемент списку — его "хвосту", т.е. к тому, что остается после удаления головы.
Функция ATOM позволяет различать составные и атомарные
объекты: на атомах ее значение "истина", а на структурированных объектах — "ложь".
Функция EQ выполняет проверку атомарных объектов на равенство.
Различие истинностных значений в Лиспе принято отождествлять с разницей между пустым списком и остальными объектами, которым программист может придать в программе некоторый другой смысл. Таким образом, значение "ложь" — это всегда Nil. (Во многих языках программирования используется 0 – 1 или идентификаторы True — False и др.)
Если требуется явно изобразить истинностное значение, то для определенности в качестве значения "истина" используется константа — атом T (true) как стандартное представление, но роль такого значения может выполнить любой, отличный от пустого списка, объект.
Основные понятия: программа, функции и выражения
Гипотезу об универсальности символьных данных, прежде всего, следует проверить при выборе представления форм, возникающих при написании программы и ее основного конструктива — переменных, констант, выражений, определений, ветвлений, вызовов функций:
1) Самая простая форма выражения — это переменная. Она может быть представлена как атом.
X Y n Variablel LongSong
2) Более сложные формы могут пониматься как применение функции к ее аргументам (вызов функции). Аргументом функции может быть любая форма. Вызов функции можно строить как список, первый элемент которого — представление функции, остальные элементы — аргументы функции.
(функция аргумент1 аргумент2 ... )
Обычно S-выражение — это или атом, или список; значит, неатомарное S-выражение можно понимать как вызов функции, если все остальные понятия свести к применению некоторых функциональных объектов.
Теперь можно записывать формы для получения результатов операций из таблиц 2.1 и 2.2 в виде списков:
(ATOM Nil) (CONS Nil Nil ) ((LAMBDA (Y X) (CONS X Y)) Nil (ATOM Nil)) ;= (T) ((LAMBDA (X Y) (CONS X Y)) Nil (ATOM Nil)) ;= (() . T)
";" - начало строчного комментария. Последние два примера показывают роль порядка аргументов функции, задаваемого с помощью специального LAMBDA-конструктора.
3) Имена функций, как и переменных, лучше всего изображать с помощью атомов, для наглядности можно выбирать заглавные буквы.
Соответствие между именем функции и ее определением можно задать с помощью специального конструктора функций LABEL (отсутствует в Common Lisp), первый аргумент которого — имя функции, второй — собственно именуемое определение функции. Формальным результатом LABEL является ее первый аргумент, который становится объектом другой категории. Он меняет свой статус — теперь это имя новой функции.
(LABEL третий ; имя новой функции (LAMBDA (x) ; параметры функции (CAR (CDR (CDR x))) ; тело функции ) )
Пример 2.1.
Новая функция "третий" действует так же, как "Cadadr" в таблице 2.4. Именование функций работает подобно присваиванию значений переменным, но идентификатору присваивается объект другой категории — структура, символизирующая функциональный объект, содержащая список формальных параметров функции и тело ее определения.
По отношению к процессам обработки данных разница между константами и переменными заключается лишь в том, что значение переменной может быть в любой момент изменено, а константа изменяется существенно реже. Обычно в рассуждениях о переменных и константах подразумевается, что речь идет лишь о данных. Поскольку функциональное программирование рассматривает представления функций как данные, постольку и функции могут быть как константными, так и переменными. Представления функции могут вычисляться и передаваться как параметры или результаты других функций. Соответствие между именем функции и ее определением может быть изменено, подобно тому, как меняется соответствие между именем переменной и ее значением.
4) Композиции функций можно строить с помощью вложенных скобок.
(функция1 (функция2 аргумент21 аргумент22 ... ) аргумент2 ... )
Приведенные правила ничего не говорят ни о природе данных и функций, ни о порядке вычисления аргументов и композиций функций. Речь идет исключительно о форме — внешнем виде списков, используемых для записи программы. Такая синтаксическая оболочка, в которой еще не конкретизированы операции над данными, является общей спецификацией реализационной основы для определения аппликативных систем, допускающих специализацию практически в любом направлении. Можно сказать, что Лисп является аппликативной системой, специализированной для обработки списков или S-выражений. (Язык функционального программирования Sisal [11] специализирован для обработки многомерных векторов и организации параллельных процессов, выполняемых на суперкомпьютерах.)
Этих правил достаточно, чтобы более ясно выписать основные тождества Лиспа, формально характеризующие элементарные функции CAR, CDR, CONS, ATOM, EQ над S-выражениями:
(CAR (CONS x y)) ; = x (CDR (CONS x y)) ; = y (ATOM (CONS x y)) ; = Nil (CONS (CAR x) (CDR x)) ; = x для неатомарных x. (EQ x x) ; = T если x атом (EQ x y) ; = Nil если x и y различимы
Любые композиции заданного набора функций над конечным множеством произвольных объектов можно представить таким способом, но класс соответствующих им процессов весьма ограничен и мало интересен.
Организация более сложного класса процессов требует более детального представления в программах соответствия между именами и их значениями или определениями, изображения ветвлений и объявления констант.
5) Традиция при изучении функционального программирования избегать знакомства с явными средствами объявления значений переменных ради формирования навыков задания таких значений как аргументов функций малосостоятельна, т.к. изменение переменных легко моделируется переопределением функций без аргументов. Поэтому признаем сразу, что значение переменной можно объявить специальной функцией SET.
(Set 'PI 3.1415926)
6) Обычно в системы программирования встраивают наиболее часто используемые константы. Некоторые атомы изначально имеют определенный смысл, например, базовые функции, представление пустого списка Nil и тождественно истинная константа T
В зависимости от контекста одни и те же объекты могут играть роль переменных или констант, причем значения и того, и другого могут быть произвольной сложности. Если объект играет роль константы, то для объявления константы достаточно заблокировать его вычисление, то есть как бы взять его в кавычки (quotation), отмечающие буквально используемые фразы, нетребующие обработки. Для такой блокировки вводится специальная функция QUOTE, предохраняющая свой единственный аргумент от вычисления.
(QUOTE A) ; константа атом A (QUOTE (A B C) ) ; константа список (A B C) (ATOM (QUOTE A)) ; = T — аргумент предиката - атом A (ATOM (QUOTE (A B C) )) ; = Nil — аргумент предиката - список (A B C) (ATOM A) ;— значение не определено
Оно зависит от вхождения переменной A, а ее значение зависит от контекста и должно быть определено или задано до попытки выяснить, атом ли это.
Можно сказать, что функция QUOTE выполняет в древовидной структуре программы роль помеченного контейнера. С ее помощью любое выражение может быть заключено в контейнер, а контейнер помечен указанием, что вычислять его содержимое не следует. Потом, при выполнении функции QUOTE, пометка и контейнер исчезают, и выражение может обрабатываться по общей схеме.
Например: (третий (QUOTE (A B C))) — применение функции "третий" к значению, не требующему вычисления.
7) Некоторые определения функций могут быть хорошо определены на одних аргументах, но зацикливаться на других, подобно традиционному определению факториала при попытке применить его к отрицательным числам. Результат может выглядеть как исчезновение свободной памяти или слишком долгий счет без видимого прогресса. Такие функции называют частичными. Их определения должны включать в себя ветвления для проверки аргументов на принадлежность фактической области определения функции — динамический контроль. Точнее, вычисление ряда форм в определении может быть обусловлено заранее заданными предикатами.
Ветвление (условное выражение) характеризуется тем, что ход процесса зависит от некоторых предикатов (условий), причем условия следует сгруппировать в общий комплект и соотнести с подходящими ветвями. Такую организацию процесса вычисления обеспечивает специальная функция COND (condition), аргументами которой являются двухэлементные списки, содержащие предикаты и соответствующие им выражения. Аргументов может быть сколько угодно, а обрабатываются они по особой схеме: сначала вычисляются первые элементы аргументов по порядку, пока не найдется предикат со значением "истина". Затем выбирается второй элемент этого аргумента, и вычисляется его значение, которое и считается значением всего условного выражения.
(COND (p1 e1) (p2 e2) ... (pk ek) )
pi - предикаты для выбора ветви,
ei - ветви условного выражения
Каждый предикат pi или ветвь ei может быть любой формы: переменная, константа, вызов функции, композиция функций, условное выражение.
Обычное условное выражение (if Predicate Then Else) или (если Predicate то Then иначе Else) может быть представлено с помощью функции COND следующим образом:
(COND (Predicate Then)(T Else))
Разумеется, можно повышать наглядность подбором геометрии текста:
(COND (Predicate Then) (T Else) )
(COND ((EQ (CAR x) (QUOTE A)) (CONS (QUOTE B) (CDR x)) ) (T x) )
Пример 2.2.
Атом T представляет тождественную истину. Значение всего условного выражения получается путем замены первого элемента из значения переменной x на B в том случае, если (CAR x) совпадает с A
Содержательно функции QUOTE, COND, LAMBDA образуют базовый комплект средств управления программами и процессами, поддерживающий стиль программирования, идеологически близкий структурному программированию [18].
Такие специальные функции QUOTE, COND, LAMBDA существенно отличаются от элементарных функций CAR, CDR, CONS, ATOM, EQ правилом обработки аргументов. Обычные функции получают значения аргументов, предварительно вычисленные системой программирования по формулам фактических параметров функции. Специальные функции не требуют такой предварительной обработки параметров. Они сами могут выполнять все необходимое, используя представление фактических параметров в виде S-выражений.
Основы символьной обработки. Базовые средства
Функциональный стиль программирования сложился в практике решения задач символьной обработки данных в предположении, что любая информация для компьютерной обработки может быть сведена к символьной. (Существование аналоговых методов принципиально не противоречит этой гипотезе.) Слово "символ" здесь близко понятию "знак" в знаковых системах. Информация представляется символами, смысл которых может быть восстановлен по заранее известным правилам.
Методы функционального программирования основаны на формальном математическом языке представления и преобразования формул. Поэтому можно дать точное, достаточно полное описание основ функционального программирования и специфицировать систему программирования для поддержкии разработки разных парадигм программирования, моделируемых с помощью функционального подхода к организации деятельности.
Такое определение будет приведено в шестой лекции, а сейчас необходимо освоить технические приемы символьной обработки. В дальнейшем будут проиллюстрированы и практические способы применения функционального программирования, превращающие его в удобную технологию современного программирования.
Функциональное программирование отличается от большинства подходов к программированию тремя важными принципами:
имя новой функции
| (LABEL третий ; имя новой функции (LAMBDA (x) ; параметры функции (CAR (CDR (CDR x))) ; тело функции ) ) |
| Пример 2.1. |
| Закрыть окно |
| (COND ((EQ ( CAR x) (QUOTE A)) (CONS (QUOTE B) (CDR x)) ) (T x) ) |
| Пример 2.2. |
| Закрыть окно |
| (LABEL премьер ; имя локальной функции (LAMBDA (x) ; определение функции (COND ((ATOM x) x) (T (премьер (CAR x))) ) ) ) |
| Пример 2.3. |
| Закрыть окно |
| ( LABEL Абс (LAMBDA (x) (COND ((< x 0 ) (- x)) (T x) ) ) ) |
| Пример 2.4. Абсолютное значение числа |
| Закрыть окно |
| ( LABEL Факториал (LAMBDA (N) (COND ((= N 0 ) 1 ) (T ( * N (Факториал (- N 1 ))) ) ) ) ) |
| Пример 2.5. Факториал неотрицательного числа |
| Закрыть окно |
| (LABEL НОД (LAMBDA (x y) (COND ((< x y) (НОД y x)) ((= (остаток y x ) 0 ) x ) (T (НОД (остаток y x) x )) ) ) ) |
| Пример 2.6. Алгоритм Евклида для нахождения наибольшего общего делителя двух положительных целых чисел (остаток [x, y] — функция, вычисляющая остаток от деления x на y). |
| Закрыть окно |
| (DEFUN третий ; имя новой функции (x) ; параметры функции (CAR (CDR (CDR x ))) ; тело функции ) |
| Пример 2.7. |
| Закрыть окно |
Рекурсивные функции: определение и исполнение
8) Определения могут быть рекурсивными.
На практике такие определения обычно имеют глобальные имена, задаваемы с помощью функции DEFUN, о которой еще будет речь в конце этой лекции. Сейчас теоретически можно ограничиться конструктором локальных функций LABEL, которую мы вводим здесь для учебных целей (в системе GNU Clisp его нет, но для него проще определение интерпретатора, которое будем строить в следующей лекции).
Как правило, рекурсивные вызовы функций должны быть заданы в комплекте с нерекурсивными ветвями процесса. Основное применение условных выражений — рекурсивные определения функций.
(LABEL премьер ; имя локальной функции (LAMBDA (x) ; определение функции (COND ((ATOM x) x) (T (премьер (CAR x))) ) ) )
Пример 2.3.
Новая функция "премьер" выбирает первый атом из любого данного. Если x является атомом, то он является результатом, иначе функцию "премьер" следует применить к первому элементу значения x, которое получается в результате вычисления формулы (CAR x). На составных x будет выполняться вторая ветвь, выбираемая по тождественно истинному значению встроенной константы T.
Определение функции "премьер" рекурсивно. Эта функция действительно работает в терминах самой себя. Важно, что для любого S-выражения существует некоторое число применений функции CAR, после которого из этого S-выражения выделится какой-нибудь атом, следовательно, процесс вычисления функции всегда определен, детерминирован и завершится за конечное число шагов. Можно сказать, что для определенности рекурсивной функции следует формулировать условие ее завершения.
Введенные обозначения достаточны, чтобы проследить за формированием значений и преобразованием форм в процессе исполнения функциональных программ. Рассмотрим вычисление формы:
((LABEL премьер (LAMBDA (x) (COND ((ATOM x) x) (T (премьер (CAR x))) ) ) ) ; объявлена локальная функция "премьер" (QUOTE ((A . B) . C) ) ; дан аргумент локальной функции ) ; завершено выражение с локальной функцией
Точечная нотация
Исторически при реализации Лиспа в качестве единой базовой структуры для конструирования S-выражений использовалась так называемая "точечная нотация" (dot-nоtation), согласно которой левая и правая части бинарного узла равноправны и могут хранить данные любой природы.
Бинарный узел, содержащий пару атомов ATOM1 и ATOM2, можно представить в виде S-выражения вида:
( ATOM1 . ATOM2 )
|
CONS |
A и Nil |
(A ) |
|
CONS |
(A B) и Nil |
((A B) ) |
|
CONS |
A и (B) |
(A B) |
|
CONS | (Результат предыдущего CONS) и (C) |
((A B) C) |
|
CONS |
A и (B C) |
(A B C) |
|
CAR |
(A B C) |
A |
|
CAR |
(A (B C)) |
A |
|
CAR |
((A B) C) |
(A B) |
|
CAR |
A | не определен |
|
CDR |
(A ) |
Nil |
|
CDR |
(A B C D) |
(B C D) |
|
CDR |
(A (B C)) |
((B C)) |
|
CDR |
((A B) C) |
(C) |
|
CDR |
A | не определен |
|
CDR |
(A B C) |
(B C) |
|
CAR | результат предыдущего CDR |
B |
|
CAR |
(A C) |
A |
|
CAR | результат предыдущего CAR | не определен |
|
CONS |
A и (B) |
(A B) |
|
CAR | результат предыдущего CONS |
A |
|
CONS |
A и (B) |
(A B) |
|
CDR | результат предыдущего CONS |
(B) |
|
ATOM |
VeryLongStringOfLetters |
T |
|
CDR |
(A B) |
(B) |
|
ATOM | результат предыдущего CDR |
Nil |
|
ATOM |
Nil |
T |
|
ATOM |
( ) |
T |
|
EQ |
A A |
T |
|
EQ |
A B |
Nil |
|
EQ |
A (A B) |
Nil |
|
EQ |
(A B) (A B) | не определен |
|
EQ |
Nil и ( ) |
T |
Если вместо атомов ATOM1, ATOM2 рекурсивно подставлять произвольные атомы, затем построенные из них пары и так далее, то получим множество всех возможных S-выражений. Можно сказать, что S-выражение — это или атом или заключенная в скобки пара из двух S-выражений, разделенных точкой. Все сложные данные выстраиваются из одинаково устроенных блоков — бинарных узлов, содержащих пары объектов произвольного вида. Каждый бинарный узел соответствует минимальному блоку памяти.
ATOM (A . B) (C . (A . B)) ((A . B) . C) ((A . B) . (D . C)) ((A .
B) . (D . (C . E)))
Любое S- выражение может быть построено из атомов с помощью CONS, и любая его часть может быть выделена с помощью CAR-CDR.
Расширение типа данных, допускаемых в качестве второго аргумента CONS, ни в малейшей степени не усложняет реализацию этой функции, равно как и реализацию функций CAR и CDR, зато их описания становятся проще. Функция CONS строит бинарный узел и заполняет его парой объектов, являющихся значениями пары ее аргументов. Первый аргумент размещается в левой части бинарного узла, а второй — в правой. Функция CAR обеспечивает доступ к объектам, расположенным слева от точки, а функция CDR — справа.
CONS | A и B | (A . B) |
CONS | (A . B) и C | ((A . B) . C) |
CONS | A B | (A . B) |
CONS | (результат предыдущего CONS) и C | ((A . B) . C) |
CAR | (A . B) | A |
CAR | ((A . B) . C) | (A . B) |
CDR | (A . B) | B |
CDR | (A . (B . C)) | (B . C) |
CONS | A и B | (A . B) |
CAR | результат предыдущего CONS | A |
CONS | A и B | (A . B) |
CDR | результат предыдущего CONS | B |
CDR | (A . (B . C)) | (B . C) |
CAR | результат предыдущего CDR | B |
CDR | (A . C) | C |
CAR | результат предыдущего CDR | не определен |
CONS | два произвольных объекта x и y | (x . y) |
CAR | результат предыдущего CONS | исходный объект x (первый аргумент CONS) |
CONS | два произвольных объекта x и y | (x . y) |
CDR | результат предыдущего CONS | исходный объект y (второй аргумент CONS) |
CAR | произвольный составной объектx | (CAR x) |
CDR | тот же самый объект x - не атом | (CDR x) |
CONS | результаты предыдущих CAR и CDR | исходный объект x |
ATOM | (A . B) | Nil - выполняет роль ложного значения |
CDR | (A . B) | B |
ATOM | результат предыдущего CDR | T |
EQ | (A . B) (A . B) | не определен |
Практически сразу была предложена более лаконичная запись наиболее употребимого подкласса S-выражений в виде списков произвольной длины вида (A B C D E F G H ). В виде списков можно представить лишь те S-выражения, в которых при движении вправо в конце концов обнаруживается атом Nil, символизирующий завершение списка.
Атом Nil, рассматриваемый как представление пустого списка (), играет роль ограничителя в любом списке. Одноэлементный список (A) идентичен S-выражению (A . Nil). Список (A1 A2 ... Ak) может быть представлен как S-выражение вида:
(A1 . (A2 . ( ... . (Ak . Nil) ... ))).
В памяти это фактически одна и та же структура данных. (Запятая в качестве разделителя элементов списка в первых реализациях Лиспа поддерживалась, но не прижилась. Пробел оказался удобнее.)
Для многошагового доступа к отдельным элементам такой структуры удобно пользоваться мнемоничными обозначениями композиций из многократных CAR-CDR. Имена таких композиций устроены как цепочки из "a" или "d", задающие маршрут движения из шагов CAR и CDR, соответственно, расположенный между "c" и "r". Указанные таким способом CAR-CDR исполняются с ближайшего к аргументу шага, т.е. в порядке, обратном записи.
(A B C) | (A . (B . (C . Nil))) |
((A B) C) | ((A . (B . Nil)) . (C . Nil)) |
(A B (C E)) | (A . (B . ((C . (E . Nil)). Nil))) |
(A) | (A . Nil) |
((A)) | ((A . Nil) . Nil) |
(A (B . C)) | (A . ((B . C) . Nil)) |
(()) | (Nil . Nil) |
Caar | ((A) B C) | A |
Cadr | (A B C) | B — CDR затем CAR |
Caddr | (A B C) | C — (дважды CDR) затем CAR |
Cadadr | (A (B C) D) | C — два раза (CDR затем CAR) |
Общий подход к обработке символьных выражений и представлению программ
Приведенные ранее описания и правила записи функций и выражений в этой лекции получат более строгое определение. Начнем с синтаксического обобщения. Представим результаты предыдущей лекции в виде простых БНФ (Формул Бекуса-Наура), позволяющих задать грамматику представления функций и значений в виде системы правил. Каждое правило отдельному понятию сопоставляет ( : : = ) варианты ( | ) его изображения:
Синтаксис данных в Лиспе сводится к правилам представления атомов и S-выражений, включая списки.
атом ::= БУКВА конец_атома
Это правило констатирует, что атомы начинаются с буквы.
конец_атома ::= пусто | БУКВА конец_атома | цифра конец_атома
Это правило констатирует, что после первой литеры в изображении атома могут быть как буквы, так и цифры.
В Лиспе атомы — это мельчайшие частицы. Их разложение по литерам не имеет смысла.
S-выражение ::= атом | (S-выражение . S-выражение) | (S-выражение ... )
Данное правило констатирует, что S-выражения — это или атомы, или узлы из пары S-выражений, или списки из S-выражений. (Три точки означают, что допустимо любое число вхождений предшествующего вида объектов, включая ни одного.)
Согласно такому правилу "()" есть допустимое S-выражение. Оно в языке Лисп по соглашению эквивалентно атому Nil.
Базовая система представления данных — точечная нотация, хотя на практике запись в виде списков удобнее. Любой список можно представить точечной нотацией:
() = Nil (a . Nil) = (a) - - - (a1 . ( ... (aK . Nil) ... )) = (a1 ... aK)
Такая единая структура данных оказалась вполне достаточной для представления сколь угодно сложных программ. Дальнейшее определение языка Лисп можно рассматривать как восходящий процесс генерации семантического каркаса, по ключевым позициям которого распределены семантические действия по обработке программ.
Другие правила представления данных нужны лишь при расширении и специализации лексики языка (числа, строки, имена особого вида и т.п.). Они не влияют ни на общий синтаксис языка, ни на строй его понятий, а лишь характеризуют разнообразие сферы его конкретных приложений.
Синтаксис программ является конкретизацией синтаксиса данных, а именно — выделением из класса S-выражений подкласса вычислимых выражений (форм), т.е. данных, имеющих смысл как выражения языка и приспособленных к вычислению. Внешне это выглядит как объявление объектов, заранее известных в языке, и представление разных форм, вычисление которых обладает определенной спецификой.
Выполнение программы устроено как интерпретация данных, представляющих выражения, имеющие значение. Ниже приведены синтаксические правила для обычных конструкций, к которым относятся идентификаторы, переменные, константы, аргументы, формы и функции. (Правила упорядочены по сложности взаимосвязи формул.)
идентификатор ::= атом
Идентификатор — это подкласс атомов, используемых при именовании неоднократно используемых объектов программы — функций и переменных. Предполагается, что идентифицируемые объекты размещаются в памяти так, что по идентификатору их можно найти.
Понятие "идентификатор" выделено для того, чтобы по мере развития определения атома не требовалось на все виды атомов искусственно распространять семантику вычислений. (Например, у Бекуса в его знаменитой статье про "бутылочное горлышко" рассматриваются числа как представление операций доступа [20].)
форма ::= константа | переменная | (функция аргумент ... ) | (COND (форма форма) (форма форма) ... )
константа ::= (QUOTE S-выражение) | 'S-выражение
переменная ::= идентификатор
Переменная — это подкласс идентификаторов, которым сопоставлено многократно используемое значение, ранее вычисленное в подходящем контексте. Подразумевается, что одна и та же переменная в разных контекстах может иметь разные значения.
Таким образом, класс форм — это объединение класса переменных и подкласса списков, начинающихся с QUOTE, COND или с представления некоторой функции.
аргумент ::= форма
Форма — это выражение, которое может быть вычислено. Форма, представляющая собой константу, выдает эту константу как свое значение.
В таком случае нет необходимости в вычислениях, независимо от вида константы. Константные значения могут быть любой сложности, включая вычислимые выражения. Чтобы избежать двусмысленности, предлагается константы изображать как результат специальной функции QUOTE, блокирующей вычисление. Представление констант с помощью QUOTE устанавливает границу, далее которой вычисление не идет. Использование апострофа "'" — просто сокращенное обозначение для удобства набора внешних форм. Константные значения аргументов характерны при тестировании и демонстрации программ.
Если форма представляет собой переменную, то ее значением должно быть S-выражение, связанное с этой переменной до момента вычисления формы. (Динамическое связывание, в отличие от традиционного правила, требующего связывания к моменту описания формы, т.е. статическое связывание.)
Третья ветвь определения гласит, что можно написать функцию, затем перечислить ее аргументы, и все это как общий список заключить в скобки.
Аргументы представляются формами. Это означает, что допустимы композиции функций. Обычно аргументы вычисляются в порядке вхождения в список аргументов. Позиция "аргумент" выделена для того, чтобы было удобно в дальнейшем локализовывать разные схемы обработки аргументов в зависимости от категории функций. Аргументом может быть любая форма, но метод вычисления аргументов может варьироваться. Функция может не только учитывать тип обрабатываемого данного, но и управлять временем обработки данных, принимать решения по глубине и полноте анализа данных, обеспечивать продолжение счета при исключительных ситуациях и т.п.
Последняя ветвь определяет формат условного выражения. Согласно этому формату условное выражение строится из размещенных в двухэлементном списке синтаксически различимых позиций для пропозициональных термов и обычных форм. Двухэлементные списки из определения условного выражения рассматриваются как представление предиката и соответствующего ему S-выражения. Значение условного выражения определяется перебором предикатов по порядку, пока не найдется форма, значение которой отлично от Nil, что означает логическое значение "истина".
Строго говоря, такая форма должна быть найдена непременно. Тогда вычисляется S-выражение, размещенное вторым элементом этого же двухэлементного списка. Остальные предикаты и формы условного выражения не вычисляют (логика Мак-Карти), их формальная корректность или определенность не влияют на существование результата.
Разница между пропозициональными и обычными формами заключается лишь в трактовке их результатов. Любая форма может играть роль предиката.
функция ::= название | (LAMBDA список_переменных форма) | (LABEL название функция)
список_переменных ::= (переменная ... )
название ::= идентификатор
Название — это подкласс идентификаторов, определение которых хранится в памяти, но оно может не подвергаться влиянию контекста вычислений.
Таким образом, класс функций — это объединение класса назва-ний и подкласса трехэлементных списков, начинающихся с LAMBDA или LABEL.
Функция может быть представлена просто именем. В таком случае ее смысл должен быть заранее известен. Функция может быть введена с помощью лямбда-выражения, устанавливающего соответствие между аргументами функции и связанными переменными, упоминаемыми в теле ее определения (в определяющей ее форме). Форма из определения функции может включать переменные, не включенные в лямбда-список, — так называемые свободные переменные. Их значения должны устанавливаться на более внешнем уровне. Если функция рекурсивна, то следует объявить ее имя с помощью специальной функции
LABEL. (Используемая в примерах DEFUN, по существу, совмещает эффекты LABEL и LAMBDA.)
форма ::= переменная | (QUOTE S-выражение) | (COND (форма форма) ... (форма форма)) | (функция аргумент ... )
аргумент ::= форма
переменная ::= идентификатор
функция ::= название | (LAMBDA список_переменных форма) | (LABEL название функция)
список_переменных ::= (переменная ... ) название ::= идентификатор
идентификатор ::= атом S-выражение ::= атом | (S-выражение . S-выражение) | (S-выражение ...)
атом ::= БУКВА конец_атома
конец_атома ::= пусто | БУКВА конец_атома | цифра конец_атома
Определение универсальной функции
Универсальная функция EVAL, которую предстоит определить, должна удовлетворять следующему условию: если представленная аргументом форма сводится к функции, имеющей значение на списке аргументов этой же формы, то данное значение и является результатом функции
eval.
(eval '(fn arg1 ... argK)) ; = результат применения fn к аргументам arg1, ..., argK.
Явное определение такой функции позволяет достичь четкости механизмов обработки Лисп-программ.
(eval '((LAMBDA (x y) (CONS (CAR x) y)) '(A B) '(C D) )) ; = (A C D)
Вводим две важные функции
EVAL и
APPLY для обработки форм и обращения к функциям, соответственно. Каждая из этих функций использует ассоциативный список для хранения связанных имен — значений переменных и определений функций.
Сначала этот список пуст.
Вернемся к синтаксической сводке вычислимых форм.
форма ::= переменная | (QUOTE S-выражение) | (COND (форма форма) ... (форма форма)) | (функция аргумент ...)
аргумент ::= форма
переменная ::= идентификатор
функция ::= название | (LAMBDA список_переменных форма) | (LABEL название функция) список_переменных ::= (переменная ... )
название ::= идентификатор
идентификатор ::= атом
S-выражение ::= атом | (S-выражение . S-выражение) | (S-выражение ...)
Ветвям этой сводки будут соответствовать ветви универсальной функции:
Поэтому понадобится вспомогательная функция
APPLY для обработки обращений к функциям. Кроме того работа с идентификаторами использует ассоциативный список для хранения связанных имен - значений переменных и определений функций.
(DEFUN eval (e) (eval-a e '((Nil . Nil)(T . T))))
Вспомогательная функция EVAL-A понадобилась, чтобы для EVAL завести накапливающий параметр — ассоциативный список , в котором будут храниться связи между переменными с их значениями и названиями функций с их определениями. Здесь его значение ((Nil . Nil)(T . T)) обеспечивает, что атомы NIL и T обозначают сами себя.
(DEFUN eval(e a) (COND ((atom e) (cdr(assoc e a)) ) ((eq (car e) 'QUOTE) (cadr e)) ((eq(car e) 'COND) (evcon(cdr e) a)) ( T (apply (car e) (evlis(cdr e) a) a) ) ) )
(defun apply (fn x a) (COND ((atom fn)
(COND ((eq fn 'CAR) (caar x)) ((eq fn 'CDR) (cdar x)) ((eq fn 'CONS) (cons(car x)(cadr x)) ) ((eq fn 'ATOM) (atom(car x)) ) ((eq fn 'EQ) (eq(car x)(cadr x)) ) (T (apply (eval fn a) x a)) ) )
((eq(car fn)'LAMBDA) (eval-a (caddr fn) (pairlis (cadr fn) x a) )) ((eq (car fn) 'LABEL) (apply (caddr fn) x (cons (cons (cadr fn)(caddr fn)) a) ) ) ) )
ASSOC и PAIRLIS уже определены ранее.
(DEFUN evcon (c a) (COND ((eval (caar c) a) (eval (cadar c) a) ) ( T (evcon (cdr c) a) ) ) )
( Не допускается отсутствие истинного предиката, т.е. пустого C.)
(DEFUN evlis (m a) (COND ((null m) Nil ) ( T (cons (eval (car m) a) (evlis(cdr m) a) ) ) ) )
При
(DEFUN eval (e) (eval-a e ObList ))
определения функций могут накапливаться в системной переменной ObList, то есть работать как глобальные определения. ObList обязательно должна содержать глобальное определение встроенной константы "Nil", можно и сразу разместить в ней "T".
Поясним ряд пунктов этих определений.
Первый аргумент EVAL — форма. Если она — атом, то этот атом может быть только именем переменной, а значение переменной должно уже находиться в ассоциативном списке.
Если CAR от формы — QUOTE, то она представляет собой константу, значение которой выделяется как
CADR от нее самой.
Если CAR от формы — COND, то форма — условное выражение. Вводим вспомогательную функцию
EVCON (определение ее будет дано ниже), которая обеспечивает вычисление предикатов (пропозициональных термов) по порядку и выбор формы, соответствующей первому предикату, принимающему значение "истина". Эта форма передается EVAL для дальнейших вычислений.
Все остальные случаи рассматриваются как список из функции с аргументами.
Вспомогательная функция
EVLIS обеспечивает вычисление аргументов, затем представление функции и список вычисленных значений аргументов передаются функции APPLY.
Первый аргумент APPLY — функция. Если она — атом, то существует две возможности. Атом может представлять одну из элементарных функций
(CAR CDR CONS ATOM EQ). В таком случае соответствующая ветвь вычисляет значение этой функции на заданных аргументах. В противном случае, этот атом — имя функции или название ранее заданного определения, которое можно найти в ассоциативном списке , подобно вычислению переменной.
Если функция начинается с LAMBDA, то ее аргументы попарно соединяются со связанными переменными, а тело определения (форма из лямбда-выражения) передается как аргумент функции EVAL-A для дальнейшей обработки.
Если функция начинается с LABEL, то ее название и определение соединяются в пару, и полученная пара размещается в ассоциативном списке, чтобы имя функции стало определенным при дальнейших вычислениях. Они произойдут как рекурсивный вызов APPLY, которая вместо имени функции теперь работает с ее определением при более полном ассоциативном списке — в нем уже размещено определение имени функции. Поскольку определение размещается "наверху" стека, оно становится доступным для всех последующих переопределений, то есть работает как локальный объект. Глобальные объекты, которые обеспечиваются псевдо-функцией DEFUN, устроены немного иначе, что будет рассмотрено в следующей лекции.
Определение универсальной функции является важным шагом, показывающим одновременно и механизмы реализации функциональных языков, и технику функционального программирования на любом языке. Пока еще не описаны многие другие особенности языка Лисп и функционального программирования, которые будут рассмотрены позднее. Но все они будут увязаны в единую картину, основа которой согласуется с этим определением.
В строгой теории аппликативного программирования все функции следует определять всякий раз, когда они используются. На практике это неудобно. Реальные системы имеют большой запас встроенных функций (более тысячи в Clisp-е), известных языку, и возможность присоединения такого количества новых функций, какое понадобится. Во многих реализациях Лиспа все элементарные функции вырабатывают результат и на списках, и на атомах, но его смысл зависит от системных решений, что может создавать трудности при переносе программ на другие системы.
Базисный предикат EQ всегда имеет значение, но смысл его на неатомарных аргументах будет более ясен после знакомства со структурами данных, используемыми для представления списков в машине.В чистом языке Лисп базисные функции CAR и CDR не определены для атомарных аргументов. Такие функции, имеющие осмысленный результат не на всех значениях естественной области определения, называют частичными. Отладка и применение частичных функций требует большего контроля, чем работа с тотальными, всюду определенными функциями. Во многих реализациях функциональных языков программирования все функции всегда вырабатывают значение. При необходимости каждый существенный класс объектов пополняется значением класса ERROR, символизирующим исключительные ситуации.Для функциональных языков характерно большое разнообразие условных форм, конструкций выбора, ветвлений и циклов, практически без ограничений на их комбинирование. Форма COND выбрана для начального знакомства как наиболее общая. За редким исключением в Лиспе нет необходимости писать в условных выражениях (QUOTE T) или (QUOTE NIL). Вместо них используются встроенные константы
T и Nil, соответственно.В реальных системах функционального программирования обычно поддерживается работа с целыми, дробными и вещественными числами в предельно широком диапазоне, а также работа с битовыми и текстовыми строками. Такие данные, как и атомы, являются минимальными объектами при обработке информации, но отличаются от атомов тем, что их смысл задан непосредственно их собственным представлением. Их понимание не требует ассоциаций или связывания. Поэтому и константы такого вида не нуждаются в префиксе в виде апострофа.
Приведенное выше самоопределение Лисп-интерпретации является концептуальным минимумом, обеспечивающим постепенность восприятия более сложных особенностей специфики функционального программирования, а также методов реализации языков и систем программирования, которые будут иллюстрироваться в дальнейшем. Они будут введены как расширения или уточнения чистого определения универсальной функции.
Основные методы обработки списков
Следующие функции полезны, когда рассматриваются лишь списки.
APPEND — функция двух аргументов x и y, сцепляющая два списка в один.
(DEFUN append (x y) (COND ((null x) y) ((QUOTE T) (CONS (CAR x) (append (CDR x) y) ) ) ) ) (append '(A B) '(C D E)) ; = (A B C D E)
MEMBER — функция двух аргументов x и y, выясняющая, встречается ли S-выражение
x среди элементов списка y.
(DEFUN member (x y) (COND ((null y) (QUOTE Nil) ) ((equal x (CAR y)) (QUOTE T) ) ((QUOTE T) (member x (CDR y)) ) ) ) (member '(a) '(b (a) d)) ; = T (member 'a '(b (a) d)) ; = NIL
PAIRLIS — функция аргументов x, y, al строит список пар соответствующих элементов из списков x и y и присоединяет их к списку al. Полученный список пар, похожий на таблицу с двумя столбцами, называется ассоциативным списком или ассоциативной таблицей. Такой список может использоваться для связывания имен переменных и функций при организации вычислений интерпретатором.
(DEFUN pairlis (x y al) (COND ((null x) al) ((QUOTE T) (CONS (CONS (CAR x)(CAR Y) ) (pairlis (CDR x)(CDR y)al) ) ) ) ) (pairlis '(A B C) '(u t v) '((D . y)(E . y)) ) ; = ((A . u)(B . t)(C . v) (D . y)(E . y))
ASSOC — функция двух аргументов, x и al. Если al — ассоциативный список, подобный тому, что формирует функция pairlis, то assoc выбирает из него первую пару, начинающуюся с x. Таким образом, это функция поиска определения или значения по таблице, реализованной в форме ассоциативного списка .
(DEFUN assoc (x al) (COND ((equal x (CAAR al)) (CAR al) ) ((QUOTE T) (assoc x (CDR al)) ) ) )
Частичная функция — рассчитана на наличие ассоциации.
(assoc 'B '((A . (m n)) (B . (CAR x)) (C . w) (B . (QUOTE T)) ) ) ; = (B . (CAR x))
SUBLIS — функция двух аргументов al и y, предполагается, что первый из аргументов AL устроен как ассоциативный список вида ((u1 . v1) ... (uK . vK)), где u есть атомы, а второй аргумент Y — любое S-выражение. Действие sublis заключается в обработке Y, такой, что вхождения переменных
Ui, связанные в ассоциативном списке со значениями Vi, заменяются на эти значения.
Другими словами в S-выражении Y вхождения переменных U заменяются на соответствующие им V из списка пар AL. Вводим вспомогательную функцию
SUB2, обрабатывающую атомарные S-выражения, а затем — полное определение SUBLIS:
(DEFUN sub2 (al z) (COND ((null al) z) ((equal (CAAR al) z) (CDAR al) ) ((QUOTE T) (sub2(CDR al)z) ) ) )
(DEFUN sublis (al y) (COND ((ATOM y) (sub2 al y)) ((QUOTE T)(CONS (sublis al (CAR y)) (sublis al (CDR y)) ) ) ) )
(sublis '((x . Шекспир) (y . (Ромео и Джульетта)) ) '(x написал трагедию y) ) ; = (Шекспир написал трагедию (Ромео и Джульетта))
Пример 3.1.
INSERT — вставка
z перед вхождением ключа
x в список al.
(DEFUN insert (al x z) (COND ((null al) Nil) ((equal (CAR al) x) (CONS z al) ) ((QUOTE T) (CONS (CAR al) (insert (CDR al) x z) )) ) ) (insert '(a b c) 'b 's) = (a s b c)
ASSIGN — модель присваивания переменным, хранящим значения в ассоциативном списке . Замена связанного с данной переменной в первой паре значения на новое заданное значение. Если пары не было вообще, то новую пару из переменной и ее значения помещаем в конец а-списка, чтобы она могла работать как глобальная.
(DEFUN assign (x v al) (COND ((Null al) (CONS(CONS x v) Nil ) ) ((equal x (CAAR al)) (CONS(CONS x v) (CDR al)) ) ((QUOTE T) (CONS (CAR al) (assign x v (CDR al)) )) ) )
(assign 'a 111 '((a . 1)(b . 2)(a . 3))) ; = ((a . 111)(b . 2)(a . 3))
(assign 'a 111 '((c . 1)(b . 2)(a . 3))) ; = ((c . 1)(b . 2)(a . 111))
(assign 'a 111 '((c . 1)(d . 3))) ; = ((c . 1)(d . 3) (a . 111))
REVERSE — обращение списка — два варианта, второй с накапливающим параметром и вспомогательной функцией:
(DEFUN reverse (m) (COND ((null m) NIL) (T (append(reverse(CDR m)) (list(CAR m)) )) ) )
(DEFUN reverse (m) (rev m Nil)) (DEFUN rev (m n) (COND ((null m)N) (T (rev(CDR m) (CONS (CAR m) n)) ) ) )
Предикаты и истинность в Лиспе
Хотя формальное правило записи программ вычислений в виде S-выражения предписывает, что константа Т — это (QUOTE T), было оговорено, что в системе всегда пишется Т. Кроме того, Nil оказался удобнее, чем атом F, встречавшийся в начальных предложениях по Лиспу аналог значения FALSE. Программист может либо принять это правило на веру, либо изучить следующие уточнения.
В Лисп есть два атомных символа, которые представляют истину и ложь, соответственно. Эти два атома — T и NIL. Данные символы — действительные значения всех предикатов в системе. Главная причина в удобстве кодирования. Во многих случаях достаточно отличать произвольное значение от пустого списка. Если атомы T и F имеют значение T и NIL, соответственно, то символы T и F в качестве константных предикатов могут работать, потому что:
(eval-a T '((Nil . Nil)(T . T) (F . NIL))) ; = T (eval-a NIL'((Nil . Nil)(T . T) (F . NIL))) ; = NIL (eval-a F '((Nil . Nil)(T . T) (F . NIL))) ; = NIL
Формы (QUOTE T) и (QUOTE NIL) будут также работать, потому что:
(eval (QUOTE T) ) ; = T (eval (QUOTE NIL) ) ; = NIL
Но
(eval (QUOTE F)NIL) ; = F
Это неправильно, отлично от NIL, и поэтому (QUOTE F) не будет работать как представление ложного значения в системе.
Заметим, что
(eval T ) ; = T (eval NIL ) ; = NIL
будет работать в силу причин, которые объясняются в лекции 6.
Формального различия между функцией и предикатом в Лиспе не существует. Предикат может быть определен как функция со значениями либо T либо NIL. Это верно для всех предикатов системы. Можно использовать форму, не являющуюся предикатом там, где требуется предикат: предикатная позиция условного выражения или аргумент логической операции. Семантически любое S-выражение, отличного от NIL, будет рассматриваться в таком случае как истинное. Первое следствие из этого — предикат Null и логическое отрицание Not идентичны. Второе — то, что (QUOTE T) или (QUOTE Х) практически эквивалентны Т как константные предикаты.
Предикат EQ ведет себя следующим образом:
Если его аргументы различны, значением EQ является NIL.Если оба его аргументы являются одним и тем же атомом, то значение — Т.Если значения одинаковы, но не атомы, то его значение T или NIL в зависимости от того, идентично ли представление аргументов в памяти.
Значение EQ всегда T или NIL. Оно никогда не бывает не определено, даже если аргументы неправильные.
Универсальная функция — это джин, выпущенный из бутылки, т.к. потенциал такой функции ограничен лишь способностями нашего воображения. Пока рассмотрены лишь простейшие, самые очевидные следствия из возможности явно применять и уточнять механизмы символьного представления и определения функций, такие как использование накапливающих параметров, связывание обозначений по схеме знак-смысл в ассоциативном списке как имен переменных со значениями, так и названий функций с определениями, а также применение вспомогательных функций для достижения прозрачности определений. Эти возможности имеют место в любом языке высокого уровня. Но попутно выполнено достаточно строгое построение совершенно формальной математической системы, называемой "Элементарный ЛИСП". Составляющие этой формальной системы следующие:
Множество символов, называемых S-выражениями.Система функциональных обозначений для основных понятий, необходимых при программировании обработки S-выражений.Формальное представление функциональных обозначений в виде S-выражений.Универсальная функция (записанная в виде S-выражения), интерпретирующая обращение произвольной функции, записанной как S-выражение, к ее аргументам.Система базовых функций, обеспечивающих техническую поддержку обработки S-выражений, и специальных функций, обеспечивающих управление вычислениями.
Более интересные и не столь очевидные следствия возникают при расширении этой формальной системы, что и будет продемонстрировано в следующих лекциях.

x написал трагедию y)
|
(DEFUN sub2 (al z) (COND ((null al) z) ((equal (CAAR al) z) (CDAR al) ) ((QUOTE T) (sub2(CDR al)z) ) ) ) (DEFUN sublis (al y) (COND ((ATOM y) (sub2 al y)) ((QUOTE T)(CONS (sublis al (CAR y)) (sublis al (CDR y)) ) ) ) ) (sublis '((x . Шекспир) (y . (Ромео и Джульетта)) ) '( x написал трагедию y) ) ; = (Шекспир написал трагедию (Ромео и Джульетта)) |
| Пример 3.1. |
| Закрыть окно |
Универсальная функция
Интерпретация или универсальная функция — это функция, которая может вычислять значение любой формы, включая формы, сводимые к вычислению произвольной заданной функции, применяемой к аргументам, представленным в этой же форме, по доступному описанию данной функции. (Конечно, если функция, которой предстоит интерпретироваться, имеет бесконечную рекурсию, интерпретация будет повторяться бесконечно.)
Определим универсальную функцию eval от аргумента expr — выражения, являющегося произвольной вычислимой формой языка Лисп.
Универсальная функция должна предусматривать основные виды вычисляемых форм, задающих значения аргументов, а также представления функций, в соответствии со сводом приведенных выше правил языка. При интерпретации выражений учитывается следующее:
атомарное выражение обычно понимается как переменная. Для него следует найти связанное с ним значение. Например, могут быть переменные вида x, elem, смысл которых зависит от контекста, в котором они вычисляются;
константы представленные как аргументы функции QUOTE, можно просто извлечь из списка ее аргументов. Например, значением константы (QUOTE T) является атом T, обычно символизирующий значение "истина";
условное выражение требует специального алгоритма для перебора предикатов и выбора нужной ветви. Например, интерпретация условного выражения
(COND ((ATOM x) x) ((QUOTE T) (first (CAR x)) ) )
должна обеспечивать выбор ветви в зависимости от атомарности значения аргумента. Семантика чистого Лиспа не определяет значение условного выражения при отсутствии предиката со значением "истина". Но во многих реализациях и диалектах Лиспа такая ситуация не рассматривается как ошибка, а значением считается Nil. Иногда это придает условным выражениям лаконичность; остальные формы выражений рассматриваются по общей схеме как список из функции и ее аргументов. Обычно аргументы вычисляются, а затем вычисленные значения передаются функции для интерпретации ее определения. Так обеспечивается возможность писать композиции функций.
Например, в выражении (first (CAR x)) внутренняя функция CAR сначала получит в качестве своего аргумента значение переменной x, а потом свой результат передаст как аргумент более внешней функции first;если функция представлена своим названием, то среди названий различаются имена встроенных функций, такие как CAR, CDR, CONS и т.п., и имена функций, введенных в программе, например first. Для встроенных функций интерпретация сама "знает", как найти их значение по заданным аргументам, а для введенных в программе функций — использует их определение, которое находит по имени;если функция использует лямбда-конструктор, то прежде чем его применять, понадобится связывать переменные из лямбда-списка со значениями аргументов. Функция, использующая лямбда-выражение,
(LAMBDA (x) (COND ((ATOM x) x) ((QUOTE T) (first (CAR x)) ) ) )
зависит от одного аргумента, значение которого должно быть связано с переменной x. В определении используется свободная функциональная переменная first, которая должна быть определена в более внешнем контексте;если представление функции начинается с LABEL, то понадобится сохранить имя функции с соответствующим ее определением так, чтобы корректно выполнялись рекурсивные вызовы функции. Например, предыдущее LAMBDA-определение безымянной функции становится рекурсивным, если его сделать вторым аргументом специальной функции LABEL, первый аргумент которой — fisrt, имя новой функции.
(LABEL first (LAMBDA (x) (COND ((ATOM x) x) ((QUOTE T) (first (CAR x)) ) ) ) )
Таким образом, интерпретация функций осуществляется как взаимодействие четырех подсистем:
обработка структур данных (cons, car, cdr, atom, eq);конструирование функциональных объектов (lambda, label);идентификация объектов (имена переменных и названия функций);управление логикой вычислений и границей вычислимости (композиции, quote, cond, eval).
В большинстве языков программирования аналоги первых двух подсистем нацелены на обработку элементарных данных и конструирование составных значений, кроме того, иначе установлены границы между подсистемами.
Прежде чем дать определение универсальной функции, опишем ряд дополнительных функций, полезных при обработке S-выражений. Некоторые из них пригодятся при определении интерпретатора.
Начнем с общих методов обработки S-выражений.
AMONG — проверка, входит ли заданный атом в данное S-выражение.
(DEFUN among (x y) (COND ((ATOM y) (EQ x y)) ((among x (CAR y)) (QUOTE T)) ((QUOTE T) (among x (CDR y) )) ) ) (among 'A '(C (A B))) ; = T (among 'A '(C D B)) ; = NIL
Символ ";" - начало примечания (до конца строки).
EQUAL — предикат, проверяющий равенство двух S-выражений. Его значение "истина" для идентичных аргументов и "ложь" для различных. (Элементарный предикат EQ определен только для атомов.) Определение EQUAL иллюстрирует условное выражение внутри условного выражения (двухуровневое условное выражение и двунаправленная рекурсия).
(DEFUN equal (x y) (COND ((ATOM x) (COND ((ATOM y) (EQ x y)) ((QUOTE T) (QUOTE NIL)) ) ) ((equal (CAR x)(CAR y)) (equal (CDR x)(CDR y)) )
((QUOTE T) (QUOTE NIL) ) ) ) (equal '(A (B)) '(A (B))) ; = T (equal '(A B) '(A . B)) ; = NIL
SUBST — функция трех аргументов x, y, z, строящая результат замены S-выражением x всех вхождений y в S-выражение z.
(DEFUN subst (x y z) (COND ((equal y z) x) ((ATOM z) z) ((QUOTE T)(CONS (subst x y (CAR z)) (subst x y (CDR z)) ) ) ) ) (subst '(x . A) 'B '((A . B) . C)) ; = ((A . (x . A)) . C)
Использование equal в этом определении позволяет осуществлять подстановку и в более сложных случаях. Например, для редукции совпадающих хвостов подсписков:
(subst 'x '(B C D) '((A B C D)(E B C D)(F B C D))) ; = ((A . x) (E . x) (F . x))
NULL — предикат, отличающий пустой список от остальных S-выражений. Позволяет выяснять, когда список исчерпан. Принимает значение "истина" тогда и только тогда, когда его аргумент — Nil.
(DEFUN null (x) (COND ((EQ x (QUOTE Nil)) (QUOTE T)) ((QUOTE T) (QUOTE Nil)) ) )
При необходимости можно компоненты точечной пары разместить в двухэлементном списке функцией PAIR_TO_LIST, и наоборот, из первых двух элементов списка построить в точечную пару функцией LIST_TO_PAIR.
(DEFUN pair_to_list (x) (CONS (CAR x) (CONS (CDR x) Nil)) ) (pair_to_list '(A B)) ; = (A B)
(DEFUN list_to_pair (x) (CONS (CAR x) (CADR x)) ) (list_to_pair '(A B C)) ; = (A . B)
По этим определениям видно, что списочная запись строится большим числом CONS, т.е. на нее расходуется больше памяти.
Безымянные функции
Определения в примерах 4.4 и 4.5 не вполне удобны по следующим причинам:
в определениях целевых функций duble и sqware встречаются имена специально определенных вспомогательных функций;формально эти функции независимы, значит, программист должен отвечать за их наличие при использовании целевых функций на протяжении всего жизненного цикла программы, что трудно гарантировать;вероятно, имя вспомогательной функции будет использоваться только один раз - в определении целевой функции.
С одной стороны, последнее утверждение противоречит пониманию смысла именования как техники, обеспечивающей неоднократность применения поименованного объекта. С другой стороны, придумывать подходящие, долго сохраняющие понятность и соответствие цели, имена - задача нетривиальная.
Учитывая это, было бы удобнее вспомогательные определения вкладывать непосредственно в определения целевых функций и обходиться при этом вообще без имен. Конструктор функций lambda обеспечивает такой стиль построения определений. Этот конструктор любое выражение expr превращает в функцию с заданным списком аргументов (x1. .. xK) в форме так называемых lambda-выражений:
(lambda (x1 ... xK) expr)
Имени такая функций не имеет, поэтому может быть применена лишь непосредственно. DEFUN использует данный конструктор, но требует дать функциям имена.
Определение функций duble и sqware из примеров 4.4 и 4.5 без использования имен и вспомогательных функций:
(defun sqware (xl) (map-el #' (lambda (x) (* x x)) xl))
(defun duble (xl) (map-el #' (lambda (x) (cons x x)) xl))
Пример 4.9.
Любую систему взаимосвязанных функций можно преобразовать к одной функции, используя вызовы безымянных функций.
Числа и мультиоперации
Любую информацию можно представить в виде символьных выражений. В качестве основных видов символьных выражений выбраны списки и атомы.
Атом - неделимое данное, представляющее информацию произвольной природы.
Во многих случаях знание природы информации дает более четкое понимание особенностей изучаемых механизмов. Программирование работы с числами и строками - привычная, хорошо освоенная область информационной обработки, удобная для оценки преимуществ использования функционалов. Опуская технические подробности, просто отметим, что числа и строки рассматриваются как самоопределимые атомы, смысл которых не требует никакого ассоциирования, он понятен просто по виду записи.
Например, натуральные числа записываются без особенностей и могут быть почти произвольной длины:
1 -123 9876543210000000000000123456789
Можно работать с дробными и вещественными числами:
2/3 3.1415926
Строки заключаются в обычные двойные кавычки: "строка любой длины из произвольных символов, включая все что угодно".
Список - составное данное, первый элемент которого может рассматриваться как функция, применяемая к остальным элементам, также представленным как символьные выражения. Это относится и к операциям над числами и строками:
(+ 1 2 3 4 5 6) = 21 (- 12 6 3) = 3 (/ 3 5) = 3/5 (1+ 3) = 4
Большинство операций над числами при префиксной записи естественно рассматривать как мультиоперации от произвольного числа аргументов.
(string-equal "строка 1" "строка1") = Nil (ATOM "a+b-c") = T (char "стр1" 4 ) = "1"
Со строками при необходимости можно работать посимвольно, хотя они рассматриваются как атомы.
Любой список можно превратить в константу, поставив перед ним <'> апостроф. Это эквивалентно записи со специальной функцией QUOTE. Для чисел и строк в этом нет необходимости, но это не запрещено.
'1 = 1 '"abc" = "abc"
Можно строить композиции функций. Ветвления представлены как результат специальной функции COND, использующей отличие от Nil в качестве значения <истина>. Числа и строки таким образом оказываются допустимыми представлениями значения <истина>. Отказ от барьера между представлениями функций и значений дает возможность использовать символьные выражения как для изображения заданных значений, включая любые структуры над числами и строками, так и для определения функций, обрабатывающих любые данные. (Напоминаем, что определение функции - данное.) Функционалы - это функции, которые используют в качестве аргументов или результатов другие функции. При построении функционалов переменные могут играть роль имен функций, определения которых находятся во внешних формулах, использующих функционалы.
Для самостоятельного решения
Можно предложить следующие задачи на применение функционалов:
1) Напишите определение функционала F-ALL, выясняющего, все ли элементы множества Set удовлетворяют заданному предикату Pred.
(defun f-all (Pred Set ) . . . )
2) Напишите определение функционала F-ex, выясняющего, найдется ли в множестве Set элемент, удовлетворяющий заданному предикату Pred.
(defun f-ex (Pred Set ) . . . )
3) Пусть программа представляет собой набор списков, содержащих имя команды и произвольное число операндов. Имя расположено первым в списке. Напишите определение функционала, удобного для выдачи списка операндов, встречающихся в программе, а также для выдачи отдельных интегральных характеристик, таких как суммарное число всех операндов, максимальное число операндов в команде и т.п.
4) Напишите универсальный фильтр, позволяющий из произвольного списка выделять при необходимости атомы, числа, строки или списки, начинающиеся с заданного атома, и т.д.
5) Пусть клетки доски типа шахматной пронумерованы по горизонтали символами, а по вертикали числами. И то, и другое перечислено в отдельных списках по порядку. Напишите функцию перечисления координат всех клеток доски, соответствующей размерам списков.
6) При анализе труднодоступных данных требуется всю потенциально полезную информацию выяснять сразу, <в одно касание>. Напишите модель такого стиля работы на примере покомпонетной обработки двух списков чисел. Роль полезной информации могут играть значения любых бинарных операций, таких как +, *, -, /, max, min и т.п.
7) Пусть программа представляет собой набор списков, содержащих имя команды и не более двух операндов. Имя расположено в списке первым. Напишите определение функционала, удобного для выдачи по мере необходимости перечня команд, или перечня первых операндов, или вторых операндов и т.п.
Подготовьте определения вспомогательных функций на все эти случаи.
8) Список содержит ежедневные сведения о количестве осадков, выпавших за весьма длительный период. Напишите функционал, позволяющий по этому списку оперативно выяснять различные сведения, наподобие:
суммарный объем осадков;максимальное количество осадков в день;минимальное количество осадков в день;максимальная разница в количестве осадков в соседние дни.
9) Задача повышенной сложности (с решением).
Лексикон ***)
Условие задачи: Группа специалистов договорилась подготовить лексикон программирования для электронной публикации. Было решено, что надо добиться <правильности> определения понятий программирования, а именно не допускать цепочек понятий прямо или косвенно определяемых через себя. Кроме того, следует обеспечить полноту комплекта определений, т.е. всякое включенное в лексикон понятие должно иметь определение.
Напишите программу, помогающую по ходу разработки лексикона отслеживать его <правильность> и полноту.
Входные данные:
(( имя_понятия объяснение ) ... ) - двухуровневый список, в котором имя_понятия - атом, обозначающий определяемое понятие, объяснение - последовательность строк и/или атомов, строки не требуют определения, а атомы должны получить определения в процессе разработки, но, возможно, еще не все слова удалось объяснить.
Выходные данные:
Словарь правилен или Есть неправильные цепочки имя_понятия1 ... имя_понятияN |___________________|______ начала неправильных цепочек и/или Есть неопределенные понятия имя_понятия1 ... имя понятияN |___________________|_______ имена неопределенных понятий (слова перечисляются в порядке включения в словарь.)
Пример ввода:
(( автокод язык_программирования <используется для создания> операционная_система <и> транслятор) ( язык_программирования <задается множеством правил для написания> программ) ( операционная_система <комплекс> программа <управляющих решением задач на имеющемся оборудовании>) ( транслятор <компилирующая> программа) ( программа <описание> алгоритм <решения задачи на соответствующем языке>) ( алгоритм <точно определенное правило действий>) )
Уточнения:
Может ли объяснение быть пустым? - Да.Может ли быть много объяснений для одного имени? - Да.Могут ли быть идентичные объяснения? - Да.Может ли одно слово входить в объяснение неоднократно? - Да.Предполагается ли одновременная диагностика и циклов, и неопределенностей? - Да.При выводе результата неопределенные имена надо вывести все.
Пример теста:
(( а-к яп <используется для создания> ос <и> сп) ( яп <задается множеством правил для написания> пр) ( ос <комплекс> пр <управляющих решением задач на имеющемся оборудовании>) ( сп <компилирующая> пр) ( пр <описание> алг <решения задачи на соответствующем языке>) ( алг <точно определенное правило действий>) )
'(( а-к яп ос сп) ( яп пр) ( ос пр) ( сп пр) ( пр алг) ( алг ))
;;=== Лексикон****) - проверка корректности == ;; Предполагается, что из теста уже ;; отфильтрованы строки, ;; т.к. они не влияют на логику анализа корректности
(defun names (vac) (mapcar 'car vac)) ;; определяемые имена - список левых частей
(defun words (vac) (cond ;; используемые имена - список правых частей ((null vac) NIL) (T (union (cdar vac) (words (cdr vac)))) )) (defun undef (vac) (set-difference (words vac) (names vac))) ;; неопределенные имена - список висячих ссылок (defun circle (v) ;; проверка термина на явный цикл (cond ((null (cdr v)) NIL)
((member (car v) (cdr v)) (car v)) (T NIL) ))
(defun circ-v (vac) (mapcar 'circle vac)) ;; список явных циклов с NIL-ами на нециклах
(defun maska (arg xxx) (cond (xxx NIL) (T arg))) ;; выбор, если NIL
(defun del-cir (al xl) (delete NIL (mapcar 'maska al xl))) ;; стирание непомеченных определений, т.е. циклов
(defun skobki (ll) (cond((null ll)nil) ((null (car ll)) (skobki (cdr ll)) ) ((atom (car ll))(cons(car ll) (skobki(cdr ll))) ) (T (union (car ll) (skobki (cdr ll)) )) )) ;; раскрыть скобки на один уровень
(defun onestp (vc)(setq vac vc) ;; однократная постановка всего словаря
(mapcar '(lambda (x) (cons (car x) (skobki (sublis vac (cdr x))) )) vc ))
(defun clean-s (line xl) (cond ((null xl) line) (T (clean-s (delete (car xl) line)(cdr xl) )) ))
(defun clean-u (vc xl) (setq wl xl)
;; стирание заданного списка слов => висячих ссылок
(mapcar '(lambda (xx) (setq x xx) (cons (car x) (clean-s (cdr x) wl) )) vc ))
(defun cvr (vac)(delete NIL (cvr-d (del-cir vac (circ-v vac)) (delete NIL(union (circ-v vac) NIL))))) ;; список всех циклов полного словаря - без ;; висячих ссылок
(defun cvr-d (vc ccl) (prog (vac cl cv dcv cleanv) (setq vac (clean-u vc ccl)) (setq cl ccl)
;; пополнение списка циклов со второго шага LAB (cond ((words vac) (setq cv (circ-v vac)) (setq dcv (delete NIL cv)) (setq cleanv (clean-u (del-cir vac cv) dcv)) (setq vac (onestp cleanv)) (setq cl (append dcv cl)) (go lab) )) (return cl) ))
(defun vac-ok (vac) (prog (vc ul cl) ;; проверка словаря на корректность (setq vc vac) (setq ul (undef vc)) (setq cl (cvr (clean-u vac ul)))
(cond ((eq ul cl) (return(print 'OK)) ) ; = лишь если пусты <> корректность словаря ( CL (print (list 'CIRCLES cl))) )
(cond (UL (return (print (list 'UNDEFINED ul))) ) (T (return (list 'circle cl))) ) ))
*) Символ ";" - начало комментария.
**) На Lisp 1.5 это определение выглядит изящнее, не требует встроенной функции funcall, при отладке примеров на Clisp-е [7]:
(defun map-el (fn xl) (cond (xl (cons (fn (car xl) ) ; применяем первый аргумент как функцию ; к первому элементу второго аргумента (map-el fn (cdr xl) ) ) ) ) )
***) Эта задача была предложена участникам Открытой Всесибирской студеческой олимпиады в 2000 году и оказалась в числе никем не решенных. Многих смутило отсутствие численных ограничений на допустимые данные. При решении задач на Паскале и Си такие ограничения обычно подсказывают выбор структур данных, поэтому отсутствие ограничений было воспринято как риск. Немногочисленные попытки решить задачу привели к отбраковке на минимальных тестах, вызванной тем, что программы не допускали пустой словарь или словарь, выглядящий как перечень терминов без определений. (Впрочем, возможно, это ошибка разработчика тестов. Видимо, первыми должны располагаться тесты на наиболее типичные, естественные случаи.)
****) Решение этой задачи может быть сведено к задаче <Проверка ацикличности графа>.

Функционалы - общее понятие
Рассмотрим технику использования функционалов на упражнениях с числами и покажем, как от простых задач перейти к более сложным.
Для каждого числа из заданного списка получить следующее за ним число и все результаты собрать в список
(defun next (xl) ; Следующие числа*) (cond ; пока список не пуст (xl(cons(1+(car xl)) ; прибавляем 1 к его голове (next(cdr xl)) ; и переходим к остальным, ) ) ) ) ; собирая результаты в список
(next'(1 2 5)) ; = (2 3 6)
Пример 4.1.
Построить список из <голов> элементов списка
(defun 1st (xl) ; "головы" элементов = CAR (cond ; пока список не пуст (xl (cons (caar xl); выбираем CAR от его головы (1st (cdr xl)) ; и переходим к остальным, ) ) ) ) ; собирая результаты в список
(1st'((один два)(one two)(1 2)) ) ; = (один one 1)
Пример 4.2.
Выяснить длины элементов списка
(defun lens (xl) ; Длины элементов (cond ; Пока список не пуст (xl (cons (length (car xl)) ; вычисляем длину его головы (lens (cdr xl)); и переходим к остальным, ) ) ) ) ; собирая результаты в список
(lens'((1 2)()(a b c d)(1(a b c d)3)) ) ; = (2 0 4 3)
Пример 4.3.
Внешние отличия в записи этих трех функций малосущественны, что позволяет ввести более общую функцию map-el, в определении которой имена <car>, <1+> и <length> могут быть заданы как значения параметра fn:
(defun map-el(fn xl) ; Поэлементное преобразование XL ; с помощью функции FN (cond ; Пока XL не пуст (xl(cons(funcall fn (car xl)) ; применяем FN как функцию к голове XL**) (map-el fn (cdr xl)) ; и переходим к остальным, ) ) ) ) ; собирая результаты в список
Эффект функций next, 1st и lens можно получить выражениями:
(map-el #'1+ xl) ; Следующие числа: (map-el #'car xl) ; "головы" элементов = CAR (map-el #'length xl) ; Длины элементов
(map-el #'1+'(1 2 5)) ; = (2 3 6) (map-el #'car'((один два)(one two)(1 2)) ) ; = (один one 1) (map-el #'length'((1 2)()(a b c d)(1(a b c d)3)) ) ; = (2 0 4 3)
соответственно.
Все три примера можно решить с помощью таких определяющих выражений:
(defun next(xl) (map-el #'1+ xl)) ; Очередные числа: (defun 1st(xl) (map-el #'car xl)) ; "головы" элементов = CAR (defun lens(xl) (map-el #'length xl)) ; Длины элементов
Эти определения функций формально эквивалентны ранее приведенным - они сохраняют отношение между аргументами и результатами. Параметром функционала может быть любая вспомогательная функция.
Пусть дана вспомогательная функция sqw, возводящая числа в квадрат
(defun sqw (x)(* x x)) ; Возведение числа в квадрат (sqw 3) ; = 9
Пример 4.4.
Построить список квадратов чисел, используя функцию sqw:
(defun sqware (xl) ; Возведение списка чисел в квадрат (cond ; Пока аргумент не пуст, (xl (cons (sqw (car xl)) ; применяем sqw к его голове (sqware(cdr xl)) ; и переходим к остальным, ) ) ) ) ; собирая результаты в список
(sqware'(1 2 5 7)) ; = (1 4 25 49 )
Можно использовать map-el:
(defun sqware (xl) (map-el #'sqw xl))
Ниже приведено определение функции sqware- без вспомогательной функции, выполняющее умножение непосредственно. Оно влечет за собой двойное вычисление (CAR xl), т.е. такая техника не вполне эффективна:
(defun sqware- (xl) (cond (xl (cons (* (car xl) (car xl) ) ; квадрат головы списка ; голову вычислять приходится дважды (sqware- (cdr xl)) ) ) ) )
Пусть дана вспомогательная функция tuple, превращающая любое данное в пару:
(defun tuple (x) (cons x x)) (tuple 3) (tuple 'a) (tuple '(Ха)) ; = (3 . 3) ; = (a . a) ; = ((Ха) . (Ха)) = ((Ха) Ха) ; - это одно и то же!
Пример 4.5.
Чтобы преобразовать элементы списка с помощью такой функции, пишем сразу:
(defun duble (xl) (map-el #'tuple xl)) ; дублирование элементов (duble '(1(a)())) ; = ((1 . 1)((a)a)(()))
Немногим сложнее организовать покомпонентную обработку двух списков.
Построить ассоциативный список, т.е. список пар из имен и соответствующих им значений, по заданным спискам имен и их значений:
(defun pairl (al vl) ; Ассоциативный список (cond ; Пока AL не пуст, (al (cons (cons (car al) (car vl)) ; пары из <голов>. (pairl (cdr al) (cdr vl)) ; Если VL исчерпается, ; то CDR будет давать NIL ) ) ) )
(pair '(один два two three) '(1 2 два три)) ; = ((один . 1)(два . 2)(two . два)(three . три))
Пример 4.6.
Определить функцию покомпонентной обработки двух списков с помощью заданной функции fn:
(defun map-comp (fn al vl) ; fn покомпонентно применить ; к соотвественным элементам ; AL и VL (cond (xl (cons (funcall fn (car al) (car vl)) ; Вызов данного FN как функции (map-comp (cdr al) (cdr vl)) ) ) ) )
Пример 4.7.
Теперь покомпонентные действия над векторами, представленными с помощью списков, полностью в наших руках. Вот списки и сумм, и произведений, и пар, и результатов проверки на совпадение:
(map-comp #'+'(1 2 3) '(4 6 9)) ; = (5 8 12) Суммы (map-comp #'*'(1 2 3) '(4 6 9)) ; = (4 12 27) Произведения (map-comp #'cons'(1 2 3) '(4 6 9)) ; = ((1 . 4) (2 . 6) (3 . 9)) Пары (map-comp #'eq'(4 2 3) '(4 6 9)) ; = (T NIL NIL) Сравнения
Достаточно уяснить, что надо делать с элементами списка, остальное довершит функционал map-comp, отображающий этот список в список результатов заданной функции.
Для заданного списка вычислим ряд его атрибутов, а именно - длина, первый элемент, остальные элементы списка без первого.
(defun mapf (fl el) (cond ; Пока первый аргумент не пуст, (fl (cons (funcall (car fl) el) ; применяем очередную функцию ; ко второму аргументу (mapf (cdr fl) el) ; и переходим к остальным функциям, ) ) ) ) ; собирая их результаты в общий ; список
(mapf '(length car cdr) '(a b c d)) ; = (4 a (b c d))
Пример 4.8.
Композициями таких функционалов можно применять серии функций к списку общих аргументов или к параллельно заданной последовательности списков их аргументов. Естественно, и серии, и последовательности представляются списками.
Композиции функционалов, фильтры, редукции
Вызовы функционалов можно объединять в более сложные структуры таким же образом, как и вызовы обычных функций, а их композиции можно использовать в определениях новых функций. Композиции функционалов позволяют создавать и более мощные построения, достаточно ясные, но требующие некоторого внимания.
Декартово произведение хочется получить определением вида:
(defun decart (x y) (map-el #' (lambda (i) (map-el #' (lambda (j) (list i j)) y) ) x) )
Пример 4.10.
Но результат вызова
(decart '(a s d) '( e r t))
дает
(((A E) (A R) (A T)) ((S E) (S R) (S T)) ((D E) (D R) (D T)))
вместо ожидаемого
((A E) (A R) (A T) (S E) (S R) (S T) (D E) (D R) (D T))
Дело в том, что функционал map-el, как и map-comp (пример 4.7), собирает результаты отображающей функции в общий список с помощью операции cons так, что каждый результат функции образует отдельный элемент.
А по смыслу задачи требуется, чтобы список был одноуровневым.
Посмотрим, что получится, если вместо cons при сборе результатов воспользоваться функцией append.
Пусть дан список списков. Нужно их все сцепить в один общий список.
(defun list-ap (ll) (cond (ll (append (car ll) (list-ap (cdr ll)) ) ) ) )
(list-ap '((1 2)(3 (4)))) ; = (1 2 3 (4))
Пример 4.11.
Тогда по аналогии можно построить определение функционала map-ap:
(defun map-ap (fn ll) (cond (ll (append (funcall fn (car ll) ) (map-ap fn (cdr ll) ) ) ) ) )
(map-ap 'cdr '((1 2 3 4) (2 4 6 8) (3 6 9 12))) ; = (2 3 4 4 6 8 6 9 12)
Следовательно, интересующая нас форма результата может быть получена:
(defun decart(x y) (map-ap #'(lambda(i) (map-el #'(lambda(j)(list i j)) y))x)) (decart '(a s d) '(e r t)) ; = ((A E)(A R)(A T)(S E)(S R)(S T)(D E)(D R)(D T))
Сцепление результатов отображения с помощью append обладает еще одним полезным свойством: при таком сцеплении исчезают вхождения пустых списков в результат. А в Лиспе пустой список используется как ложное значение, следовательно, такая схема отображения пригодна для организации фильтров. Фильтр отличается от обычного отображения тем, что окончательно собирает не все результаты, а лишь удовлетворяющие заданному предикату.
Построить список голов непустых списков можно следующим образом:
(defun heads (xl) (map-ap #'(lambda (x) (cond (x (cons (car x) NIL)))) ; временно голова размещается в список, ; чтобы потом списки сцепить xl ) ) (heads '((1 2) () (3 4) () (5 6)) ) ; = (1 3 5)
Пример 4.12.
Рассмотрим еще один типичный вариант применения функционалов. Представим, что нас интересуют некие интегральные характеристики результатов, полученных при отображении, например, сумма полученных чисел, наименьшее или наибольшее из них и т.п. В таком случае говорят о свертке результата или его редукции. Редукция заключается в сведении множества элементов к одному элементу, в вычислении которого задействованы все элементы множества.
Подсчитать сумму элементов заданного списка.
(defun sum-el ( xl) (cond ((null xl) 0) (xl (+ (car xl) (sum-el (cdr xl) ) ) ) ) )
(sum-el '(1 2 3 4) ) ; = 10
Пример 4.13.
Перестроим такое определение, чтобы вместо <+> можно было использовать произвольную бинарную функцию:
(defun red-el (fn xl) (cond ((null xl) 0) (xl (funcall fn (car xl) (red-el fn (cdr xl) ) ) ) ) ) (red-el '+ '(1 2 3 4) ) ; = 10
В какой-то мере map-ap ведет себя как свертка - она сцепляет результаты без сохранения границ между ними.
Такие формулы удобны при моделировании множеств, графов и металингвистических формул, а к их обработке сводится широкий класс задач не только в информатике.
Отображения структур данных и функционалы
Отображения обычно используются при анализе и обработке данных, представляющих информацию разной природы. Вычисление, кодирование, трансляция, распознавание - каждый из таких процессов использует исходное множество цифр, шаблонов, текстов, идентификаторов, по которым конкретная отображающая функция находит пронумерованный объект, строит закодированный текст, выделяет идентифицированный фрагмент, получает зашифрованное сообщение. Таким образом работает любое введение обозначений - от знака происходит переход к его смыслу.
Отображения - ключевой механизм информатики. Построение любой информационной системы сопровождается определением и реализацией большого числа отображений. Сначала выбираются данные, с помощью которых представляется информация. В результате по данным можно восстановить представленную ими информацию - извлечь информацию из данных (по записи числа восстановить его величину). Потом конструируется набор структур, достаточный для размещения и обработки данных и программ в памяти компьютера (по коду команды можно выбрать хранимую в памяти подпрограмму, которая построит новые коды чисел или структур данных).
Говорят, что отображение существует, если задана пара множеств и отображающая функция, для которой первое множество - область определения, а второе - область значения. При определении отображений, прежде всего, должны быть ясны следующие вопросы:
что представляет собой отображающая функция;как организовано данное, представляющее отображаемое множество;каким способом выделяются элементы отображаемого множества, передаваемые в качестве аргументов отображающей функции.
Это позволяет задать порядок перебора множества и метод передачи аргументов для вычисления отображающей функции. При обходе структуры, представляющей множество, отображающая функция будет применена к каждому элементу множества.
Проще всего выработать структуру множества результатов, подобную исходной структуре. Но возможно не все полученные результаты нужны или требуется собрать их в иную структуру, поэтому целесообразно прояснить заранее еще ряд вопросов:
Подведение итогов
Показанные построения достаточно разнообразны, чтобы можно было сформулировать, в чем преимущества применения техники функционального программирования:
отображающие функционалы позволяют строить программы из крупных действий;
функционалы обеспечивают гибкость отображений;определение функции может совсем не зависеть от конкретных имен;с помощью функционалов можно управлять выбором формы результатов;
параметром функционала может быть любая функция, преобразующая элементы структуры;функционалы позволяют формировать серии функций от общих данных;
встроенные в Clisp функционалы приспособлены к покомпонентной обработке произвольного числа параметров;любую систему взаимосвязанных функций можно преобразовать к одной функции, используя вызовы безымянных функций.
пока список не пуст
|
(defun next (xl) ; Следующие числа*) (cond ; пока список не пуст (xl(cons(1+(car xl)) ; прибавляем 1 к его голове (next(cdr xl)) ; и переходим к остальным, ) ) ) ) ; собирая результаты в список (next'(1 2 5)) ; = (2 3 6) |
| Пример 4.1. |
| Закрыть окно |
|
(defun 1st (xl) ; "головы" элементов = CAR (cond ; пока список не пуст (xl (cons (caar xl); выбираем CAR от его головы (1st (cdr xl)) ; и переходим к остальным, ) ) ) ) ; собирая результаты в список (1st'((один два)(one two)(1 2)) ) ; = (один one 1) |
| Пример 4.2. |
| Закрыть окно |
|
(defun lens (xl) ; Длины элементов (cond ; Пока список не пуст (xl (cons (length (car xl)) ; вычисляем длину его головы (lens (cdr xl)); и переходим к остальным, ) ) ) ) ; собирая результаты в список (lens'((1 2)()(a b c d)(1(a b c d)3)) ) ; = (2 0 4 3) |
| Пример 4.3. |
| Закрыть окно |
| ( defun sqw (x)(* x x)) ; Возведение числа в квадрат (sqw 3) ; = 9 |
| Пример 4.4. |
| Закрыть окно |
| (defun tuple (x) (cons x x)) (tuple 3) (tuple 'a) (tuple '(Ха)) ; = (3 . 3) ; = (a . a) ; = ((Ха) . (Ха)) = ((Ха) Ха) ; - это одно и то же! |
| Пример 4.5. |
| Закрыть окно |
|
(defun pairl (al vl) ; Ассоциативный список (cond ; Пока AL не пуст, (al (cons (cons (car al) (car vl)) ; пары из <голов>. (pairl (cdr al) (cdr vl)) ; Если VL исчерпается, ; то CDR будет давать NIL ) ) ) ) (pair '(один два two three) '(1 2 два три)) ; = ((один . 1)(два . 2)(two . два)(three . три)) |
| Пример 4.6. |
| Закрыть окно |
| (defun map-comp (fn al vl) ; fn покомпонентно применить ; к соотвественным элементам ; AL и VL (cond (xl (cons (funcall fn (car al) (car vl)) ; Вызов данного FN как функции (map-comp (cdr al) (cdr vl)) ) ) ) ) |
| Пример 4.7. |
| Закрыть окно |
|
(defun mapf (fl el) (cond ; Пока первый аргумент не пуст, (fl (cons (funcall (car fl) el) ; применяем очередную функцию ; ко второму аргументу (mapf (cdr fl) el) ; и переходим к остальным функциям, ) ) ) ) ; собирая их результаты в общий ; список (mapf '(length car cdr) '(a b c d)) ; = (4 a (b c d)) |
| Пример 4.8. |
| Закрыть окно |
|
( defun sqware (xl) (map-el #' (lambda (x) (* x x)) xl)) (defun duble (xl) (map-el #' (lambda (x) (cons x x)) xl)) |
| Пример 4.9. |
| Закрыть окно |
| ( defun decart (x y) (map-el #' (lambda (i) (map-el #' (lambda (j) (list i j)) y) ) x) ) |
| Пример 4.10. |
| Закрыть окно |
|
(defun list-ap (ll) (cond (ll (append ( car ll) (list-ap (cdr ll)) ) ) ) ) (list-ap '((1 2)(3 (4)))) ; = (1 2 3 (4)) |
| Пример 4.11. |
| Закрыть окно |
| (defun heads (xl) (map-ap #'(lambda (x) (cond (x (cons (car x) NIL)))) ; временно голова размещается в список, ; чтобы потом списки сцепить xl ) ) (heads '((1 2) () (3 4) () (5 6)) ) ; = (1 3 5) |
| Пример 4.12. |
| Закрыть окно |
|
(defun sum-el ( xl) (cond (( null xl) 0) (xl (+ (car xl) (sum-el (cdr xl) ) ) ) ) ) (sum-el '(1 2 3 4) ) ; = 10 |
| Пример 4.13. |
| Закрыть окно |
| (mapcar #'+ '(1 2 3) '(4 5 6)) ; = (5 7 9) (mapcar #'list '(1 2 3)'(4 5 6)) ; = ((1 4)(2 5)(3 6)) (defun evlis (args) (mapcar #'eval args)) ; вычисление аргументов |
| Пример 4.14. |
| Закрыть окно |
| (maplist #'list '(1 2 3)'(4 5 6)) ; = (((1 2 3) (4 5 6)) ((2 3) (5 6)) ((3) (6))) |
| Пример 4.15. |
| Закрыть окно |
| (mapc #'list '(1 2 3)'(4 5 6)) ; = (1 2 3) (mapl #'list '(1 2 3)'(4 5 6)) ; = (1 2 3) |
| Пример 4.16. |
| Закрыть окно |
Встроенные функционалы (Clisp)
Отображающий функционал можно написать самим, а можно и воспользоваться одним из встроенных. Согласно стандарту, в реализацию языка Clisp обычно включены функционалы: map, mapcar,maplist, mapcan, mapcon, mapc, mapl [6, 7]. Каждый из них покомпонентно обработает любой набор списков. Отличаются они схемами выбора аргументов для отображающей функции, характером воздействия на исходные данные и оформлением результатов, передаваемых объемлющим формулам.
Map
( map result-type function sequences ... )
Функция function вызывается на всех первых элементах последовательностей, затем на всех вторых и т.д. Из полученных результатов function формируется результирующая последовательность, строение которой задается параметром result-type с допустимыми значениями cons, list, array, string, NIL.
Mapcar
( mapcar function list ... )
Функция function применяется к первым элементам списков, затем ко вторым и т.д. Другими словами, function применяется к <головам> методично сокращающихся списков, и результаты применения собираются в результирующий список.
(mapcar #'+ '(1 2 3) '(4 5 6)) ; = (5 7 9) (mapcar #'list '(1 2 3)'(4 5 6)) ; = ((1 4)(2 5)(3 6)) (defun evlis (args) (mapcar #'eval args)) ; вычисление аргументов
Пример 4.14.
(Без учета ассоциативного списка)
(defun evlis (args AL) (mapcar #'(lambda (x) (eval x AL)) args)) Maplist
( maplist function list ... )
Функционал аналогичен mapcar, но function применяется к <<хвостам>> списков list, начиная с полного списка.
(maplist #'list '(1 2 3)'(4 5 6)) ; = (((1 2 3) (4 5 6)) ((2 3) (5 6)) ((3) (6)))
Пример 4.15. Mapc и Mapl
Оба функционала работают как mapcar и maplist, соответственно, за исключением того, что они в качестве формального результата выдают первый список (своеобразная аналогия с формальными аргументами).
(mapc #'list '(1 2 3)'(4 5 6)) ; = (1 2 3) (mapl #'list '(1 2 3)'(4 5 6)) ; = (1 2 3)
Пример 4.16. Mapcan и Mapcon
И эти два функционала аналогичны mapcar и maplist, но формирование результатов происходит не с помощью операции cons, которая строит данные в новых блоках памяти, а с помощью деструктивной функции nconc, которая при построении новых данных использует память исходных данных, из-за чего исходные данные могут быть искажены.
В общем случае, отображающие функционалы представляют собой различные виды структурной итерации или итерации по структуре данных. При решении сложных задач полезно использовать отображения и их композиции, а также иметь в виду возможность создания своих функционалов.
Map-into отображает результат в конкретную последовательность.
Функции
Ситуация, когда атом обозначает функцию, реализационно подобна той, в которой атом обозначает аргумент. Если функция рекурсивна, то ей надо дать имя. Теоретически это делается с помощью формы LABEL, которая связывает название с определением функции в ассоциативном списке (а-списке). Название связано с определением функции точно так же, как переменная связана со своим значением. На практике LABEL используется редко. Удобнее связывать название с определением другим способом. Это делается путем размещения определения функции в списке свойств атома (р-список), символизирующего ее название. Выполняет данную операцию псевдо-функция DEFUN, описанная в начале этой лекции. Когда APPLY интерпретирует функцию, представленную атомом, она исследует р-список до поиска в а-списке. Таким образом, DEFUN будет опережать LABEL.
Тот факт, что большинство функций — константы, определенные программистом, а не переменные, изменяемые программой, вызван отнюдь не каким-либо недостатком функционального программирования. Напротив, он указывает на потенциал подхода, который мы не научились использовать лучшим образом. (Работы по теории компиляции, оптимизации и верификации программ, смешанным вычислениям, суперпрограммированию и т.п. активно используют средства функционального программирования.)
Системы функционального программирования обеспечивают возможность манипулирования функциональными переменными так же, как и обычными. Но организуется это с помощью ряда специальных функций, осуществляющих переход от символов, изображающих функции, к функциональным объектам, представленным этими символами. Такой переход может быть реализован в рамках любого языка программирования, но на Лиспе он выглядит естественно и поддерживается в любой Лисп-системе. Рассмотрим средства Clisp, обеспечивающие структурирование функциональных объектов.
Labels — позволяет из списка определений функций формировать контекст, в котором вычисляются выражения.
Flet — специальная функция, позволяющая вводить локальные нерекурсивные функции.
defun — позволяет вводить новые определения на текущем уровне.
(labels ( (INTERSECTION (x y)
(let* ( (N-X (null x)) (MEM-CAR (member (car x) y)) (INT #'intersection) ) ; конец списка локальных выраженийlet*
(flet ((f-tail (fn sx sy) (apply fn (list (cdr sx) sy)) ) (cons-f-tail (fn sx sy) (cons (car sx) (apply fn (list (cdr sx) sy)) )) ) ; конец списка нерекурсивных функций flet
(COND (N-X NIL) ; выражение, использующее (MEM-CAR (cons-f-tail INT x y) ) ; локальные определения функций (T (f-tail INT x y)) ) ; из контекстов flet и ; labels ) ; выход из контекста flet ) ; выход из контекста let* ) ; завершено определение INTERSECTION ) ; конец списка локальных рекурсивных функций
(defun UNION (x y) (let ( (a-x (CAR x)) (d-x (CDR x)) ) (COND ((NULL x) y) ((MEMBER a-x y) (UNION d-x y) ) (T (CONS a-x (UNION d-x y)) ) ) ) ) ; завершено определение на текущем уровне
(INTERSECTION '(A1 A2 A3) '(A1 A3 A5)) (UNION '(X Y Z) '(U V W X)) ) ; выход из контекста labels
Функции на машинном языке (низкоуровневые)
Некоторые функции вместо определений с помощью S-выражений закодированы как замкнутые машинные подпрограммы. Такая функция будет иметь особый индикатор в списке свойств с указателем, который позволяет интерпретатору связаться с подпрограммой. Существует три случая, в которых низкоуровневая подпрограмма может быть включена в систему:
Подпрограмма закодирована внутри Лисп-системы. Функция кодируется пользователем вручную на языке типа ассемблера. Функция сначала определяется с помощью S-выражения, затем транслируется компилятором. Компилированные функции могут выполняться в 2100 раз быстрее, чем интерпретироваться.
Интерпретирующая система. Реализационное уточнение интерпретации
Эта глава предназначена для реализационного уточнения уже известных теоретических рассуждений. Ряд уточнений показан на примере, представляющем программу, которая определяет три функции union, intersection и member, а затем применяет эти функции к нескольким тестам [1]. На этом примере будут рассмотрены средства и методы, обеспечивающие удобочитаемость функциональных программ и удобство их развития при отладке. Как правило, удобство достигается включением в систему дополнительных функций для решения проблем, принципиальное решение которых уже обеспечено на уровне теории.
Функции union и intersection применяют к множествам, каждое множество представлено в виде списка атомов. Заметим, что все функции рекурсивны, а union и intersection используют member. Схематично работу этих функций можно выразить следующим образом:
member = lambda [a;x] [ null[x] ==>> Nil ] [ eq[a;car[x]] ==>> T ] [ T ==>> member[a;cdr[x]] ]
union = lambda[x;y] [ null[x] ==>> y ] [ member[car[x];y] ==>> union[cdr[x];y] ] [ T ==>> cons[car[x];union[cdr[x];y]] ]
intersection = lambda [x;y] [ null[x] ==>> NIL ] [ member[car[x];y] ==>> cons[car[x];intersection[cdr[x];y]] ] [ T ==>> intersection[cdr[x];y] ]
Определяя эти функции на Лиспе, мы используем дополнительную псевдо-функцию DEFUN, объединяющую эффекты lambda и label. Программа выглядит так:
(DEFUN MEMBER (A X) (COND ((NULL X) Nil) ((EQ A (CAR X)) T) (T (MEMBER A (CDR X)) ) ) )
(DEFUN UNION (X Y) (COND ((NULL X) Y) ((MEMBER (CAR X) Y) (UNION (CDR X) Y) ) (T (CONS (CAR X) (UNION (CDR X) Y))) )) ) ) )
(DEFUN INTERSECTION (X Y) (COND ((NULL X) NIL) ((MEMBER (CAR X) Y) (CONS (CAR X) (INTERSECTION (CDR X) Y)) ) (T (INTERSECTION (CDR X) Y)) ) )
(INTERSECTION '(A1 A2 A3) '(A1 A3 A5)) (UNION '(X Y Z) '(U V W X))
Эта программа предлагает вычислить пять различных форм.
Первые три формы сводятся к применению псевдо-функции DEFUN.
Псевдо-функция — это функция, которая выполняется ради ее воздействия на систему, тогда как обычная функция — ради ее значения.
DEFUN заставляет функции стать определенными и допустимыми в системе равноправно со встроенными функциями. Ее значение — имя определяемой функции, в данном случае — member, union, intersection. Более точно можно сказать, что полная область значения псевдо-функции DEFUN включает в себя некоторые доступные ей части системы, обеспечивающие хранение информации о функциональных объектах, а формальное ее значение — атом, символизирующий определение функции.
Значение четвертой формы — (A1 A3). Значение пятой формы — (Y Z C B D X). Анализ пути, по которому выполняется рекурсия, показывает, почему элементы множества появляются именно в таком порядке.
В этом примере продемонстрировано несколько элементарных правил написания функциональных
программ, сложившихся при реализации интерпретатора Лисп 1.5 в дополнение к идеализированным правилам, сформулированным в строгой теории Лиспа. (С точностью до разницы между EVALQUOTE — EVAL.)
Программа состоит из последовательности вычисляемых форм. Если форма список, то ее первый элемент интерпретируется как функция. Остальные элементы списка — аргументы для этой функции. Они вычисляются с помощью EVAL, а функция применяется к ним с помощью APPLY, и полученное значение выводится как результат программы. Особого формата для записи программ не существует. Границы строк игнорируются. Формат программы, включая идентификацию, выбран просто для удобства чтения. Любое число пробелов и концов строк можно разместить в любой точке программы, но не внутри атома.Не используются (QUOTE T), (QUOTE NIL). Вместо них применяется T, NIL, что влечет за собой соответствующее изменение определения EVAL. Атомы должны начинаться с букв, чтобы их можно было легко отличать от чисел. Может использоваться точечная нотация. Любое число пробелов перед или после точки, свыше одного, будет игнорироваться (один пробел нужен обязательно при соседстве с атомом). Точечные пары могут появляться как элементы списка, и списки могут быть элементами точечных пар.
((A . B) X (C . (E F D))) — есть допустимое S-выражение. Оно может быть записано как
((A . B) . ( X . ((C . (E . ( F . (D . Nil)))) . Nil)))
или
((A . B) X (C E F D)) Форма типа (A B C . D) есть сокращение для (A . ( B . ( C . D) )). Любая другая расстановка точек на одном уровне есть ошибка, например (A. B C). Набор основных функций предоставляется системой. Другие функции могут быть введены программистом. Порядок введения функций не имеет значения. Любая функция может использоваться в определении другой функции.
Вывод S-выражений на печать и в файлы выполняет псевдо-функция print, чтение данных обеспечивает псевдо-функция read. Программа из файла может быть загружена
псевдо-функцией load.
(PRINT (INTERSECTION '(A1 A2 A3) '(Al A3 A5)) ) (PRINT (UNION '(X Y Z) '(U V W X)) ) (PRINT (UNION (READ) '(1 2 3 4)) ) ; объединение вводимого списка со списком ; '(1 2 3 4)
Константы
Иногда говорят, что константы представляют сами себя, в противоположность
переменным, представляющим что-то другое. Это не вполне точно, поскольку обычно константы представляют как a, b, c, ..., а переменные как x, y, z, ... — но и то, и другое выглядит как атом. Удобнее говорить, что одна переменная ближе к константам, чем другая, если она связана на более высоком уровне и ее значение изменяется не столь часто.
Обычно переменная считается связанной в области действия лямбда-конструктора функции, который связывает переменную внутри тела определения функции путем размещения пары из имени и значения в начале а-списка. В том случае, когда
переменная всегда имеет определенное значение независимо от текущего состояния а-списка, она будет называться константой. Такую неизменяемую связь можно установить, помещая пару (a . v) в конец a-списка. Но в реальных системах это организовано с помощью так называемого списка свойств атома, являющегося представлением переменной. Каждый атом имеет свой p-список (property list), доступный через хэш-таблицу идентификаторов, что действует эффективнее, чем a-список. С каждым атомом связана специальная структура данных, в которой размещается имя атома, его значение, определение функции, представляемой этим же атомом, и список произвольных свойств, помеченных индикаторами. При вычислении переменных EVAL исследует эту структуру до выполнения поиска в а-списке. Такое устройство переменных не позволяет им служить переменных в а-списке.
Константы могут быть заданы программистом. Чтобы переменная X стала обозначением для (A B C D), надо воспользоваться псевдо-функцией defconstant.
(DefConstant X '(A B C D))
Особый интерес представляет тип констант, которые всегда обозначают себя, Nil — пример такой константы. Такие константы как T, Nil и другие самоопределимые константы (числа, строки) не могут использоваться в качестве переменных. Cмысл чисел и строк не может быть изменен с помощью defconstant.
Неподвижная точка и самоприменимость функций
Возможность использования безымянных определений функций не вполне очевидна для вспомогательных рекурсивных функций, так как их имена нужны в их собственных определениях. Но при необходимости и определение рекурсивной функции можно привести к форме, не зависящей от ее имени. Такие имена формально работают как связанные переменные, т.е. их смысл не зависит от имени — нечто вроде местоимения. Это позволяет выполнять систематическую замену названия функции на другие символы или выражения.
Пример (предложен В.А.Потапенко).
Преобразуем определение факториала в самоприменимую безымянную форму.
Для этого нужно:
преобразовать исходное определение в самоприменимую форму; избавиться от собственного имени функции.
Традиционное определение факториала:
(defun N! (n) (cond ((eq n 0) 1) (T (* n (N! (- n 1)))) ; Факториал
; Выход из рекурсии
; Рекурсивный виток с редукцией аргумента ) ) ; и умножением на результат предыдущего витка
Строим самоприменимое определение факториала:
(defun N!_self (f n) ; Обобщенная функция, ; равносильная факториалу при f = N!_self (cond ((eq n 0)1) (T (* n (apply f (list f (- n 1))))) ; применение функции f ; к списку из уменьшенного аргумента ) )
Использовать это определение можно следующим образом:
(N!_self #'N!_self 3) ; = 6 =
или
(apply 'N!_self '(N!_self 4)) ; = 24 =
При таких аргументах оно эквивалентно исходному определению факториала. Теперь избавимся от названия функции:
((lambda (f n ) ; безымянная функция, равносильная факториалу ; при f = N!_self
(cond ((eq n 0)1) (t (* n ( f (list f (- n 1))))) ))
Использовать это определение можно в следующей форме:
((lambda (f n ) (cond ((eq n 0)1) (t (* n (apply f (list f (- n 1))))) )) ; функция
(lambda (f n ) (cond ((eq n 0)1) (t (* n (apply f (list f (- n 1))))) )) ;первый аргумент — f 5 ; второй аргумент — n ) ; = 120
или
(apply
#'(lambda (f n ) (cond ((eq n 0)1)(t (* n (apply f (list f (- n 1))))) ) ) ; функция '((lambda (f n ) (cond ((eq n 0)1) (t (* n (apply f (list f (- n 1))))) )) 6 ) ; список аргументов )) ; = 720
Можно записать этот текст программы (код) без дублирования определения функции:
(lambda (n) ( (lambda (f) (apply f f n)) #'(lambda (f n ) (cond ((eq n 0)1) (t (* n (apply f (list f (- n 1)))) ) ) ; внутренняя функция f ) ))
И использовать полученное определение следующим образом:
((lambda (n) ((lambda (f) (apply f (list f n))) #'(lambda (f n ) (cond ((eq n 0)1) (t (* n (apply f (list f (- n 1))))) ) ) )) 6 ) ; = 120 )
Сокращаем совпадающие подфункции и получаем форму, в которой основные содержательные компоненты локализованы:
((lambda (n) (flet ((afl (f n) (apply f (list f n)) ))
((lambda (f) (afl f n)) #'(lambda (f n ) (cond ((eq n 0)1) (t (* n (afl f (- n 1)))) ))))) 6 ) ; = 720 )
Таким образом, определение рекурсивной функции можно преобразовать к безымянной форме. Техника эквивалентных преобразований позволяет поддерживать целостность системы функций втягиванием безымянных вспомогательных функций внутрь тела основного определения. Верно и обратное: любую конструкцию из лямбда-выражений можно преобразовать в систему отдельных функций.
Такое, пусть не самое понятное, определение позволяет получить больше, чем просто скорость исполнения кода и его переносимость. Техника функциональных определений и их преобразований позволяет рассматривать решение задачи с той точки зрения, с какой это удобно при постановке задачи, с естественной степенью подробности, гибкости и мобильности.
специальная функция function (#') обеспечивает доступ к функциональному объекту, связанному с атомом, а функция funcall обеспечивает применение функции к произвольному числу ее аргументов.
(funcall f a1 a2 ... ) = (apply f (list a1 a2 ...))
Разрастание числа функций, манипулирующих функциями в Clisp, связано с реализационным различием структурного представления данных и представляемых ими функций.
Переменные
Переменная — это символ, который используется для представления аргумента функции.
Таким образом, возвращаясь к Дж.Мак-Карти [1]:
"Можно написать "a + b, где a = 341 и b = 216". В такой ситуации не может быть недоразумений, и все согласятся, что ответ есть 557. Чтобы получить этот результат, необходимо заменить переменные фактическими значениями, и затем сложить два числа (на арифмометре, например).
Одна из причин, по которой в этом случае не возникает недоразумений, состоит в том, что "a" и "b" не есть приемлемые входы для арифмометра, и следовательно, очевидно, что они только представляют фактические аргументы. При символьных вычислениях ситуация может быть более сложной. Атом может быть как переменной, так и фактическим аргументом. К дальнейшему усложнению приводит то обстоятельство, что некоторые из аргументов могут быть переменными, вычисляемыми внутри вызова другой функции. В таких случаях интуитивный подход может подвести. Для эффективного программирования в функциональном стиле необходимо более точное понимание формализмов.
Чтобы не обескураживать читателей, следует заметить, что здесь ничего принципиально нового нет. Все, что сейчас рассматривается, может быть логически выведено из правил представления
программ в виде S-выражений или из определения универсальных функций eval/apply, и является их непосредственным следствием, возможно, не вполне очевидным.
Любой формализм для переменных сводится к лямбда-обозначению. Часть интерпретатора, которая при вычислении функций связывает переменные, называется APPLY. Когда APPLY встречает функцию, начинающуюся с LAMBDA, список переменных попарно связывается со списком аргументов и добавляется к началу а-списка. При вычислении функции могут быть обнаружены переменные. Они вычисляются поиском в а-списке. Если переменная встречается несколько раз, то используется последнее или самое новое значение. Часть интерпретатора, которая делает это, называется EVAL. Проиллюстрируем данное рассуждение на примере.
Предположим, что интерпретатор получает следующее S-выражение: ((LAMBDA (X Y) (CONS X Y)) 'A 'B)
Функция:((LAMBDA (X Y) (CONS X Y)) 'A 'B)
Аргументы: (A B)
EVAL0 через EVAL передает эти аргументы функции APPLY. (См. лек. 3). (apply #’(LAMBDA (X Y) (CONS X Y)) ‘(A B) Nil )
APPLY свяжет переменные и передаст функцию и удлиннившийся а-список EVAL для вычисления. (eval ‘(CONS X Y) ‘ ((X . A) (Y . B) Nil))
EVAL вычисляет переменные и сразу передает их консолидации, строящей из них бинарный узел. (Cons ‘A ’B) = (A . B)
EVAL вычисляет переменные и сразу передает их консолидации, строящей из них бинарный узел.
Реальный интерпретатор пропускает один шаг, требуемый формальным определением универсальных функций".
На практике сложилась традиция включать в систему функционального программирования
специальные функции, обеспечивающие иерархию контекстов, в которых переменные обладают определенным значением. Для Clisp это let и let*.
Let сопоставляет локальным переменным независимые выражения. С ее помощью можно вынести из сложного определения любые совпадающие подвыражения.
(defun UNION (x y)
(let ( (a-x (CAR x)) (d-x (CDR x)) ) ; конец списка локальных именованных значений
(COND ((NULL x) y) ((MEMBER a-x y) (UNION d-x y) ) ; использование локальных (T (CONS a-x (UNION d-x y)) ) ; значений из контекста ) ) ; завершение контекста let )
Let* — сопоставляет локальным переменным взаимосвязанные выражения. Она позволяет дозировать сложность именуемых подвыражений.
(defun member (a x) (let* ( (n-x (null x)) (a-x (car x)) (d-x (cdr x)) (e-car (eq a a-x)) ) ; список локально именованных выражений
(COND (N-X Nil) ; использование (E-CAR T) ; именованных (T (MEMBER A D-X)) ; выражений ) ) ; выход из контекста именованных выражений )
(Эквивалентность с точностью до побочного эффекта.)
Глобальные переменные можно объявить с помощью специальной функции defparameter.
(DefParameter glob '(a b c))
Значение такой переменной доступно в любом контексте, оно может быть переопределено. Возможно оттеснение одноименными локальными переменными с восстановлением при выходе из соответствующих контекстов. При выполнении кода программ:
(let ((glob 12))(print glob)) (print glob)
напечатано будет:
12 (A B C)
Пример (CAR '(A B))
| (CAR '(A B)) = (CAR (QUOTE(A B)) |
| Пример 5.2. |
| Закрыть окно |
| (CONS 'A '(B . C)) |
| Пример 5.3. |
| Закрыть окно |
| ((CAR (QUOTE (A . B))) CDR (QUOTE (C . D))) |
| Пример 5.4. |
| Закрыть окно |
Программы для Лисп-интерпретатора.
Цель этой части — помочь избежать некоторых общих ошибок при отладке программ.
(CAR '(A B)) = (CAR (QUOTE(A B))
Пример 5.2.
Функция: CAR
Аргументы: ((A B))
Значение есть A. Заметим, что интерпретатор ожидает список аргументов. Единственным аргументом для CAR является (A B). Добавочная пара скобок возникает, т.к. APPLY подается список аргументов.
Можно написать (LAMBDA(X)(CAR X)) вместо просто CAR. Это корректно, но не является необходимым.
(CONS 'A '(B . C))
Пример 5.3.
Функция: CONS
Аргументы: (A (B . C))
Результат (A . (B . C)) программа печати выведет как (A B . C)
((CAR (QUOTE (A . B))) CDR (QUOTE (C . D)))
Пример 5.4.
Функция: CONS
Аргументы: ((CAR (QUOTE (A . B))) (CDR (QUOTE (C . D))))
Значением такого вычисления будет
((CAR (QUOTE (A . B))) . (CDR (QUOTE (C . D))))
Скорее всего, это совсем не то, чего ожидал новичок. Он рассчитывал вместо (CAR (QUOTE (A . B)) получить A и увидеть (A . D) в качестве итогового значения CONS. Интерпретатор настроен не на список уже готовых значений аргументов, а на список выражений, которые будут вычисляться до вызова функции. Кроме очевидного стирания апострофов
(CONS (CAR (QUOTE (A . B))) (CDR (QUOTE (C . D))) )
ниже приведены еще три правильных способа записи нужной формы. Первый состоит в том, что CAR и CDR части функции задаются с помощью LAMBDA в определении функции. Второй заключается в переносе CONS в аргументы и вычислении их с помощью EVAL при пустом а-списке. Третий — в принудительном выполнении константных действий в представлении аргументов.
((LAMBDA (X Y) (CONS (CAR X) (CDR Y))) '(A . B) '(C . D))
Функция: (LAMBDA (X Y) (CONS (CAR X) (CDR Y)))
Аргументы: ((A . B)(C . D))
(EVAL '(CONS (CAR (QUOTE (A . B))) (CDR (QUOTE (C . D)))) Nil)
Функция: EVAL
Аргументы: ((CONS (CAR (QUOTE (A . B))) (CDR (QUOTE (C . D)))) Nil)
Значением того и другого является (A . D)
((LAMBDA (X Y) (CONS (EVAL X) (EVAL Y))) '(CAR (QUOTE (A . B)))' (CDR (QUOTE (C . D))) )
Функция: (LAMBDA (X Y) (CONS (EVAL X) (EVAL Y)))
Аргументы: ((CAR (QUOTE (A . B))) (CDR (QUOTE (C . D))))
Решения этого примера показывают, что грань между функциями и данными достаточно условна — одни и те же вычисления можно осуществить при разном распределении промежуточных вычислений внутри выражения, передвигая эту грань.

Специальные формы
Обычно EVAL вычисляет аргументы функций до применения к ним функций с помощью APPLY. Таким образом, если EVAL задано (CONS X Y), то сначала вычисляются X и Y, а потом над полученными значениями работает CONS. Но если EVAL задано (QUOTE X), то X не будет вычисляться. QUOTE — специальная форма, которая препятствует вычислению своих аргументов.
Специальная форма отличается от других функций двумя свойствами. Ее аргументы не вычисляются, пока она сама не просмотрит свои аргументы. COND, например, имеет свой особый способ вычисления аргументов с использованием EVCON. Второе отличие заключается в том, что специальные формы могут иметь неограниченное число аргументов.
Деструктивные (разрушающие) преобразования структуры списков
Теория рекурсивных функций, изложенная в лекции 2, будет упоминаться далее как строгий, чистый или элементарный Лисп. Хотя этот язык универсален в смысле теории вычислимых функций от символьных выражений, он непрактичен как система программирования без дополнительного инструмента, увеличивающего выразительную силу и эффективность языка.
В частности, элементарный Лисп не имеет возможности модифицировать структуру списка. Единственная базисная функция, влияющая на структуру списка — это cons, а она не изменяет существующие списки, только создает новые. Функции, описанные в чистом Лиспе, такие как subst, в действительности не модифицируют свои аргументы, но делают модификации, копируя оригинал.
Элементарный Лисп работает как расширяемая система, в которой информация как бы никогда не пропадает. Set внутри Prog лишь формально смягчает это свойство, сохраняя ассоциативный список и моделируя присваивания теми же CONS.
Теперь же Лисп обобщается с точки зрения структуры списка добавлением структуроразрушающих средств — деструктивных базисных операций над списками rplaca и rplacd. Эти операции могут применяться для замены адреса или декремента любого слова в списке. Они используются ради их действия так же, как и ради их значения и называются псевдо-функциями.
(rplaca x y) заменяет адрес из x на y, эквивалент (car x) := y. Ее значение — x, но x, несколько отличающийся от того, что было раньше. На языке значений rplaca можно описать равенством
(rplaca x y) = (cons y (cdr x))
Но действие различное: никакие cons не вызываются и новые слова не создаются.
(rplacd x y) заменяет декремент x на y, эквивалент (cdr x) := y.
Эти операции должны применяться с осторожностью! Они могут в корне преобразить существующие определения и основную память. Их применение может породить циклические списки, приводящие к бесконечной печати или выглядящие бесконечными для таких функций как equal и subst.
Деструктивные функции используются при реализации списков свойств атома и ряда эффективных, но небезопасных, функций
Clisp-а, таких как nconc, mapc и т.п.
Для примера рассмотрим функцию mltgrp. Это преобразующая список функция, которая преобразует копию своего аргумента. Подфункция grp реорганизует подструктуру

Рис. 1.13. подструктура
в структуру из тех же атомов:
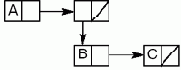
Рис. 1.14. структура из тех же атомов
Исходная функция делает это, создавая новую структуру и используя четыре cons. Из-за того, что в оригинале только три слова, по крайней мере, один cons необходим, а grp можно переписать с помощью rplaca и rplacd. Изменение состоит в следующем:

Рис. 1.15. новая структура
Пусть новое машинное слово строит (cons (cadr x) (cddr x)). Тогда указатель на него встраивается в x при вычислении формы:
(rplaca (cdr x) (cons (cadr x) (cddr x)))
Другое изменение состоит из удаления указателя на третье слово из второго слова.
Это выполняется как вычисление формы (rplaca (cdr x) NIL).
Функция pgrp теперь определяется как соотношение:
(pgrp x) = (rplacd (rplaca (cdr x) (cons (cadr x) (cddr )x))) NIL)
Функция pgrp используется, в сущности, ради ее действия. Ее значением, неиспользуемым, является подструктура ((B C)). Поэтому для mltgrp необходимо, чтобы pgrp выполнялось, а ее значение игнорировалось. Поскольку верхний уровень не должен копироваться, mltgrp не обязательно должна основываться на cons.
(pmltgrp L) =(COND ((null L) NIL) (T (pgrp (cdr L)) (pmltgrp (cdr L)) )))
prog2 — функция, вычисляющая свои аргументы. Ее значение — второй аргумент.
Значение pmltgrp — NIL. pgrp и pmltgrp — псевдо-функции.
Гибкий интерпретатор
В качестве примера повышения гибкости определений приведено упрощенное определение Лисп-интерпретатора на Лиспе, полученное из М-выражения, приведенного Дж. Мак-Карти в описании Lisp 1.5
[1 (не найдено)].
Ради удобочитаемости здесь уменьшена диагностичность, нет предвычислений и формы Prog. Лисп хорошо приспособлен к оптимизации программ. Любые совпадающие подвыражения можно локализовать и вынести за скобки, как можно заметить по передаче значения
"(ASSOC e al )".
Определения функций хранятся в ассоциативном списке, как и значения переменных.
Функция SUBR — вызывает примитивы, реализованные другими, обычно низкоуровневыми, средствами. ERROR — выдает сообщения об ошибках и сведения о контексте вычислений, способствующие поиску источника ошибки. Уточнена работа с функциональными аргументами:
(DEFUN EVAL (e al ) (COND
((EQ e NIL ) NIL ) ((ATOM e )((LAMBDA (v ) (COND (v (CDR v ) ) (T (ERROR 'undefvalue )) ) ) (ASSOC e al ) ) ) ((EQ (CAR e) 'QUOTE ) (CAR (CDR e )) ) ((EQ (CAR e) 'FUNCTION ) (LIST 'FUNARG (CADR fn ) al ) ) ((EQ (CAR e) 'COND ) (EVCON (CDR e ) al ) ) (T (apply (CAR e)(evlis (CDR e) al ) al ) ) ) )
(DEFUN APPLY (fn args al ) (COND ((EQ e NIL ) NIL ) ((ATOM fn ) (COND ((MEMBER fn '(CAR CDR CONS ATOM EQ )) (SUBR fn agrs al )) (T (APPLY (EVAL fn al ) args al )) ) )
((EQ (CAR fn ) 'LABEL ) (APPLY (CADDR fn ) args (CONS (CONS (CADR fn )(CADDR fn )) al ) ) )
((EQ (CAR fn ) 'FUNARG ) (APPLY (CDR fn ) args (CADDR fn)) )
((EQ (CAR fn ) 'LAMBDA ) (EVAL (CADDR fn ) (APPEND (PAIR (CADR fn ) args ) al )) (T (APPLY (EVAL fn al ) args al )) ) )
Определения assoc, append, pair, list — стандартны.
Примерно то же самое обеспечивают eval-p и apply-p, рассчитанные на использование списков свойств атома для хранения постоянных значений и функциональных определений. Индикатор category указывает в списке свойств атома на правило интерпретации функций, относящихся к отдельной категории, macro — на частный метод построения представления функции. Функция value реализует методы поиска текущего значения переменной в зависимости от контекста и свойств атомов.
(defun eval-p (e c) (cond ((atom e) (value e c)) ((atom (car e))(cond ((get (car e) 'category) ((get (car e) 'category) (cdr e) c) ) (T (apply-p (car e)(evlis (cdr e) c) c)) ) ) (T (apply-p (car e)(evlis (cdr e) c) c)) ))
(defun apply-p (f args c) (cond ((atom f)(apply-p (function f c) args c)) ((atom (car f))(cond ((get (car f) 'macro) (apply-p ((get (car f) 'macro) (cdr f) c) args c)) (T (apply-p (eval f e) args c)) ) ) (T (apply-p (eval f e) args c)) ))
Или то же самое с вынесением общих подвыражений во вспомогательные параметры:
(defun eval-p (e c) (cond ((atom e) (value e c)) ((atom (car e)) ((lambda (v) (cond (v (v(cdr e) c) ) (T (apply-p (car e)(evlis (cdr e) c) c)) )) (get (car e) 'category) ) ) (T (apply-p (car e)(evlis (cdr e) c) c)) ))
(defun apply-p (f args c) (cond ((atom f)(apply-p (function f c) args c)) ((atom (car f)) ((lambda (v) (cond (v (apply-p (v (cdr f) c) args c)) (T (apply-p (eval f e) args c)) ))(get (car f) 'macro) )) (T (apply-p (eval f e) args c)) ))
Расширение системы программирования при таком определении интерпретации осуществляется простым введением/удалением соответствующих свойств атомов и функций.
Полученная схема интерпретации допускает разнообразные категории функций и макросредства конструирования функций, позволяет задавать различные механизмы передачи параметров функциям. Так, в языке Clisp различают, кроме обычных, обязательных и позиционных, — необязательные (факультативные), ключевые и серийные(многократные, с переменным числом значений) параметры . Виды параметров обозначаются пометкой &optional, &key и &rest соответственно, размещаемой перед параметрами в
lambda списке формальных аргументов. При этом серийный параметр должен быть последним в списке.
(defun funcall (fn rest agrs) (apply fn args))
Необязательный параметр может иметь начальное значение, устанавливаемое по умолчанию, т.е. если этот параметр не задан при вызове функции. При отсутствии начального значения его роль играет Nil.
(defun ex-opt (space optional dot (line 'x)) (list space 'of dot 'and- line)) (ex-opt 'picture) (ex-opt 'picture 'circle) (ex-opt 'picture 'circle 'bars)
Пример 6.2.
Ключевые параметры, являясь необязательными, не зависят еще и от порядка вхождения в список аргументов. Незаданные аргументы по умолчанию связываются с Nil.
(defun keylist (a key x y z) (list a x y z)) (keylist 1 :y 2) ;= (1 NIL 2 NIL)
(defun LENGTH (L optional (V 0)) (cond ((null L) V) (T (+ 1 (LENGTH (cdr L)))) ) )
((LENGTH '(1 2) 3) ; = 5
(defun REVERSE (L optional (m Nil)) (cond ((null L) m) (T (REVERSE (cdr L) (cons (car L) m) )) ) )
(REVERSE '(1 2 3)) ; = (3 2 1) (REVERSE '(1 2 3) '(5 6)) ;= (3 2 1 5 6)
Пример 6.3.
Такой подход к работе параметрами часто освобождает от необходимости во вспомогательных функциях, что упрощает и определение Eval от обязательности упоминания а-списка. Если воспользоваться сводимостью (COND) к Nil при отсутствии истиного предиката и кое-где использовать отображения, то определение становится совсем компактным.

Представление структуры списка
В машине списки хранятся не как последовательности символов, а как структурные формы, построенные из машинных слов как частей деревьев, подобно записям в Паскале при реализации односвязных списков. При изображении структуры списка машинное слово рисуется как прямоугольник, разделенный на две части: адрес и декремент

Рис. 1.1. структура списка
Каждая из частей занимает фиксированное число разрядов, представляющее тэг и адрес. Если декремент слова "x" указывает на слово "y", то это можно выразить стрелками на схеме:

Рис. 1.2. схема
Теперь можно дать правило представления S-выражений в машине. Представление атомов будет пояснено ниже. В тех случаях, когда машинное слово в адресе или декременте содержит указатель на атом, данный атом отобразится как запись в соответствующем прямоугольнике:

Рис. 1.3. отображение атома в прямоугольнике
Правило представления неатомных S-выражений — начало со слова, содержащего указатель на car выражения в адресе иуказатель на cdr в декременте. Ниже нарисовано несколько схем S-выражений. По соглашению NIL обозначается как перечеркнутый по диагонали прямоугольник.

Рис. 1.4. обозначение NIL
вместо (A . B).

Рис. 1.5. (A . B)
Непосредственная польза от сопоставления графического вида с представлением списков в памяти поясняется при рассмотрении функций, работающих со списками, на следующем примере из [1]:
((M . N) X (M . N))
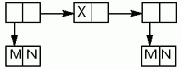
Рис. 1.8. пример
Возможное для списков использование общих фрагментов ((M . N) X (M . N)) может быть представлено графически:
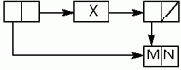
Рис. 1.9. графическое представление
В точности такую структуру непосредственно текстом представить невозможно, но ее можно построить с помощью одного из выражений выражений:
(let ((a '(M . N))) (setq b (list a 'X a)) ) ((lambda (a) (list a 'X a) )'(M . N))
Циклические списки обычно не поддерживаются. Такие списки не могут быть введены псевдо-функцией read, однако они могут возникнуть как результат вычисления некоторых функций, точнее, применения структуроразрушающих или деструктивных функций.
Печатное изображение таких списков имеет неограниченную длину. Например, структура

Рис. 1.10. структура
может распечатываться как ( A B C A B C ... ).
Преимущества структур списков для хранения S-выражений в памяти:
Размер и даже число выражений, с которыми программа будет иметь дело, можно не предсказывать. Кроме того, можно не организовать для размещения выражений блоки памяти фиксированной длины. Ячейки можно переносить в список свободной памяти, как только исчезнет необходимость в них. Даже возврат одной ячейки в список имеет значение, но если выражения хранятся линейно, то организовать использование лишнего или освободившегося пространства из блоков ячеек трудно.Выражения, являющиеся продолжением нескольких выражений, могут быть предоставлены только однажды.
Ниже следует простой пример, иллюстрирующий точность построения структур списка. Показаны два типа структур списка и описаны на Лиспе функции для преобразования одного типа в другой.
Предполагается, что дан список вида
L1 = ((A B C)(D E F ) ... (X Y Z))
представленный как

Рис. 1.11. точность построения структр списка
и нужно построить список вида
L2 = ((A (B C))(D (E F)) ... (X (Y Z)))
представленный как

Рис. 1.12. список вида
Рассмотрим типичную подструктуру (A (B C)) второго списка.
Она может быть построена из A,B и C с помощью
(cons ‘A (cons (cons ‘B (cons ‘C NIL)) NIL))
или, используя функцию list, можно то же самое записать как
(list ‘A (list ‘B ‘C))
В любом случае дан список x из трех атомов x = (A B C), аргументы A, B и C, используемые в предыдущем построении, можно найти как
A = (car x) B = (cadr x) C = (caddr x)
Первый шаг в получении L2 из L1 — это определение функции grp, строящей (X (Y Z)) из списка вида (X Y Z).
(grp x) = (list (car x) (list (cadr x) (caddr x)))
Здесь grp применяется к списку L1 в предположении, что L1 заданного вида.
Для достижения цели новая функция mltgrp определяется как
(mltgrp L) = (COND ((null L) NIL) (T (cons (grp (car L)) (mltgrp (cdr L)) )))
Итак, mltgrp, применяемая к списку L1, перебирает (X Y Z) по очереди и применяет к ним grp, чтобы установить их новую форму (X (Y Z)) до тех пор, пока не завершится список L1 и не построится новый список L2.
print x)
| (setq x 'y) (set x 'NEW) ( print x) (print y) |
| Пример 6.1. |
| Закрыть окно |
| (defun ex-opt ( space optional dot (line 'x)) (list space 'of dot 'and- line)) (ex-opt 'picture) (ex-opt 'picture 'circle) (ex-opt 'picture 'circle 'bars) |
| Пример 6.2. |
| Закрыть окно |
|
(defun LENGTH (L optional (V 0)) (cond (( null L) V) (T (+ 1 (LENGTH (cdr L)))) ) ) ((LENGTH '(1 2) 3) ; = 5 (defun REVERSE (L optional (m Nil)) (cond ((null L) m) (T (REVERSE (cdr L) (cons (car L) m) )) ) ) (REVERSE '(1 2 3)) ; = (3 2 1) (REVERSE '(1 2 3) '(5 6)) ;= (3 2 1 5 6) |
| Пример 6.3. |
| Закрыть окно |
Prog-выражения и циклы
Противопоставление функционального и императивного стилей программирования порой напоминает войну остроконечников с тупоконечниками. Существует большое число чисто теоретических работ, исследовавших соотношения между потенциалом того и другого подхода и пришедших к заключению о формальной сводимости в обе стороны при некоторых непринципиальных ограничениях на технику программирования. Методика сведения императивных программ в функциональные заключается в определении правил разметки или переписывания схемы программы в функциональные формы. Переход от функциональных программ к императивным технически сложнее: используется интерпретация формул над некоторой специально устроенной абстрактной машиной [3,
4]. На практике переложение функциональных программ в императивные выполнить проще, чем наоборот — может не хватать близких понятий.
С практической точки зрения любые конструкции стандартных языков программирования могут быть введены как функции, дополняющие исходную систему программирования, что делает их вполне легальными средствами в рамках функционального подхода. Надо лишь четко уяснить цену такого дополнения и его преимущества, обычно связанные с наследованием решений и привлечением пользователей. В первых реализациях Лиспа были сразу предложены специальные формы и структуры данных, служащие мостом между разными стилями программирования, а заодно смягчающие недостатки исходной, слишком идеализированной, схемы интерпретации S-выражений, выстроенной для учебных и исследовательских целей. Важнейшее такого рода средство, выдержавшее испытание временем — prog-форма, списки свойств атома и деструктивные операции, расширяющие язык программирования так, что становятся возможными оптимизирующие преобразования структур данных, программ и процессов, а главное — раскрутка систем программирования [1 (не найдено)].
Применение prog-выражений позволяет писать "паскалеподобные" программы, состоящие из операторов, предназначенных для исполнения. (Точнее "алголоподобные", т.к.
появились лет за десять до паскаля. Но теперь более известен паскаль.)
Для примера prog-выражения приводится императивное определение функции (Length *), сканирующей список и вычисляющей число элементов на верхнем уровне списка. Значение функции Length — целое число. Программу можно примерно описать следующими словами (Стилизация примера от МакКарти [1 (не найдено)].):
"Это функция одного аргумента L. Она реализуется программой с двумя рабочими переменными u и v. Записать число 0 в v. Записать аргумент L в u. A: Если u содержит NIL, то программа выполнена и значением является то, что сейчас записано в v. Записать в u cdr от того, что сейчас в u. Записать в v на единицу больше того, что сейчас записано в v. Перейти к A"
Эту программу можно записать в виде Паскаль-программы с несколькими подходящими типами данных и функциями. Строкам описанной выше программы в предположении, что существует библиотека Лисп-функций над списками на Паскале, соответствуют строки определения функции:
function LENGTH (L: list) : integer; label A; var U: list; V: integer; begin V := 0; U := l; A: if null (U) then LENGTH := V; U := cdr (U); V := V+1; goto A; end;
Переписывая в виде S-выражения, получаем программу:
(defun LENGTH (L) (prog (U V) (setq V 0) (setq U L) A (cond ((null U)(return V))) (setq U (cdr U)) (setq V (+ 1 V)) (go A) ) )
(LENGTH '(A B C D)) (LENGTH ‘((X . Y) A CAR (N B) (X Y Z)))
Последние две строки содержат тесты. Их значения четыре и пять, соответственно. Prog-форма имеет структуру, подобную определениям функций и процедур в Паскале: (PROG, список рабочих переменных , последовательность операторов и атомов ...) Атом в списке является меткой, локализующей оператор, расположенный вслед за ним. В приведенном примере метка A локализует оператор, начинающийся с COND.
Первый список после символа PROG называется списком рабочими переменных. При отсутствии таковых должно быть написано NIL или (). С рабочими переменными обращаются примерно как со связанными переменными, но они не могут быть связаны ни с какими значениями через lambda.
Значение каждой рабочей переменной есть NIL, до тех пор, пока ей не будет присвоено что-нибудь другое.
Для присваивания рабочей переменной применяется форма SET. Чтобы присвоить переменной pi значение 3.14 пишется (SET (QUOTE PI)3.14). SETQ подобна SET, но она еще и блокирует вычисление первого аргумента. Поэтому (SETQ PI 3.14) — запись того же присваивания. SETQ обычно удобнее. SET и SETQ могут изменять значения любых переменных из а-списка более внешних функций. Значением SET и SETQ является значение их второго аргумента.
Обычно операторы выполняются последовательно. Выполнение оператора понимается как его вычисление при текущем а-списке и отбрасывание его значения. Операторы программы часто выполняются в большей степени ради действия, чем ради значения.
GO-форма, используемая для указания перехода (GO A) указывает, что программа продолжается оператором, помеченным атомом A, причем это A может быть и из внешнего выражения prog.
Условные выражения в качестве операторов программы обладают полезными особенностями. Если ни одно из пропозициональных выражений не истинно, то вместо указания на ошибку, происходящего во всех других случаях, программа продолжается оператором, следующим за условным выражением. Это справедливо лишь для условного выражения, находящегося на верхнем уровне Prog.
RETURN — нормальный конец программы. Аргумент return вычисляется, что и является значением программы. Никакие последующие операторы не вычисляются.
Формы Go, Set, Return могут применяться как операторы лишь на верхнем уровне PROG или внутри COND, находящегося на верхнем уровне PROG.
Если программа прошла все свои операторы, она оканчивается со значением NIL.
Prog-выражение, как и другие Лисп-функции, может быть рекурсивным.
Функция REV, обращающая список и все подсписки, столь же естественно пишется с помощью рекурсивного Prog-выражения.
function rev (x: list) :List; label A, B; var y, z: list; begin
A: if null (x) then rev := y; z := cdr (x); if atom (z) then goto B; z := rev (z);
B: y := cons (z, y); x := cdr (x); goto A; end;
Функция rev обращает все уровни списка, так что rev от (A ((B C) D)) даст ((D (C B))A).
(DEFUN rev (x) (prog (y z)
A (COND ((null x)(return y))) (setq z (CDR x)) (COND ((ATOM z)(goto B))) (setq z (rev z))
B (setq y (CONS z y)) (setq x (CDR x)) (goto A) ))
Для того чтобы форма prog была полностью законна, необходима возможность дополнять а-список рабочими переменными. Кроме того, операторы этой формы требуют специального расширения языка — в него включаются формы go, set и return, не известные вне prog. Атомы, играющие роль меток, работают как указатели помеченного блока.
Кроме того, уточнен механизм условных выражений: отсутствие истинного предиката не препятствует формированию значения cond -оператора, т.к. все операторы игнорируют выработанное значение. Это позволяет считать, что значением является Nil. Такое доопределение условного выражения приглянулось и в области обычных функций, где оно часто дает компактные формулы для рекурсии по списку.
В принципе, SET и SETQ могут быть реализованы с помощью a-списка примерно так же, как и поиск значения, только с копированием связей, расположенных ранее изменяемой переменной (см. функцию assign из лекции 3). Более эффективная реализация будет описана ниже.
(DEFUN set (x y) (assign x y Alist))
Обратите внимание, что введенное таким образом присваивание работает разнообразнее, чем традиционное: обеспечена вычисляемость левой части присваивания, т.е. можно в программе вычислять имена переменных, значение которых предстоит поменять.
(setq x 'y) (set x 'NEW) (print x) (print y)
Пример 6.1.
Напечатается Y и NEW (традиционно атомы печатаются заглавными буквами).
Списки свойств атомов и структура списков
До сих пор атом рассматривался только как уникальный указатель, обеспечивающий быстрое выяснение различимости имен, названий или символов. В настоящем разделе описываются списки свойств, которые начинаются или находятся в указанных ячейках.
Каждый атом имеет список свойств. Когда атом читается (вводится) впервые, тогда для него создается пустой список свойств, который потом можно заполнять. Список свойств устроен как специальная структура, подобная записям в Паскале, но указатели в такой записи сопровождаются тэгами, символизирующими тип хранимой информации. Первый элемент этой структуры расположен по адресу, который задан в указателе. Остальные элементы доступны по этому же указателю с помощью ряда специальных функций. Элементы структуры содержат различные свойства атома. Каждое свойство помечается атомом, называемым индикатором, или расположено в фиксированном поле структуры.
В первых реализациях Лиспа все системные свойства объектов располагались по единой схеме. Перечислим некоторые из индикаторов таких свойств.
PNAME — печатное имя атома для нужд ввода-вывода.
EXPR — S-выражение, определяющее функцию с именем атом, в списке свойств которого встречается EXPR.
SUBR — функция, определенная подпрограммой на машинном языке.
APVAL — постоянное значение атома, рассматриваемого как переменная.
В списке свойств атома NIL было два индикатора, PNAME и APVAL, со значением NIL.
Более детально диаграммы списков свойств приведены в описании Lisp 1.5. [1 (не найдено)].
Здесь достаточно принять к сведению, что реализация атомарных объектов — это сложная структура данных, в свою очередь представленная списками.
С помощью функции get в форме (get x i) можно найти для атома x свойство, индикатор которого равен i.
Значением (get ‘FF ‘EXPR) будет (LAMBDA (X) (COND ... )), если определение FF было предварительно задано с помощью (defun FF (X)( COND ... ).
Свойство с его индикатором может быть вычеркнуто - удалено из списка функцией remprop в форме (remprop x i).
С середины 70-х годов возникла тенденция повышать эффективность разработкой специальных структур, отличающихся в разных реализациях.
Существуют реализации, например, muLisp, допускающие работу с представлениями атома как с обычными списками посредством функций car, cdr.
Согласно стандарту Common Lisp, глобальные значения переменных и определения функций хранятся в фиксированных полях структуры атома. Они доступны с помощью специальных функций, symbol-function и symbol-value. Список произвольных свойств можно получить с использованием функции symbol-plist. Функция remprop в Clisp удаляет лишь первое вхождение заданного свойства. Новое свойство можно ввести формой вида:
(setf (get ATOM INDICATOR ) PROPERTY )
Числа представляются в Лиспе как специальный тип атома. Атом такого типа состоит из указателя с тэгом, специфицирующим слово как число, тип этого числа и адрес собственно числа произвольной длины. В отличие от обычного атома одинаковые числа при хранении не совмещаются.
До этого момента списки рассматривались на уровне текстового ввода-вывода. В настоящем разделе анализируется кодовое представление списков внутри машины и сборщик мусора, обеспечивающий повторное использование памяти.
Список свободной памяти и сборщик мусора
В любой момент времени только часть памяти, отведенной для структур списков, действительно используется для хранения S-выражений. Остальные ячейки организованы в простой список, называемый списком свободной памяти.
Первые реализации действовали по следующей схеме [1 (не найдено)].
Определенный регистр FREE содержит информацию о первой ячейке этого списка. Когда требуется слово для формирования дополнительной структуры списка, берется первое слово списка свободной памяти, а код в регистре FREE заменяется на информацию о втором слове списка свободной памяти. Не требуется никаких программных средств для того, чтобы пользователь программировал возврат ячеек в список свободной памяти. Этот возврат происходит автоматически при пропуске программы, где бы ни исчерпался список свободной памяти. Программа, восстанавливающая память, называется "мусорщик". Любая часть структуры списка, доступная программе, рассматривается как активный список и не затрагивается мусорщиком. Активные списки доступны программе через некоторые фиксированные наборы базисных ячеек, таких как ячейки списка атомов и ячейки, вмещающие частичные результаты Лисп-выражений. Сложные структуры списков могут быть произвольной длины, но каждое активное слово должно быть подведено к базисной ячейке цепью car-cdr.
Любая ячейка, не достижимая таким образом, недоступна для программы и не активна, поэтому ее содержимое не представляет интереса. Неактивные, то есть недоступные программе ячейки восстанавливаются мусорщиком в списке свободной памяти следующим образом. Во-первых, каждая ячейка, к которой можно получить доступ через цепь car-cdr, метится установлением отрицательного знака. Где бы ни выявилось отрицательное слово в цепи во время процесса пометки, мусорщик знает, что остаток раскручиваемого списка содержит уже помеченные ячейки. Затем мусорщик предпринимает линейное выметание осовободившегося пространства, собирая ячейки с положительным знаком в новый список свободной памяти и восстанавливая исходный знак активных ячеек.
Абстрактная Лисп-машина. Система команд
Встраиваемые в ядро интерпретатора операции должны соответствовать стандартным правилам доступа к параметрам и размещения выработанного результата. Таким же правилам должен подчиняться и компилируемый код. Это позволяет формально считать равноправными встроенные и программируемые функции. Компилятор по исходному тексту программы строит код программы, эквивалентный тексту. Особенности процесса компиляции достаточно сложны даже для простых языков, поэтому характеристика результата компиляции часто задается в терминах языково-ориентированных абстрактных машин. Такой подход полезен для решения ряда технологических проблем разработки программных систем (мобильность, надежность, независимость от архитектур и т.п.).
При сравнении императивного и функционального подходов к программированию, П.Лэндин (P.J.Landin) предложил специальную абстрактную машину SECD, удобную для спецификации машинно-зависимых аспектов семантики Лиспа. Подробное описание этой машины можно найти в книгах Хендерсона и Филда-Харрисона по функциональному программированию [3, 4].
Машина SECD работает над четырьмя регистрами: стек для промежуточных результатов, контекст для размещения именованных значений, управляющая вычислениями программа, резервная память (Stack, Environment, Control list, Dump). Регистры приспособлены для хранения выражений в форме атомов или списков. Состояние машины полностью определяется содержимым этих регистров. Поэтому функционирование машины можно описать достаточно точно в терминах изменения содержимого регистров при выполнении команд, что выражается следующим образом:
s e c d => s' e' c' d' — переход от старого состояния к новому.
Для характеристики встроенных команд Лисп-интепретатора и результата компиляции программ базового Лиспа понадобятся следующие команды:
LD — ввод данного из контекста в стек;
LDC — ввод константы из программы в стек;
LDF — ввод определения функции в стек;
AP — применение функции, определение которой уже в стеке;
RTN — возврат из определения функции к вызвавшей ее программе;
SEL — ветвление в зависимости от активного (верхнего) значения стека;
JOIN — переход к общей точке после ветвления;
CAR — первый элемент из активного значения стека;
CDR — без первого элемента активное значение стека;
CONS — формирование узла по двум верхним значениям стека;
ATOM — неделимость (атомарность) верхнего элемента стека;
EQ — равенство двух верхних значений стека;
SUB1 — вычитание 1 из верхнего элемента стека;
ADD1 — прибавление 1 к верхнему элементу стека;
STOP — останов.
Стек устроен традиционно по схеме "первый пришел, последний ушел". Каждая команда абстрактной машины "знает" число используемых при ее работе элементов стека, которые она удаляет из стека и вместо них размещает выработанный результат. Исполняются команды по очереди, начиная с первой в регистре управляющей программы. Машина прекращает работу при выполнении команды "останов", которая формально характеризуется отсутствием изменений в состоянии машины:
s e (STOP ) d -> s e (STOP ) d
Следуя Хендерсону, для четкого отделения обрабатываемых элементов от остальной части списка будем использовать следующие обозначения: (x . l ) — это значит, что первый элемент списка — x, а остальные находятся в списке l.
(x y . l ) — первый элемент списка — x, второй элемент списка — y, остальные находятся в списке l и т.д. Теперь мы можем методично описать эффекты всех перечисленных выше команд.
s e(LDC q . c)d -> (q . s) e c d (a . s)e(ADD1 . c)d -> (a+1 . s) e c d (a . s)e(SUB1 . c)d -> (a-1 . s) e c d (a b . s)e(CONS . c)d -> ((a . b) . s) e c d ((a . b) . s)e(CAR . c) -> (a . s) e c d ((a . b) . s)e(CDR . c) -> (b . s) e c d (a . s)e(ATOM . c)d -> (t . s) e c d (a b . s)e(EQ . c)d -> (t . s) e c d
где t — логическое значение.
Для доступа к значениям, расположенным в контексте, можно определить специальную функцию N-th, выделяющую из списка элемент с заданным номером N в предположении, что длина списка превосходит заданный адрес.
(DEFUN N-th (n list ) (COND ((EQ n 0 )(CAR list )) (T (N-th (SUB1 n ) (CDR list ) )) ))
Продолжаем описание команд Лисп-машины.
s e (LD n . c) d -> (x . s) e c d
где x — это значение (N-th n e )
При реализации ветвлений управляющая программа соответствует следующему шаблону:
( ... SEL ( ... JOIN ) ( ... JOIN ) ... )
Ветви размещены в подсписках с завершителем JOIN, после которых следует общая часть вычислений. Для большей надежности на время выполнения ветви общая часть сохраняется в дампе — резервной памяти, а по завершении ветви — восстанавливается в регистре управляющей памяти.
(t . s) e (SEL c1 c0 . c) d -> s e ct (c . d) s e (JOIN ) (c . d) -> s e c d
где ct — это c1 или c0 в зависимости от истинностного значения t.
Организация вызова процедур требует защиты контекста от локальных изменений, происходящих при интерпретации тела определения. Для этого при вводе определения функции в стек создается специальная структура, содержащая код определения функции и копию текущего состояния контекста. До этого в стеке должны быть размещены фактические параметры процедуры. Завершается процедура командой RTN, восстанавливающей регистры и размещающей в стеке результат процедуры.
s e (LDF f . c) d -> ((f . e) . s) e c d ((f . ef) vf . s) e (AP . c) d -> NIL (vf . ef) f (s e c . d) (x) e (RTN ) (s e c . d) -> (x . s) e c d
где f — тело определения, ef — контекст в момент вызова функции, vf — фактические параметры для вызова функции, x — результат функции.
Упражнение 7.1. Программа имеет вид:
(LD 3 ADD1 LDC 128 EQ STOP)
Напишите последовательность состояний стека при работе программы и сформулируйте, что она делает.
Ответ: Данная программа проверяет, меньше ли на 1 значение, хранящееся в контексте по адресу 3, чем заданная в программе константа 128. При ее работе стек проходит следующие состояния:
NIL (3 ) (4 ) (128 4 ) (NIL )
Упражнение 7.2. Напишите управляющую программу, дающую результат, эквивалентный следующим выражениям:
(CADR e ) (EQ (CAR e) 'QUOTE ) (COND ((EQ n 0 )(CAR l )) (T (CONS (SUB1 n ) (CDR l ))) )
(Адреса значений e, n, l можно обозначить как @e, @n, @l, соответственно.)
Ответ:
( LD @e CDR CAR ) ( LD @e CAR LDC QUOTE EQ ) ( LD @n LDc 0 EQ SEL (LD @l CAR JOIN) (LD @n SUB1 LD @l CDR CONS JOIN) )
Упражнение 7.3. Напишите спецификацию команды SET, сохраняющей активное значение стека в контексте по заданному в программе адресу в предположении, что длина списка превосходит заданный адрес.
Ответ: Нужна функция, заменяющая в списке указанный старый элемент новым.
(DEFUN ASS (e n list ) (COND ((EQ n 0 )(CONS e (CDR l )) ) (T (CONS (CAR l ) (ASS e (SUB1 n ) (CDR l ) ) ) ) ) )
Тогда можно описать команду SET следующим образом:
(x . s) e (SET n . c) d -> s xne c d ``
где xne = (ASS x n e) — новое состояние контекста.
Функциональная модель процессора абстрактной машины
На этом можно было бы завершить описание реализационного минимума языка Лисп, послужившего основой для функционального программирования. Но мы рассмотрим более детально еще ряд технических аспектов, иллюстрирующих возможности функционального подхода к задачам системного программирования, включая конструирование компиляторов и моделирование парадигм программирования.
Здесь же определим общий цикл выполнения программ на SECD, что даст возможность поэкспериментировать с абстрактной машиной. Вышеописанная система команд способна выполнять результаты компиляции функциональных программ, написанных на элементарном Лисп. В следующей лекции более подробно будет описан компилятор. А пока можно поупражняться с расширениями SECD.
Объявление системы команд машины и их определения:
(defun PUT (at ind def) (setf (get at ind) def)) (put 'a 'SYM '(lambda () (setq st (cons (caar st) (cdr st))) )) (put 'd 'SYM '(lambda () (setq st (cons (cadar st) (cdr st))) )) (put 'at 'SYM '(lambda () (setq st (cons (atom (car st)) (cdr st))) )) (put 'co 'SYM'(lambda () (setq st (cons (cons (car st) (cadr st)) (cddr st))) )) (put 'equ 'SYM '(lambda () (setq st (cons eq (car st) (cadr st)) (cddr st))) )) (put 'sum 'SYM '(lambda () (setq st (cons (+ (car st) (cadr st)) (cddr st))) )) (put 'def 'SYM '(lambda () (setq st (cons (- (car st) (cadr st)) (cddr st))) )) (put 'mlt 'SYM '(lambda () (setq st (cons (* (car st) (cadr st)) (cddr st))) ))
(put 'ldc 'SYM '(lambda () ; CP — продолжение программы вслед за LDC (setq st (cons (car cp) st)) (setq cp (cdr cp)) ; CP — без константы, переданной в стек ))
; Определение интерпретатора машины
(defun secd (lambda ()(cond ((null cp) (print "?end-of-program!")) ((eq (car cp) 'STOP) (print "!normal-finish!")) ((get (car cp)'SYM) (command (car cp) (cdr cp)) (secd)) (T (print "?error-command!") (setq cp (cdr cp)) (secd)) ))) (defun command (lambda (acp dcp) (setq cp dcp) (print acp) (apply (get acp 'SYM)'()) (prsecd) (read) ))
; Вывод на экран состояния машины (defun prsecd (lambda()(prst)(prcp))) (defun prst (lambda ()(print (list "stack:=" st )))) (defun prcp (lambda ()(print (list "control:=" cp ))))
; Задание состояния машины : ; ST — стек ; CP — управляющая программа ; ENV — контекст ; DM — память для восстановления состояния (setq st '()) (setq cp '(ldc 1 ldc 2 ldc 3 mlt def ldc 4 equ stop )) (secd) (prsecd) (read) (system)
(setq st '(a ((1 2) (4 5)) 3 6 7 8 9 11 13 12 14 21 25 9 1 0)) (setq cp '(at de co at equ stop sum def mlt stop)) (prsecd) (secd) (prsecd) (setq st (cddr st)) (setq cp (cdr cp)) (prsecd) (secd) (prsecd) (system) (apply (get 'a 'SYM)'()) (prst) (setq st (cdr st)) (apply (get 'd 'SYM)'()) (prst) (setq st (cdr st)) (apply (get 'at 'SYM)'()) (prst) (setq st (cdr st)) (apply (get 'co 'SYM)'()) (prst) (apply (get 'at 'SYM)'()) (prst) (setq st (cdr st)) (setq st (cdr st)) (apply (get 'equ 'SYM)'()) (prst) (setq st (cdr st)) (apply (get 'sum 'SYM)'()) (prst) (setq st (cdr st)) (apply (get 'def 'SYM)'()) (prst) (setq st (cdr st)) (apply (get 'mlt 'SYM)'()) (prst) (setq st '(12 12 12) ) (prst) (setq st (cdr st)) (apply (get 'equ'SYM)'()) (prst) (system)

Низкоуровневое программирование. Ассемблер
П.Лэндин (P.J.Landin) предложил специальную абстрактную машину SECD, удобную для спецификации машинно-зависимых аспектов семантики Лиспа, которая будет рассмотрена ниже. А в первых Лисп-системах для реализации ядра и встроенных операций использовался специальный Лисп-ассемблер LAP, описание которого приводим в качестве иллюстрации [1]. (LAP проектировался специально для нужд компилятора, но он применялся и для низкоуровневых определений функций, а также для обработки заплат (patches). Это двухпроходной встроенный, исключительно внутренний ассемблер. Первый просмотр анализирует программу и выясняет взаимосвязи между ее частями и Лисп-системой. При ассемблировании на LAP не предусмотрено и не происходит никаких манипуляций с текстами программы в файлах. Ассемблирование кода программы выполняется в оперативной памяти во время второго просмотра, выполняющего сборку кода с установлением фактических адресов.
LAP был включен в Лисп-систему как псевдо-функция от двух аргументов. Первый аргумент — листинг программы, представленный в виде списка, второй — исходная таблица символов. Результат — окончательная таблица символов, по формату напоминающая ассоциативный список.)
Можно сказать, что первые Лисп-системы обеспечивали Лисп-интерфейс для доступа ко всем возможностям оборудования в стиле работы с ассемблером, но по форме как с обычными символьными данными.
Началом листинга ассемблерной программы является строка, сообщающая ассемблеру, с какой позиции стартовать и предстоит ли полученный в результате код программы встраивать в интерпретатор как Лисп-функцию.
По завершении работы ассемблера индикатор "Тип" будет размещен в списке свойств атома "Название" вместе со специально сконструированной структурой данных, хранящей адрес построенного кода, арность и команду для вызова этого кода как подпрограммы из Лисп-интерпретатора. Тип - это обычно SUBR или FSUBR, отражает разницу в методах обработки параметров обычными и специальными функциями.
При ассемблировании атомарных форм список свойств атома проверяется на вхождение индикаторов SUBR, FSUBR.
Формы вида ( QUOTE a) рассматриваются как литеральная величина, содержащая a. Ее адрес - результат ассемблирования. Величина защищена от выметания. Новый литерал не создается, если он совпадает с ранее построенным.
Определение операций выполняется opdefine, псевдо-функцией для введения новых команд для LAP. Она устанавливает индикатор SYM в списке свойств атома, который предстоит определить как обозначение или символ команды. Ее аргумент - список пар. Каждая пара - символ и его численное значение. Обратите внимание, что здесь пара означает не "точечная" пара, а двухэлементный список.
(OPDEFINE ( (CLA 500Q8) (TRA 2Q9) (LOAD 1000) (OVBGN 7432Q) ))
Пример 7.1.
Примеры применения ассемблера
Предикат greater наводит некоторый канонический порядок среди атомов.
(LAP ( (GREATER SUBR 2) (TLQ (* 3)) (PXA 0 0) (TRA 1 4) (CLA (QUOTE *T* ) ) (TRA 1 4) ) NIL)
Пример 7.2. Лисп-функция.
Команда TSX 6204Q должна быть вставлена после позиции 6217Q. Последняя содержит CLA 6243Q и эти команды должны быть перемещены для заплатки.
(LAP (6217Q (TRA NIL) )NIL) (LAP (NIL (CLA A) (TSX 6204Q) (TRA B) ) ( (A . 6243Q) (B . 6220Q) ) ))
Пример 7.3. Заплатка для кода программы.
CLA 500Q8)
| (OPDEFINE ( ( CLA 500Q8) (TRA 2Q9) (LOAD 1000) (OVBGN 7432Q) )) |
| Пример 7.1. |
| Закрыть окно |
| (LAP ( ( GREATER SUBR 2) (TLQ (* 3)) (PXA 0 0) (TRA 1 4) (CLA (QUOTE *T* ) ) (TRA 1 4) ) NIL) |
| Пример 7.2. Лисп-функция. |
| Закрыть окно |
| (LAP (6217Q (TRA NIL) )NIL) (LAP (NIL (CLA A) (TSX 6204Q) (TRA B) ) ( (A . 6243Q) (B . 6220Q) ) )) |
| Пример 7.3. Заплатка для кода программы. |
| Закрыть окно |