Нейрокомпьютинг и его применения в экономике и бизнесе
Целевая функция
Наглядной демонстрацией полезности нелинейного анализа главных компонент является следующий простой пример (см. рисунок 4.7).
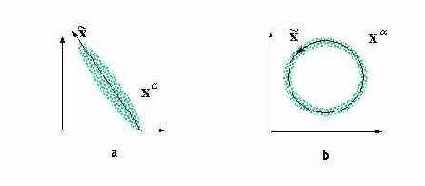
Рис. 4.7. Анализ главных компонент дает линейное подпространство, минимизирующее отклонение данных (a). Он не способен, однако, выявить одномерный характер распределения данных в случае (b). Для их одномерной параметризации нужны нелинейные координаты
Он показывает, что в общем случае нас интересует нелинейное преобразование




