Нелинейная значимость входов. Box-counting алгоритмы

Алгортимы box-counting, как следует из самого их названия, основаны на подсчете чисел заполнения примерами

ячеек (boxes), на которые специально для этого разбивается пространство переменных . Эти числа заполнения используются для оценки плотности вероятности распределения примеров по ячейкам. Набор вероятностей дает возможность рассчитать любую статистическую характеристику набора данных обучающей выборки.

Для определения значимости входов нам потребуется оценить предсказуемость выходов, обеспечиваемую данным набором входных переменных. Чем выше эта предсказуемость - тем лучше соответствующий набор входов. Таким образом, метод box-counting предоставляет в наше распоряжение технологию отбора наиболее значимых признаков для нейросетевого моделирования, технологию оптимизации входного пространства признаков.

Согласно общим положениям теории информации, мерой предсказуемости случайной величины

является ее энтропия, , определяемая как среднее значение ее логарифма. В методике box-counting энтропия приближенно оценивается по набору чисел заполнения ячеек, на которые разбивается интервал ее возможных значений: . Качественно, энтропия есть логарифм эффективного числа заполненных ячеек (см. рисунок 7.13). Чем больше энтропия переменной, тем менее предсказуемо ее значение. Когда все значения примеров сосредоточены в одной ячейке - их энтропия равна нулю, т.к. положение данных определено (с данной степенью точности). Равномерному заполнению ячеек соответствует максимальная энтропия - наибольший разброс возможных значений переменной.

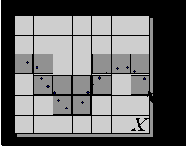
Рис. 7.13.  Смысл энтропии - эффективное число заполненных данными ячеек

Предсказуемость случайного вектора

, обеспечиваемое знанием другой случайной величины , дается кросс-энтропией:

Качественно, кросс-энтропия равна логарифму отношения типичного разброса значений переменной

к типичному разбросу этой переменной, но при известном значении переменной (см. рисунок 7.14):

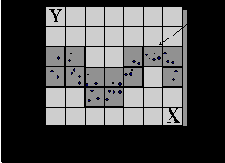
Рис. 7.14.  Иллюстрация к понятию кросс-энтропии: - полное число ячеек в объединенном пространстве , - число проекций ячеек на пространство , - характерный разброс по оси при фиксированном , - характерный разброс всех данных по jcb

Чем больше кросс-энтропия, тем больше определенности вносит знание значения в предсказание значения переменной .

Описанный выше энтропийный анализ не использует никаких предположений о характере зависимости между входными и выходными переменными. Таким образом, данная методика дает наиболее общий рецепт определения значимости входов, позволяя также оценивать степень предсказуемости выходов.

В принципе, качество предсказаний и, соответственно, значимость входной информации определяется, в конечном итоге, в результате обучения нейросети, которая, к тому же, дает решение в явном виде. Однако, как мы знаем, обучение нейросети - довольно сложная вычислительная задача (требующая операций). Между тем, существуют эффективные алгоритмы быстрого подсчета кросс-энтропии (с вычислительной сложностью ), намного более экономные, чем обучение нейросетей. Значение методики box-counting состоит в том, что не находя самого решения, она позволяет быстро предсказать качество этого прогноза. Поэтому эта методика может быть положена в основу предварительного отбора входной информации на этапе предобработки данных.




Чем больше кросс-энтропия, тем больше определенности вносит знание значения в предсказание значения переменной .

Описанный выше энтропийный анализ не использует никаких предположений о характере зависимости между входными и выходными переменными. Таким образом, данная методика дает наиболее общий рецепт определения значимости входов, позволяя также оценивать степень предсказуемости выходов.

В принципе, качество предсказаний и, соответственно, значимость входной информации определяется, в конечном итоге, в результате обучения нейросети, которая, к тому же, дает решение в явном виде. Однако, как мы знаем, обучение нейросети - довольно сложная вычислительная задача (требующая операций). Между тем, существуют эффективные алгоритмы быстрого подсчета кросс-энтропии (с вычислительной сложностью ), намного более экономные, чем обучение нейросетей. Значение методики box-counting состоит в том, что не находя самого решения, она позволяет быстро предсказать качество этого прогноза. Поэтому эта методика может быть положена в основу предварительного отбора входной информации на этапе предобработки данных.


Содержание раздела

---

---

---

Главная сайта

---