Нейрокомпьютинг и его применения в экономике и бизнесе
Нелинейное сжатие информации - карты Кохонена
Итак, линейная статистическая обработка данных не способна выделить два ведущих параметра, описывающих финансовое состояние российских банков с приемлемой точностью. В этой ситуации естественно обратиться к нелинейному статистическому анализу, т.е. к нейросетевому моделированию.
Напомним, что методом, дающим оптимальное представление информации в виде координат двумерной сетки, является построение топографических карт (карт Кохонена), о которых шла речь в лекции 4. Напомним в двух словах суть этой методики. В многомерное пространство данных погружается двумерная сетка. Эта сетка изменяет свою форму таким образом, чтобы по возможности точнее аппроксимировать облако данных. Каждой точке данных ставится в соответствие ближайший к ней узел сетки. Таким образом каждая точка данных получает некоторую координату на сетке. Такое отображение локально непрерывно: близким точкам на карте соответствуют близкие точки в исходном пространстве (обратное, вообще говоря, не верно: близким точкам в исходном пространстве могут соответствовать далекие точки на карте - такова цена понижения размерности). Таким образом, распределение данных на двумерной карте позволяет судить о локальной структуре многомерных данных.
Синаптические веса нейрона в сети Кохонена являются его координатами в исходном многомерном пространстве. Обучение сети, т.е. нахождение положения узлов карты в многомерном пространстве происходит в режиме "победитель забирает все". Данные по очереди подаются на входы всех нейронов и для каждого входа определяется ближайший к нему нейрон. Обучение состоит в подгонке весов нейрона-победителя и его ближайших соседей минимизурующих отклонение данных от нейронов-победителей. Постепенно сеть находит равновесное положение, оптимально аппроксимирующее данные (см. рисунок 10.6).
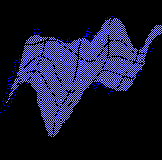
Рис. 10.6. Нелинейная аппроксимация массива многомерных данных двумерной поверхностью
Если линейный статистический анализ пытается аппроксимировать данные плоскостью, то нелинейный - использует для этих целей двумерную поверхность, что позволяет, в принципе, добиться гораздо более высокой точности аппроксимации.
Так, в нашем случае, суммарное расстояние от данных до ближайших к ним узлов топографической сетки

составляет всего


Таким образом, можно с приемлемой точностью описать финансовое состояние российских банков используя всего лишь два обобщенных финансовых индикатора, а именно - две координаты на двумерной карте Кохонена. Каждый банк по состоянию своего баллансового отчета отображается конкретной ячейкой на карте. Ячейки с одинаковыми координатами содержат банки со сходным финансовым состоянием. Чем дальше на карте координаты банков, тем больше отличается друг от друга их финансовый портрет.
Рис. 10.7. Пример содержимого ячейки Т9 карты Кохонена для российских банков (регистрационные номера и названия банков)
Так, например, рисунок 10.7 иллюстрирует содержимое конкретной ячейки на карте Кохонена российских банков, содержащей 20x20 ячеек (т.е. 400 нейронов).