Формирование списка отдельных точек функции

Шаг 1

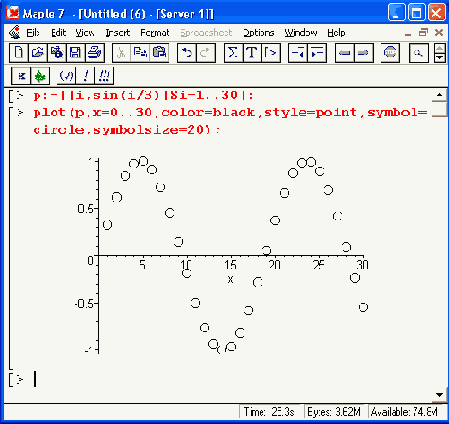
Рисунок 11.7. Формирование списка отдельных точек функции и их построение на графике

Шаг 1

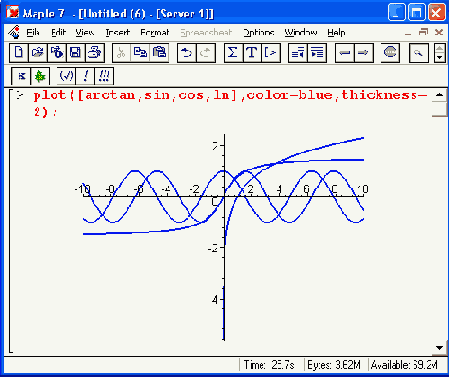
Рисунок 11.9. Построение графиков четырех функций, заданных только их именами
Этот пример показывает, что возможно построение графиков функций даже без указания в команде plot диапазонов. При этом диапазон по горизонтальной оси устанавливается равным по умолчанию -10.. 10, а по вертикальной оси выбирается автоматически в соответствии с экстремальными значениями функций в указанном диапазоне изменения независимой переменной (условно х).

Шаг 1

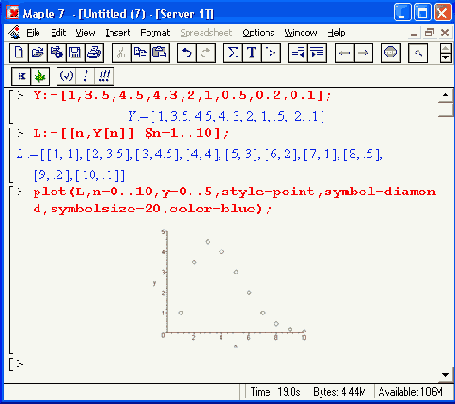
Рисунок 11.10. Построение графика точек с ординатами, заданными элементами вектора
Из этого примера нетрудно заметить, что данная задача решается составлением списка парных значений координат исходных точек — к значениям ординат точек, взятых из вектора, добавляются значения абсцисс. Они задаются чисто условно, поскольку никакой информации об абсциссах точек в исходном векторе нет, так что фактически строится график зависимости ординат точек от их порядкового номера n.

Шаг 1

Шаг 1

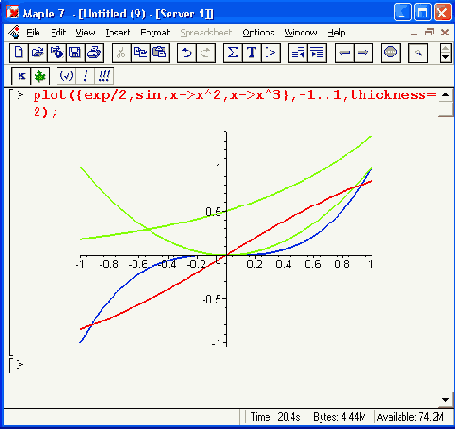
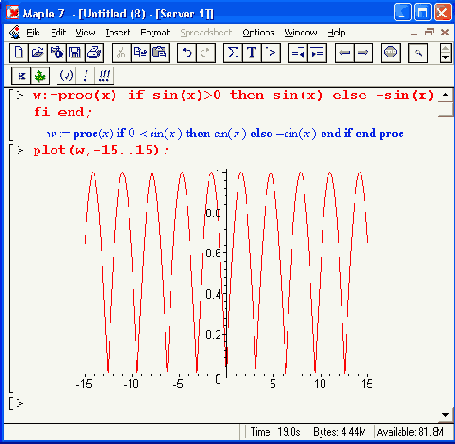
Рисунок 11.12. Построение графиков функции, заданной функциональными операторами

plot([fl(t),f2(t),t-tmin..tmax].h,v.p)
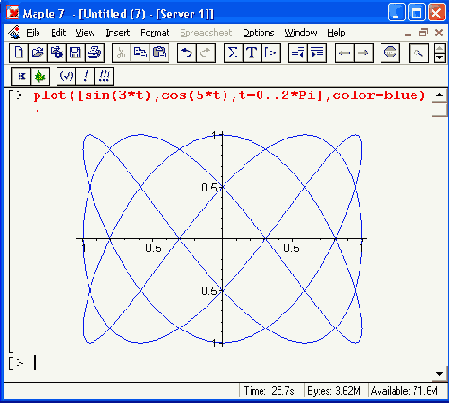
Если функции f1(£) и f2(0 содержат периодические функции (например, тригонометрические), то для получения замкнутых фигур диапазон изменения переменной t обычно задается равным 0. .2*Pi или -Pi..Pi. К примеру, если задать в качестве функций f1(t) и f2(t) функции sin(t) и cos(t), то будет получен график окружности. Рисунок 11.13 показывает другие, чуть менее тривиальные примеры построения графиков такого рода.
Задание диапазонов для изменений h и v, а также параметров р не обязательно. Но, как и ранее, они позволяют получить вид графика, удовлетворяющий всем требованиям пользователя.

Шаг 1

а

Шаг 1

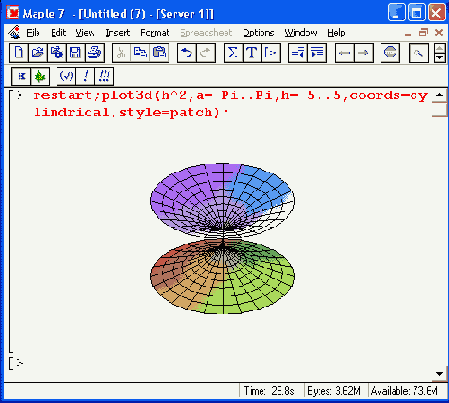
Рисунок 11.16. Нелинейная цилиндрическая поверхность
При построении этой фигуры также использована цветная функциональная окраска. Кроме того, этот пример иллюстрирует вывод над рисунком титульной надписи (кстати, сделанной на русском языке).
Приведем еще один пример построения трехмерной поверхности — на этот раз . в сферической системе координат (Рисунок 11.17). Здесь функция задана вообще элементарно просто — в виде числа 1. Но, поскольку выбрана сферическая система координат, в результате строится поверхность шара единичного радиуса.
О том, насколько необычным может быть график той или иной функции в различных системах координат, свидетельствует Рисунок 11.18. На нем показан график параметрически заданной функции от одной координаты t = sin(t3), построенный в сферической системе координат.
Кстати, Рисунок 11.18 иллюстрирует возможность одновременного наблюдения нескольких окон. В одном окне задано построение графика, а в другом построен сам график. При построении графика в отдельном окне появляется панель форматирования графика. С помощью ее довольно наглядных кнопок можно легко скорректировать вспомогательные параметры графика (окраску, наличие линий каркаса, ориентацию и др.).

Шаг 1

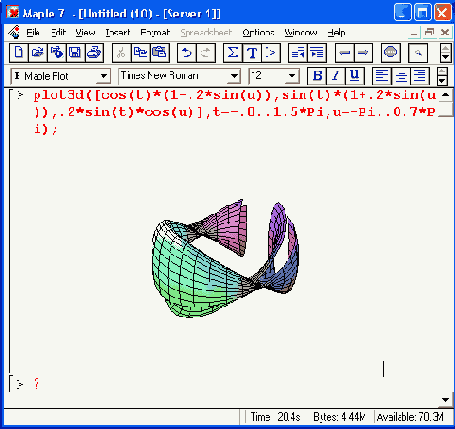
Рисунок 11.19. График трехмерной поверхности при полном параметрическом ее задании
В данном случае функциональная окраска задана из меню, поэтому в состав функции соответствующий параметр не введен. Обратите внимание на технику удаления частей фигуры путем задания соответствующего диапазона изменения параметров t и n.
Следующий пример показывает построение простого тороида — цилиндра, свернутого в кольцо (Рисунок 11.20). Здесь также использован прием удаления части фигуры, что делает ее представление более наглядным и красочным. Кроме того, введены параметры, задающие функциональную окраску.
Тор на Рисунок 11.20 выглядит, как произведение искусства. Он дает полное и наглядное представление об этой фигуре.

Шаг 1

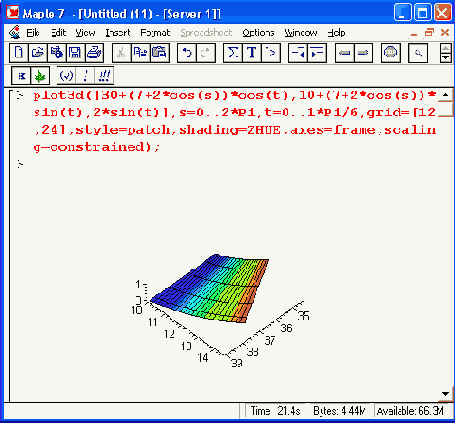
Рисунок 11.20. Тор с функциональной окраской поверхности
Задание параметра scaling= unconstrained означает отказ от равного масштаба по осям. График при этом увеличивается в размерах, но становятся заметны его искажения по осям координат. В итоге тор превращается в толстую сплющенную трубу с эллиптическим сечением (Рисунок 11.21).
Весьма важным является учет углов, под которыми наблюдается трехмерная поверхность или объект. К примеру, построение Рисунок 11.21 неудачно в том плане, что оно не показывает наличия у тора дырки. В общем, как в поговорке: «кому бублик, а кому дырка от бублика» — ведь бублик и есть материально реализованный тор. Простейший и очень удобный способ изменить угол обзора заключается во вращении фигуры на рисунке мышью при нажатой левой кнопке. При этом можно повернуть фигуру так, что ее геометрические особенности будут видны (Рисунок 11.22).
В Maple есть способ явно задать углы обзора с помощью параметра orientation=[theta, phi], где theta и phi — углы, через которые задаются параметрические уравнения трехмерной фигуры или поверхности. Рисунок 11.23 дает пример такого задания фигуры, которую можно назвать «квадратным» тором. Обратите внимание, что значения заданных углов обзора повторяются в полях углов на контекстной панели инструментов. Разумеется, последние будут меняться, если начать вращать фигуру на рисунке мышью.

Шаг 1

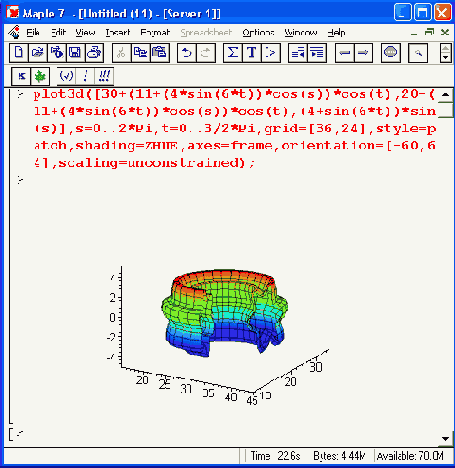
Рисунок 11.24. Тор с сечением в виде шестиконечной звезды

Шаг 1

а

Шаг 1

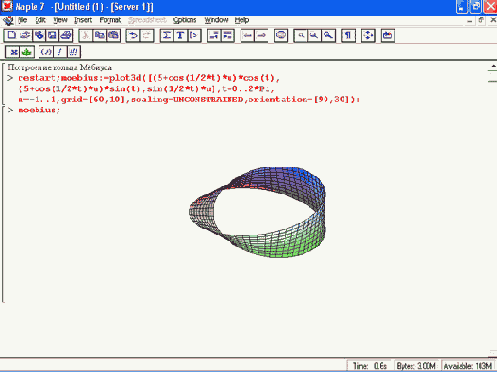
Рисунок 11.28. Пример задания и вывода трехмерного графика — графического объекта
В данном случае строится лента Мебиуса, свойства которой (например, плавный переход с одной стороны ленты на другую) уже много веков будоражат воображение людей.
Поскольку можно говорить, что вызов переменной возвращает графический объект, то это дает повод считать plot и plot3d графическими функциями.

Шаг 1

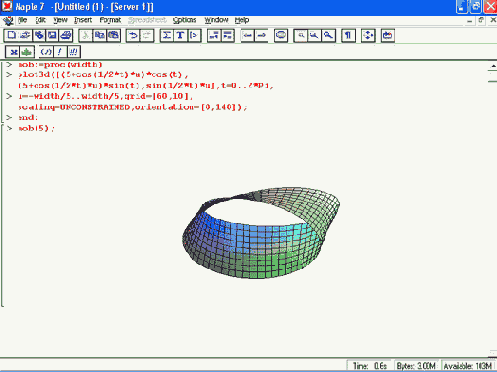
Рисунок 11.29. Пример создания и применения процедуры трехмерной графики
Этот пример показывает еще один способ задания и построения кольца Мебиуса. Практически любые графические построения можно оформлять в виде процедур и использовать такие процедуры в своих документах.

Шаг 1

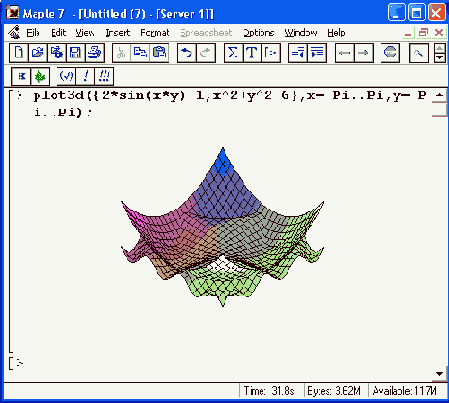
Рисунок 11.30. Пример построения двух трехмерных фигур, пересекающихся в пространстве

Шаг 1

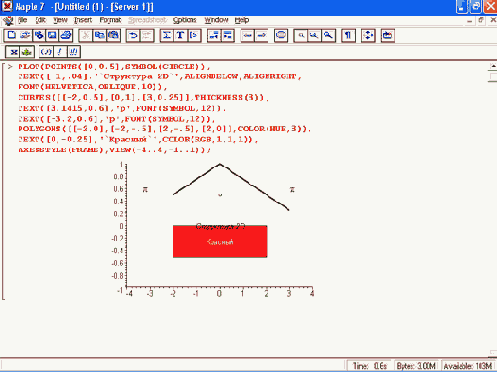
Рисунок 11.31. Пример использования двумерных структур

Шаг 1

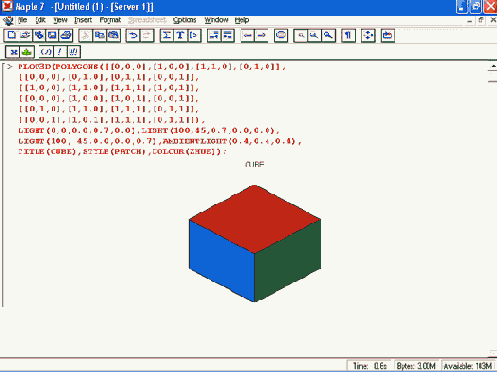
Рисунок 11.32. Пример создания структуры трехмерной графики

Шаг 1

a

Шаг 1

а

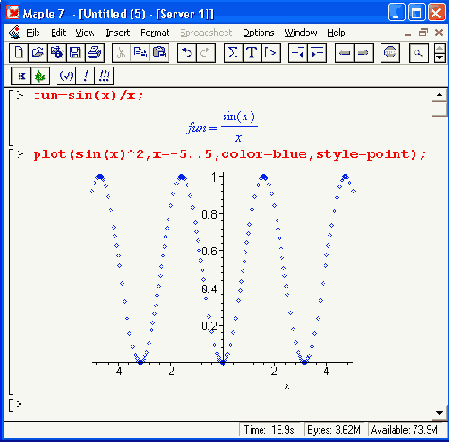
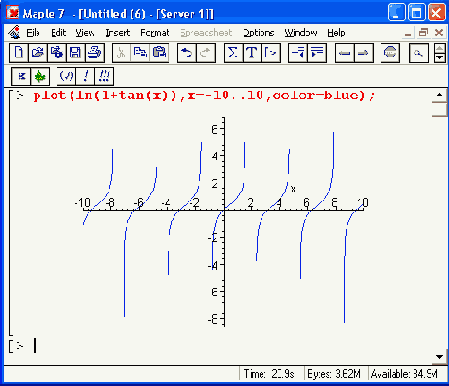
Шаг 1

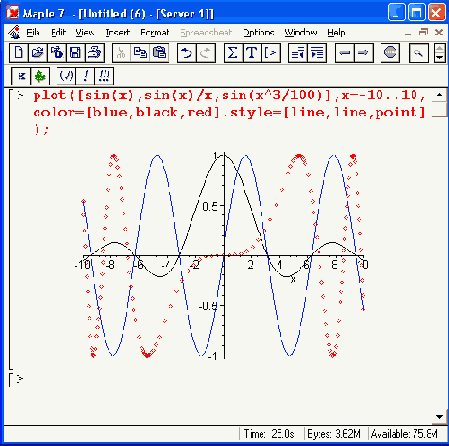
Рисунок 11.4. Графики трех функций на одном рисунке
Обычно графики разных функций автоматически строятся разными цветами. Но это не всегда удовлетворяет пользователя — например, при распечатке графиков монохромным принтером некоторые кривые могут выглядеть слишком блеклыми или даже не пропечататься вообще. Используя списки параметров color (цвет линий) и style (стиль линий), можно добиться выразительного выделения кривых — это показывает второй пример на Рисунок 11.4 для случая, когда линии графиков выделяются стилем. Однако если кривые задаются разным цветом, то при черно-белой печати они могут перестать различаться.
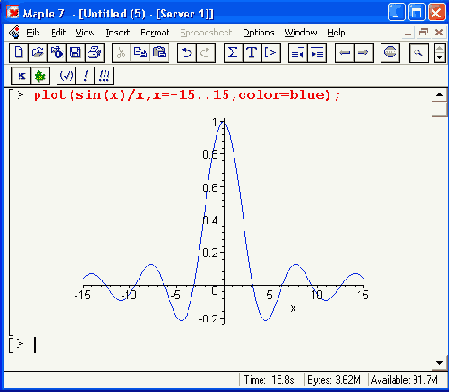
На Рисунок 11.5 показан еще один пример такого рода. Здесь построен график функции sin(x)/x и график ее полиномиальной аппроксимации. Она выполняется настолько просто, что соответствующие функции записаны прямо в списке параметров функции plot.

Шаг 2

а

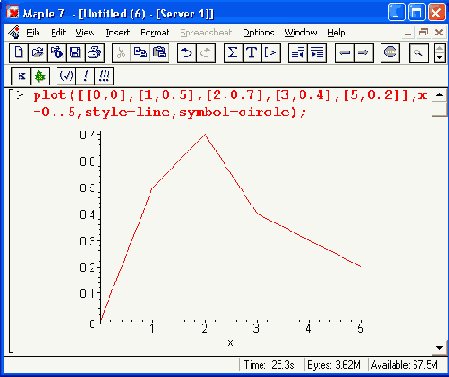
Шаг 2

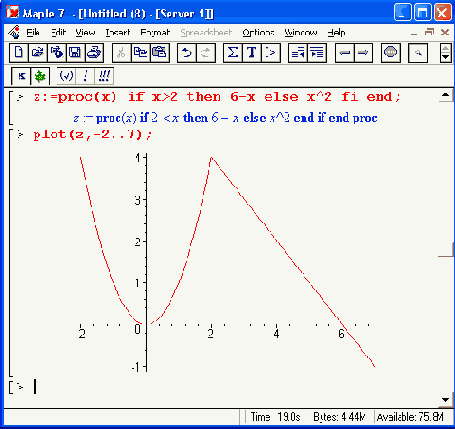
Рисунок 11.11. Построение графика функций, заданных процедурами
Здесь, пожалуй, полезно обратить внимание на то, что в функции plot указывается имя процедуры без списка ее параметров.

Шаг 2

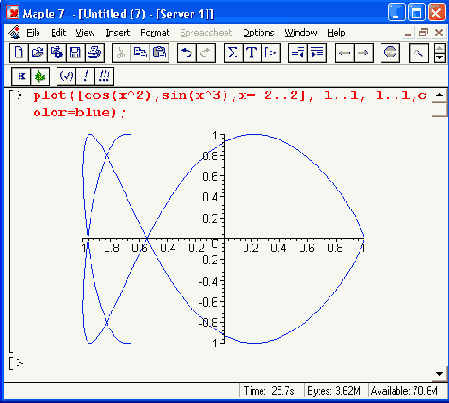
Рисунок 11.13. Построение функций, заданных параметрически
plot([r(t),theta(t),t=tmin..tnrax],h,v,p,coords-polar)
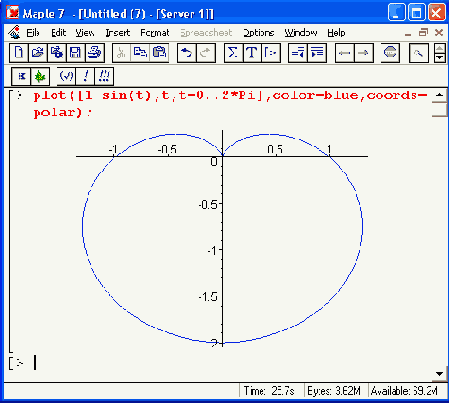
Здесь существенным моментом является задание полярной системы координат параметром coords=polar. Рисунок 11.14 дает примеры построения графиков функций в полярной системе координат.
Графики параметрических функций и функций в полярной системе координат отличаются огромным разнообразием. Снежинки и узоры мороза на стеклах, некоторые виды кристаллов и многие иные физические объекты подчиняются математическим закономерностям, положенным в основу построения таких графиков.

Шаг 2

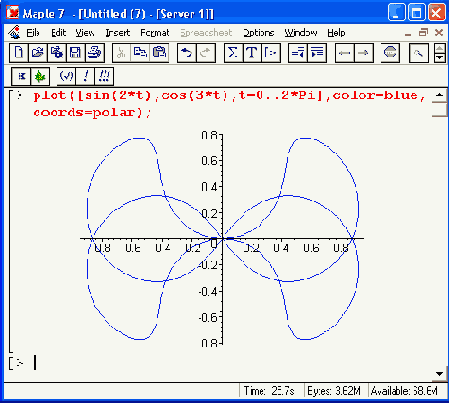
Рисунок 11.14. Построение графиков функций в полярной системе координат
Для построения графиков трехмерных поверхностей Maple имеет встроенную в ядро функцию pi ot3d. Она может использоваться в следующих форматах:
plot3d(exprl. x=a..b. y=c..d,p)
plot3d(f, a..b. c..d.p)
plot3d([exprf.exprg.exprh]. s=a..b, t=c..d.p)
plot3d([f.g.h]. a..b, c..d,p)
В двух первых формах plot3d применяется для построения обычного графика одной поверхности, в других формах — для построения графика с параметрической формой задания поверхности. В приведенных формах записи f, g и h — функции; exprl — выражение, отражающее зависимость от -х и у; exprf, exprg и exprh — выражения, задающие поверхность параметрически; s, t, а и b — числовые константы действительного типа; end — числовые константы или выражения действительного типа; х, у, s и t — имена независимых переменных; р — управляющие параметры.

Шаг 2

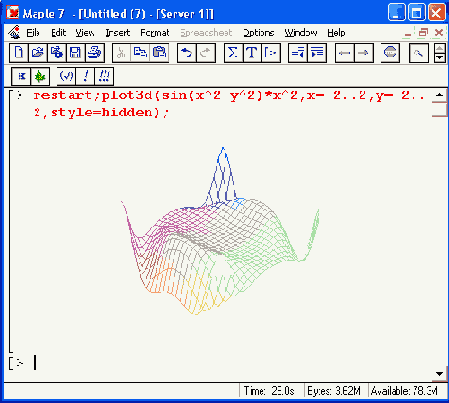
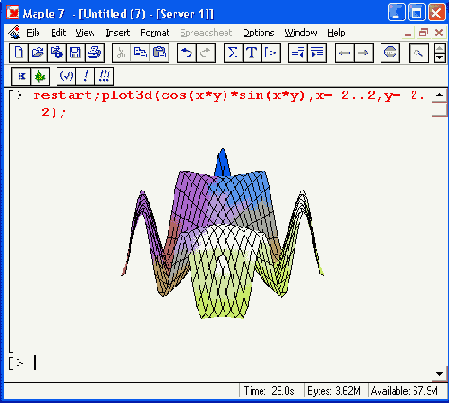
Рисунок 11.15. Примеры простейшего построения трехмерных поверхностей
Цвет трехмерного графика может задаваться (как и для двумерного) параметром соlог=с, где с — цвет (оттенки цвета перечислялись ранее). Возможно еще два алгоритма задания цвета:

HUE — алгоритм с заданием цвета в виде color=f(x,y);
RGB — алгоритм с заданием цвета в виде color=[exprr,exprg,exprb], где выражения ехрrr, ехрrg и exprb задают относительную значимость (от 0 до 1) основных цветов (красного — ехрrr, зеленого — ехрrg и синего — exprb).

Удачный выбор углов обзора фигуры и применение функциональной окраски позволяют придать построениям трехмерных фигур весьма эффектный и реалистический вид.

Шаг 2

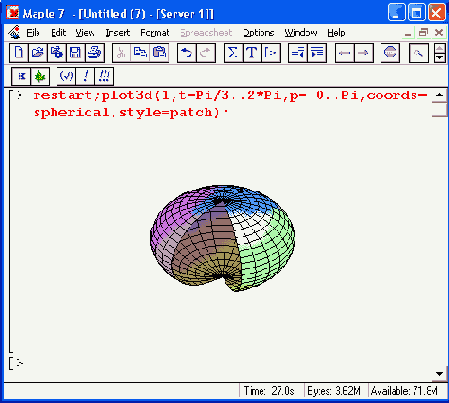
Рисунок 11.17. Построение шарообразной поверхности в сферической системе координат

Шаг 2

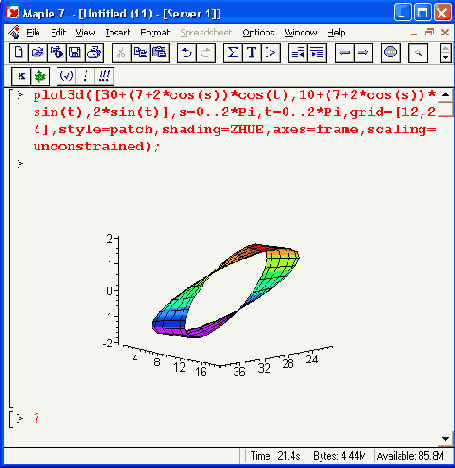
Рисунок 11.21. Тор, построенный с применением значения параметра seating-unconstrained

Шаг 2

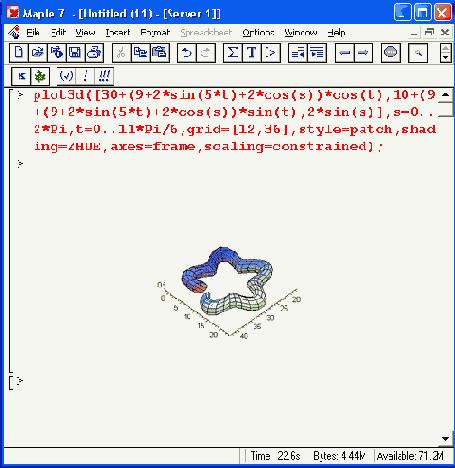
Рисунок 11.25. Тор круглого сечения в виде пятиконечной звезды

Шаг 2

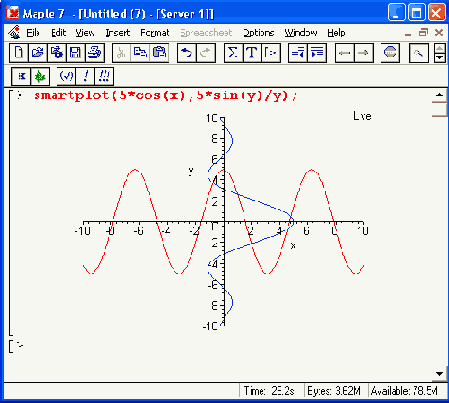
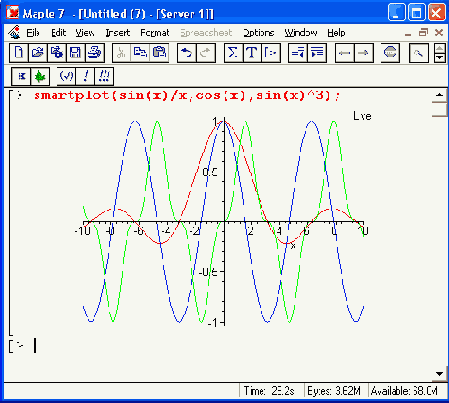
Рисунок 11.26. Построение графиков с помощью функции smartplot
Обратите внимание на второй пример применения функции smartplot. Здесь график выражения 5sin(y)/y построен относительно вертикальной оси. Поэтому он развернут на 90° относительно графика, построенного обычным образом.
Примечание 1
Примечание 1

На графиках, построенных командой smartplot(x), присутствует надпись «Live», что — видно на Рисунок 11.26.

Шаг 2

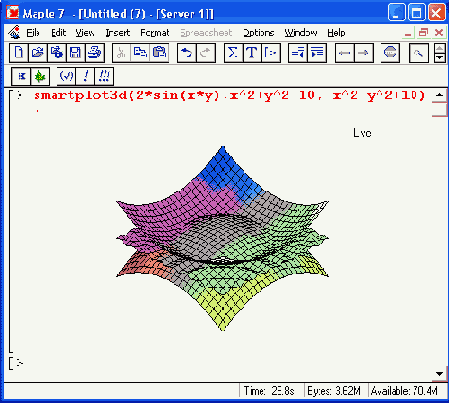
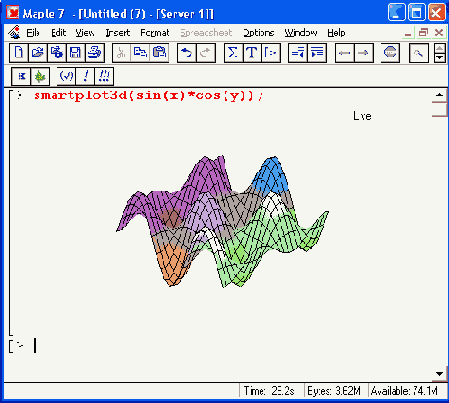
Рисунок 11.27. Примеры применения функции smartplot3d
Как видно из второго примера, представленного на Рисунок 11.27, функция smartplot3d обеспечивает построение не только отдельных поверхностей, но и ряда Пересе, кающихся поверхностей. При этом линии пересечения поверхностей строятся вполне корректно.

Шаг 2

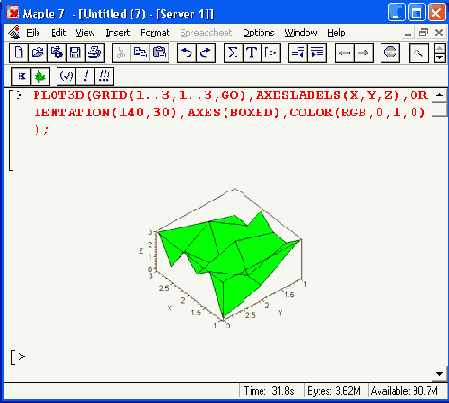
Рисунок 11.33. Пример задания графической структуры типа GRID
Обычная форма задания этой структуры следующая:
MESH([[[x11,y11,z11]....[x1n,y1n,z1n]]. [[x21,y21,z21]....[x2n,y2n,z2n]]. ...[[xm1,ym1,zm1]...[xmn,ymn,zmn]]])
Пример задания такой структуры представлен на Рисунок 11.34.

Шаг 2

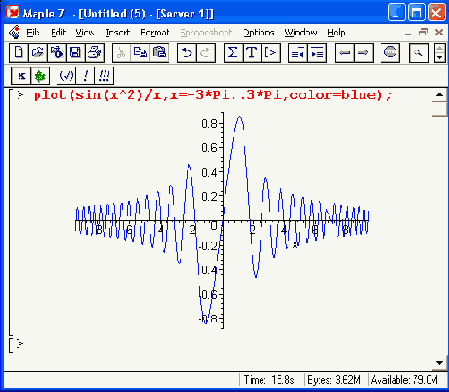
Рисунок 11.1. Примеры построения графиков одной функции
При построении графиков одной функции могут быть введены описание диапазонов и различные параметры, например: для задания цвета кривой, толщины линии, которой строится график функции, и др. К примеру, запись в списке параметров color=black задает вывод кривых черным цветом, а запись thikness=2 задает во втором примере Рисунок 11.1 построение графика линией, удвоенной по сравнению с обычной толщиной. Кстати говоря, запись color=red дает красный цвет, color=green — зеленый цвет, color=blue — синий цвет и т. д. При черно-белой печати цвета представляются оттенками серого цвета.

Шаг 2

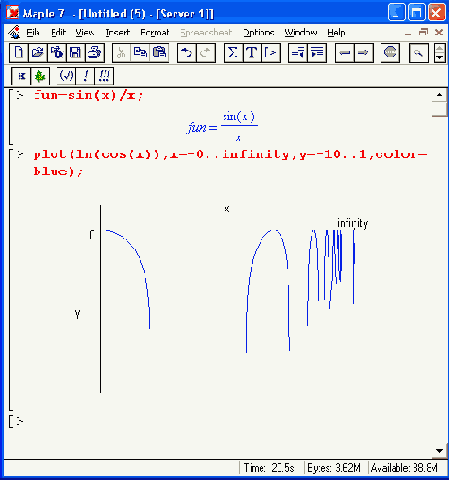
Рисунок 11.2. Построение графиков функции с явным указанием масштаба
Правильный выбор диапазонов повышает представительность графиков функций. Рекомендуется вначале пробовать строить графики с автоматическим выбором диапазонов, а уже затем указывать их вручную.

Шаг 2

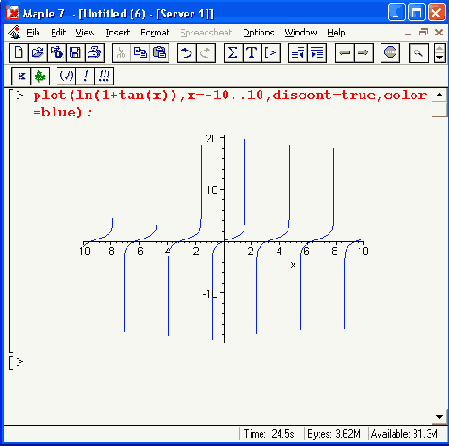
Рисунок 11.3. Построение графиков функций с разрывами

Шаг 2

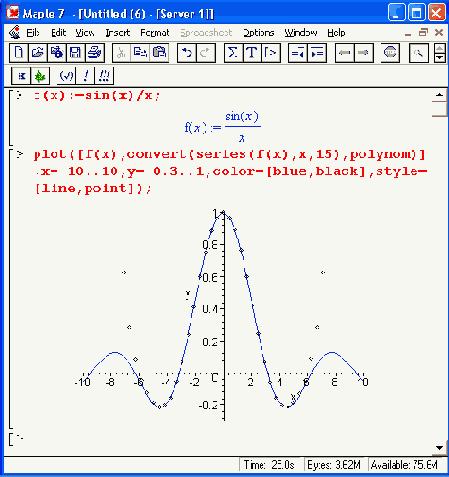
Рисунок 11.5. График функции sin(x)/x и ее полиномиальной аппроксимации
В данном случае сама функция построена сплошной линией, а график полинома точками — ромбами. Хорошо видно, что при малых х аппроксимация дает высокую точность, но затем с ростом х ее погрешность резко возрастает.
Рисунок 11.6 показывает построение нескольких любопытных функций, полученных с помощью комбинаций элементарных функций. Такие комбинации позволяют получать периодические функции, моделирующие сигналы стандартного вида: в виде напряжения на выходе двухполупериодного выпрямителя, симметричных прямоугольных колебаний (меандр), пилообразных и треугольных импульсов, треугольных импульсов со скругленной вершиной.

Шаг 3

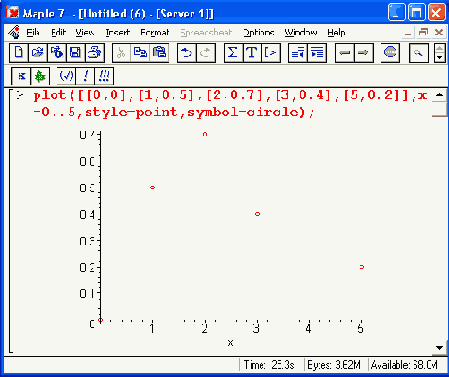
Рисунок 11.8. Построение графика функции, явно заданной отдельными точками
Во втором примере Рисунок 11.8 показано построение только точек заданной функциональной зависимости. Они представлены маленькими кружками. Читателю предлагается самостоятельно совместить оба подхода к построению графиков по точкам и создать график в виде отрезков прямых, соединяющих заданные точки функции, представленные кружками или крестиками.

Шаг 3

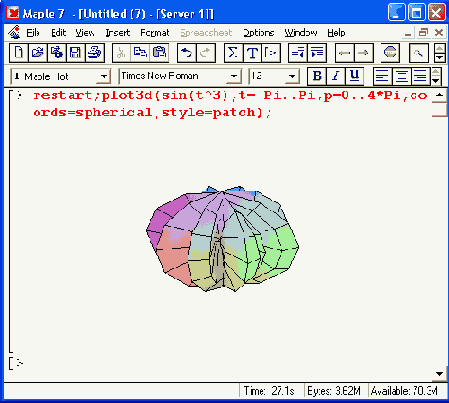
Рисунок 11.18. График еще одной поверхности в сферической системе координат

Шаг 3

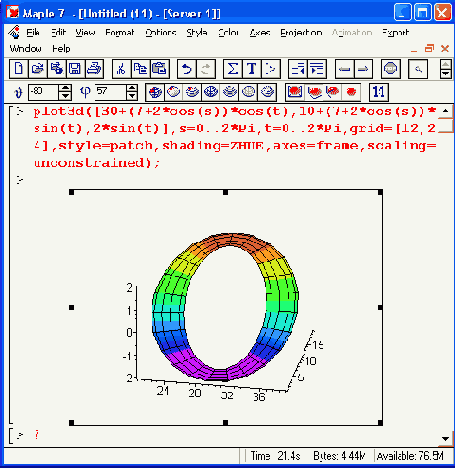
Рисунок 11.22. Тор с Рисунок 11. 21 после поворота мышью демонстрирует, что он и впрямь имеет дырку

Шаг 3

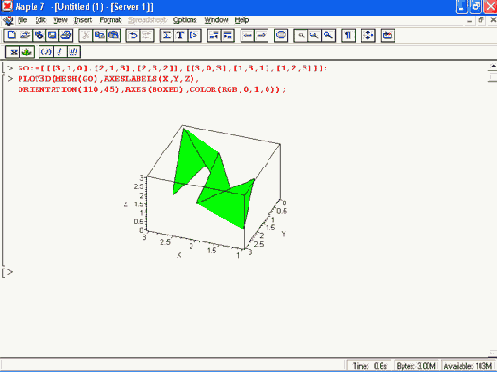
Рисунок 11.34. Пример задания графической структуры типа MESH
Описанные структуры могут использоваться и в программных модулях. Много таких примеров описано в книгах, поставляемых с системой Maple 7.

Шаг 3

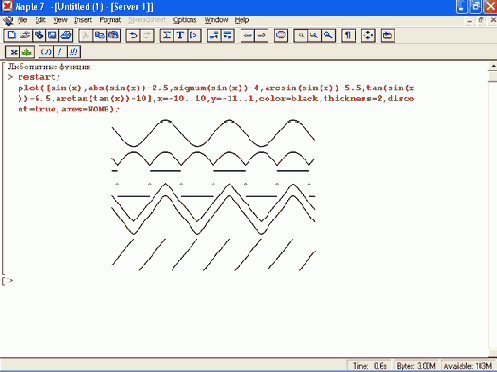
Рисунок 11.6. Построение графиков нескольких любопытных функций
В этом рисунке запись axes=NONE убирает координатные оси. Обратите внимание, что смещение графиков отдельных функций вниз с целью устранения их наложения достигнуто просто прибавлением к значению каждой функции некоторой константы.

Шаг 4

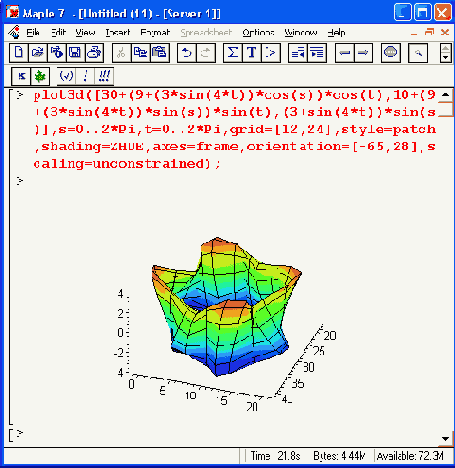
Рисунок 11.23. «Квадратный» тор, представленный под заданными углами обзора

Содержание раздела